Chapter: Artificial Intelligence
Various Types of Artificial Intelligence Problems and their Solutions
VARIOUS TYPES OF PROBLEMS AND
THEIR SOLUTIONS
1.
Water Jug Problem,
2.
Missionaries and Carnivals Problem,
3.
Chess Problem,
4.
8- Queen Problem,
5.
8- Puzzle Problem,
6.
Monkey Banana Problem,
7.
Tower of Hanoi Problem,
8.
Cryptarithmatic Problem.
Water Jug Problem
Definition:
Some jugs are given which should have non-calibrated properties. At
least any one of the jugs should have filled with water. Then the process
through which we can divide the whole water into different jugs according to
the question can be called as water jug problem.
Procedure:
Suppose that you are given 3 jugs A,B,C with capacities 8,5 and 3 liters
respectively but are not calibrated (i.e. no measuring mark will be there). Jug
A is filled with 8 liters of water. By a series of pouring back and forth among
the 3 jugs, divide the 8 liters into 2 equal parts i.e. 4 liters in jug A and 4
liters in jug B. How?
In this problem, the start state is that the jug A will contain 8 liters
water whereas jug B and jug C will be empty. The production rules involve
filling a jug with some amount of water, taking from the jug A. The search will
be finding the sequence of production rules which transform the initial state
to final state. The state space for this problem can be described by set of
ordered pairs of three variables (A, B, C) where variable A represents the 8
liter jug, variable B represents the 5 liter and variable C represents the 3
liters jug respectively.

The production rules are formulated as follows:
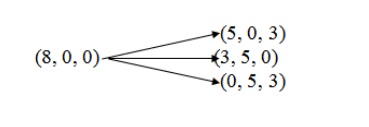
Step 1:
In this step, the initial state will be (8, 0, 0) as the jug B and jug C
will be empty. So the water of jug A can be poured like:
(5, 0, 3) means 3 liters to jug C and 5 liters will remain in jug A.
(3, 5, 0) means 5 liters to jug B and 3 liters will be in jug A.
(0, 5, 3) means 5 liters to jug B and 3 liters to jug C and jug C and
jug A will be empty.
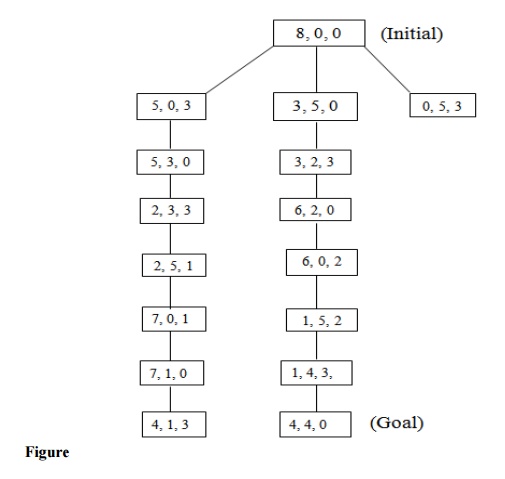
Step2:
In this step, start with the first current state of step-1 i.e. (5, 0,
3). This state can only be implemented by pouring the 3 liters water of jug C
into jug B. so the state will be (5, 3, 0). Next, come to the second current
state of step-1 i.e. (3, 5, 0). This state can be implemented by only pouring
the 5 liters water of jug B into jug C. So the remaining water in jug B will be
2 liters. So the state will be (3, 2, 3). Finally come to the third current
state of step-1 i.e. (0, 5, 3). But from this state no more state can be
implemented because after implementing we may get (5, 0, 3) or (3, 5, 0) or (8,
0, 0) which are repeated state. Hence these states are not considerably again
for going towards goal.
So the state will be like:


So finally the state will be (4, 4, 0) that means jug A and jug B
contains 4 liters of water each which is our goal state. One thing you have to
very careful about the pouring of water from one jug to another that the
capacity of jug must satisfy the condition to contain that much of water.
The tree of the water jug problem can be like:
Comments:
This problem takes a lot of time to find the goal
state.
This process of searching in this problem is very lengthy.
At each step of the problem the user have to
strictly follow the production rules. Otherwise the problem may go to infinity
step.
Missionaries and Carnivals
Problem
Definition:
In Missionaries and Carnivals Problem, initially there are some
missionaries and some carnivals will be at a sideof a river. They want to cross
the river. But there is only one boat available to cross the river. The
capacity of the boat is 2 and no one missionary or no Carnivals can cross the
river together. So for solving the problem and to find out the solution on
different states is called the Missionaries and Carnival Problem.
Procedure:
Let us take an example. Initially a boatman, Grass, Tiger and Goat is
present at the left bank of the river and want to cross it. The only boat
available is one capable of carrying 2 objects of portions at a time. The
condition of safe crossing is that at no time the tiger present with goat, the
goat present with the grass at the either side of the river. How they will
cross the river?
The objective of the solution is to find the sequence of their transfer
from one bank of the river to the other using the boat sailing through the
river satisfying these constraints.
Let us use different representations for each of the missionaries and
Carnivals as follows.
B: Boat
T: Tiger
G: Goat
Gr: Grass
Step 1:
According to the question, this step will be (B, T, G, Gr) as all the
Missionaries and the Carnivals are at one side of the bank of the river.
Different states from this state can be implemented as
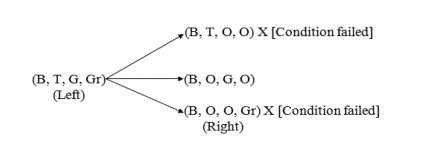
`The states (B, T, O, O) and (B, O, O, Gr) will not be countable because
at a time the Boatman and the Tiger or the Boatman and grass cannot go. (According
to the question).
Step 2:
Now consider the current state of step-1 i.e. the state (B, O, G, O).
The state is the right side of the river.
So on the left side the state may be (B, T, O, Gr)
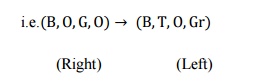
Step 3:
Now proceed according to the left and right sides of the river such that
the condition of the problem must be satisfied.
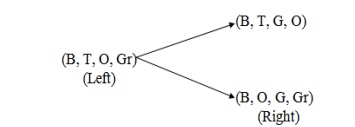
Step 4:
First, consider the first current state on the right side of step 3 i.e.


Hence the final state will be (B, T, G, Gr) which are on the right side
of the river.
Comments:
This problem requires a lot of space for its state
implementation. It takes a lot of time to search the goal node.
The production rules at each level of state are
very strict.
Chess Problem
Definition:
It is a normal chess game. In a chess problem, the start is the initial
configuration of chessboard. The final state is the any board configuration,
which is a winning position for any player. There may be multiple final
positions and each board configuration can be thought of as representing a
state of the game. Whenever any player moves any piece, it leads to different
state of game.
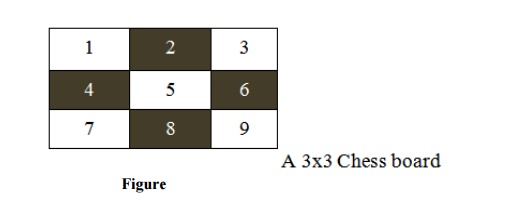
The above figure shows a 3x3 chessboard with each square labeled with
integers 1 to 9. We simply enumerate the alternative moves rather than
developing a general move operator because of the reduced size of the problem.
Using a predicate called move in predicate calculus, whose parameters are the
starting and ending squares, we have described the legal moves on the board.
For example, move (1, 8) takes the knight from the upper left-hand corner to
the middle of the bottom row. While playing Chess, a knight can move two
squares either horizontally or vertically followed by one square in an orthogonal
direction as long as it does not move off the board.
The all possible moves of figure
are as follows.
Move (1, 8) move (6, 1)
Move (1, 6) move (6, 7)
Move (2, 9) move (7, 2)
Move (2, 7) move (7, 6)
Move (3, 4) move (8, 3)
Move (3, 8) move (8, 1)
Move (4, 1) move (9, 2)
Move (4, 3) move (9, 4)
The above predicates of the Chess Problem form the knowledge base for
this problem. An unification algorithm is used to access the knowledge base.
Suppose we need to find the positions to which the knight can move from
a particular location, square 2. The goal move (z, x) unifies with two
different predicates in the knowledge base, with the substitutions {7/x} and
{9/x}. Given the goal move (2, 3), the responsible is failure, because no move
(2, 3) exists in the knowledge base.
Comments:
In this game a lots of production rules are applied
for each move of the square on the chessboard. A lots of searching are required
in this game.
Implementation of algorithm in the knowledge base
is very important.
8- Queen Problem
Definition:
ÔÇťWe have 8 queens and an 8x8 Chess board having al ternate black and
white squares. The queens are placed on the chessboard. Any queen can attack
any other queen placed on same row, or column or diagonal. We have to find the
proper placement of queens on the Chess board in such a way that no queen
attacks other queenÔÇŁ.
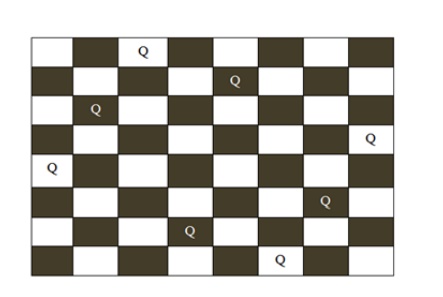
Procedure:
Figure A possible board
configuration of 8 queen problem
In figure , the possible board configuration for 8-queen problem has been
shown. The board has alternative black and white positions on it. The different
positions on the board hold the queens. The production rule for this game is
you cannot put the same queens in a same row or same column or in same
diagonal. After shifting a single queen from its position on the board, the
user have to shift other queens according to the production rule. Starting from
the first row on the board the queen of their corresponding row and column are
to be moved from their original positions to another position. Finally the
player has to be ensured that no rows or columns or diagonals of on the table
is same.
Comments:
This problem requires a lot of space to store the board.
It requires a lot of searching to reach at the goal
state. The time factor for each queenÔÇÖs move is very lengthy. The problem is
very strict towards the production rules.
8- Puzzle
Problem
Definition:
ÔÇťIt has set off a 3x3 board having 9 block spaces o ut of which 8 blocks
having tiles bearing number from 1 to 8. One space is left blank. The tile
adjacent to blank space can move into it. We have to arrange the tiles in a
sequence for getting the goal stateÔÇŁ.
Procedure:
The 8-puzzle problem belongs to the category of ÔÇťsl iding block puzzleÔÇŁ
type of problem. The 8-puzzle i s a square tray in which eight square tiles are
placed. The remaining ninth square is uncovered. Each tile in the tray has a
number on it. A tile that is adjacent to blank space can be slide into that
space. The game consists of a starting position and a specified goal position.
The goal is to transform the starting position into the goal position by
sliding the tiles around. The control mechanisms for an 8-puzzle solver must
keep track of the order in which operations are performed, so that the
operations can be undone one at a time if necessary. The objective of the
puzzles is to find a sequence of tile movements that leads from a starting
configuration to a goal configuration such as two situations given below.
Figure (Starting State) (Goal State)
The state of 8-puzzle is the different permutation of tiles within the
frame. The operations are the permissible moves up, down, left, right. Here at
each step of the problem a function f(x) will be defined

Where
g x: how many steps in the problem you have already done or the current
state from the initial state.
h x: Number of ways through which you can reach at the goal state from the
current state or
or
h x is the heuristic estimator
that compares the current state with the goal state note down how many states
are displaced from the initial or the current state. After calculating the f
(x) value at each step finally take the smallest f (x) value at every step and
choose that as the next current state to get the goal state.
Let us take an example.
Figure (Initial State) (Goal State)
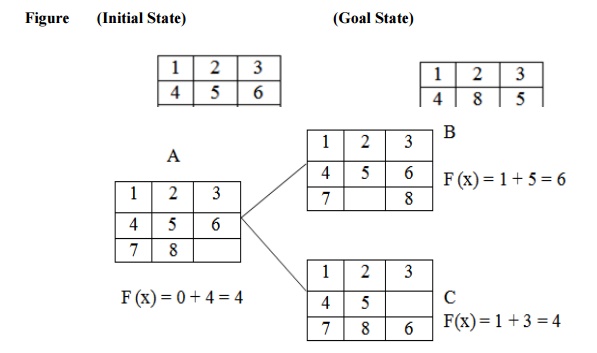
Step1:
f xis the step required to reach at the goal state from the initial state.
So in the tray either 6 or 8 can change their portions to fill the empty
position. So there will be two possible current states namely B and C. The f
(x) value of B is 6 and that of C is 4. As 4 is the minimum, so take C as the
current state to the next state.
Step 2:
In this step, from the tray C three states can be drawn. The empty
position will contain either 5 or 3 or 6. So for three different values three
different states can be obtained. Then calculate each of their f (x) and
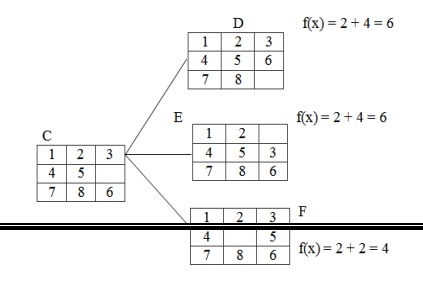
take the minimum one.
Here the state F has the minimum value i.e. 4 and hence take that as the
next current state.
Step 3:
The tray F can have 4 different states as the empty positions can be
filled with b4 values i.e.2, 4, 5, 8.
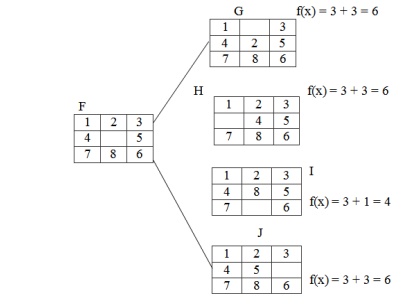
Step 4:
In the step-3 the tray I has the smallest f (n) value. The tray I can be
implemented in 3 different states because the empty position can be filled by
the members like 7, 8, 6.
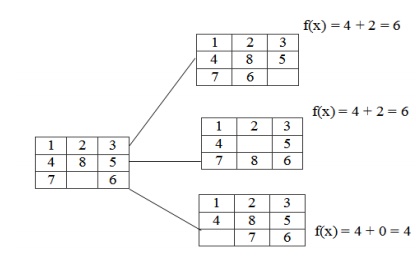
Hence, we reached at the goal state after few changes of tiles in
different positions of the trays.
Comments:
This problem requires a lot of space for saving the different trays.
Time complexity is more than that of other problems.
The user has to be very careful about the shifting
of tiles in the trays. Very complex puzzle games can be solved by this
technique.
Monkey Banana Problem
Definition:
ÔÇťA monkey is in a room. A bunch of bananas is hangi ng from the ceiling.
The monkey cannot reach the bananas directly. There is a box in the corner of
the room. How can the monkey get the bananas?ÔÇŁ
Procedure:
The solution of the problem is of course that the monkey must push the
box under the bananas, then stand on the box and grab the bananas. But the
solution procedure requires a lot of planning algorithms. The purpose of the
problem is to raise the question: Are monkeys intelligent? Both humans and
monkeys have the ability to use mental maps to remember things like where to go
to find shelter or how to avoid danger. They can also remember where to go to
gather food and water, as well as how to communicate with each other. Monkeys
have the ability not only to remember how to hunt and gather but they also have
the ability to learn new things, as is the case with the monkey and the
bananas. Even though that monkey may never have entered that room before or had
only a box for a tool to gather the food available, that monkey can learn that
it needs to move the box across the floor, position it below the bananas and
climb the box to reach for them. Some people believe that this is part
instinct, part learned behaviour. It is most probably both.
Initially, the monkey is at location ÔÇśAÔÇÖ, the banan a is at location ÔÇśBÔÇÖ
and the box is at location ÔÇśCÔÇÖ . The monkey and box have height ÔÇťlowÔÇŁ; but if
the monkey climbs onto the box will have height ÔÇťHighÔÇŁ, the same as the
bananas.
The action available to the monkey include:
ÔÇťGOÔÇŁ from one place to another.
ÔÇťPUSHÔÇŁ an object from one place to another.
ÔÇťClimbÔÇŁ onto an object.
ÔÇťGraspÔÇŁ an object.
Grasping results in holding the object if the monkey and the object are
in the same place at the same height.
The solution of the problem in different steps can be of followings.


So the solution to the planning problem may be of
following
GO(A,C)
PUSH (Box, C, B, Low)
Climb Up(Box , B)
Grasp(banana, B, High)
Climb down(Box)
Push(Box, B, C, Low)
Comments:
One major application of the monkey banana problem is the toy problem of
computer science.
One of the specialized purposes of the problem is
to raise the question: Are monkeys intelligent? This problem is very useful in
logic programming and planning.
Tower of Hanoi Problem
Definition:
ÔÇťWe are given a tower of eight discs (initially) fo ur in the applet
below, initially stacked in increasing size on one of three pegs. The objective
is to transfer the entire tower to one of the other pegs (the right most one in
the applet below), moving only one disc at a time and never a larger one onto a
smallerÔÇŁ.
Procedure:
The tower of Hanoi puzzle was invented by the French mathematician
Eduardo Lucas in 1883. The puzzle is well known to students of computer science
since it appears in virtually any introductory text on data structure and
algorithms.
The objective of the puzzle is to move the entire stack to another rod,
obeying the following rules.
Only one disc can be moved at a time.
Each move consist of taking the upper disc from one
of the rods and sliding it onto another rod, on top of the other discs that may
already be present on that rod.
No disc may be placed on the top of a smaller disk.
There is a legend about a Vietnamese temple which contains a large room
with three times. Worn posts in it surrounded by 64 golden disks. The priests
of Hanoi, acting out of command of an ancient prophecy, have been moving these
disks, in accordance with the rules of the puzzle, since that time. The puzzle
is therefore also known as the tower of Brahma puzzle. According to the legend,
when the last move of the puzzle is completed, the world will end.
There are many variations on this legend. For instance, in some
tellings, the temple is a monastery and the priests are monks. The temple or
monastery may be said to be in different parts of the world including Hanoi,
Vietnam and may be associated with any religion. The flag tower of Hanoi may
have served as the inspiration for the name.
The puzzle can be played with any number of disks, although many toy
versions have around seven to nine of them. The game seems impossible to many
novices yet is solvable with a simple algorithm. The following solution is a
very simple method to solve the tower of Hanoi problem.
Alternative moves between the smallest piece and a non- smallest piece.
When moving the smallest piece, always move it in the same direction (to the
right if starting number of pieces is even, to the left if starting number of
pieces is odd).
If there is no tower in the chosen direction, move
the pieces to the opposite end, but then continue to move in the correct
direction, for example if you started with three pieces, you would move the
smallest piece to the opposite end, then continue in the left direction after
that.
When the turn is to move the non-smallest piece,
there is only one legal move.
Doing this should complete the puzzle using the least amount of moves to
do so. Finally, the user will reach at the goal. Also various types of
solutions may be possible to solve the tower of Hanoi problem like recursive
procedure, non-recursive procedure and binary solution procedure.
Another simple solution to the problem is given below.
For an even number of disks
Make the legal move between pegs A and B. Make the
legal moves between pages A and C. Make the legal move between pages B and C.
For an even number of disks
Make the legal move between pegs A and C. Make the
legal move between pegs A and B. Make the legal move between pegs B and C.
Repeat until complete.
A recursive solution for tower of Hanoi problem is as follows.
A key to solving this problem is to recognize that it can be solve by
breaking the problem down into the collection of smaller problems and further
breaking those problems down into even smaller problems until a solution is
reached. The following procedure demonstrates this approach.
Label the pegs A, B, C - these levels may move at
different steps. Let n be the total number of disks.
Number of disks from 1 (smallest, topmost) to n
(largest, bottommost). To move n disks from peg A to peg C.
a)
Move n-1 disks from A to B. This
leaves disk #n alone on peg A.
b)
Move disk #n from A to C.
c)
Move n-1 disks from B to C so
they sit on disk #n.
To carry out steps a and c, apply the same algorithm again for n-1. The entire
procedure is a finite number of steps, since at most point the algorithm will
be required for n = 1. This step, moving a single disc from peg A to peg B, is
trivial.
Comments:
The tower of Hanoi is frequently used in
psychological research on problem solving.
This problem is frequently used in
neuro-psychological diagnosis and treatment of executive functions.
The tower of Hanoi is also used as backup rotation
scheme when performing computer data backups where multiple tabs/media are
involved.
This problem is very popular for teaching recursive
algorithm to beginning programming students.
A pictorial version of this puzzle is programmed
into emacs editor, accessed by typing M - X Hanoi.
The tower of Hanoi is also used as a test by
neuro-psychologists trying to evaluate frontal lobe deficits.
Cryptarithmatic Problem
Definition:
ÔÇťIt is an arithmetic problem which is represented i n letters. It
involves the decoding of digit represented by a character. It is in the form of
some arithmetic equation where digits are distinctly represented by some
characters. The problem requires finding of the digit represented by each
character. Assign a decimal digit to each of the letters in such a way that the
answer to the problem is correct. If the same letter occurs more than once, it
must be assigned the same digit each time. No two different letters may be
assigned the same digitÔÇŁ.
Procedure:
Cryptarithmatic problem is an interesting constraint satisfaction
problem for which different algorithms have been developed. Cryptarithm is a
mathematical puzzle in which digits are replaced by letters of the alphabet or
other symbols. Cryptarithmatic is the science and art of creating and solving
cryptarithms.
The different constraints of defining a cryptarithmatic problem are as
follows.
1)
Each letter or symbol represented
only one and a unique digit throughout the problem.
2)
When the digits replace letters
or symbols, the resultant arithmetical operation must be correct. The above two
constraints lead to some other restrictions in the problem.
For example:
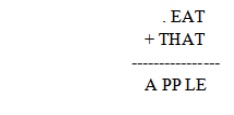
Consider that, the base of the number is 10. Then there must be at most
10 unique symbols or letters in the problem. Otherwise, it would not possible
to assign a unique digit to unique letter or symbol in the problem. To be
semantically meaningful, a number must not begin with a 0. So, the letters at
the beginning of each number should not correspond to 0. Also one can solve the
problem by a simple blind search. But a rule based searching technique can
provide the solution in minimum time.
Now, let us solve a simple cryptarithmatic puzzle given below.
Step 1:
In the above problem, M must be 1. You can visualize that, this is an
addition problem. The sum of two four digit numbers cannot be more than 10,000.
Also M cannot be zero according to the rules, since it is
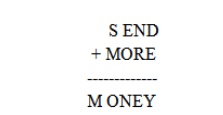
the first letter.
So now you have the problem like
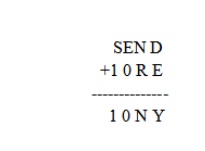
Step 2:
Now in the column s10, s+1 Ôëą 10. S must be 8 because there is a 1
carried over from the column EON or 9. O must be 0 (if s=8 and there is a 1
carried or s = 9 and there is no 1 carried) or 1 (if s=9 and there is a 1
carried). But 1 is already taken, so O must be 0.

Step 3:
There cannot be carry from column EON because any digit +0 < 10,
unless there is a carry from the column NRE, and E=9; But this cannot be the
case because then N would be 0 and 0 is already taken. So E < 9 and there is
no carry from this column. Therefore S=9 because 9+1=10.
Step 4:
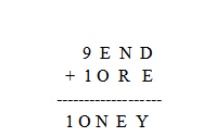
In the column EON, E cannot be equal to N. So there must be carry from
the column NRE; E+1=N. We now look at the column NRE, we know that E+1=N. Since
we know that carry from this column, N+R=1E (if there is no carry from the
column DEY) or N+R+1=1E (if there is a carry from the column DEY).

Step 5:
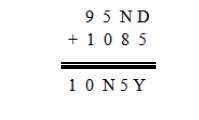

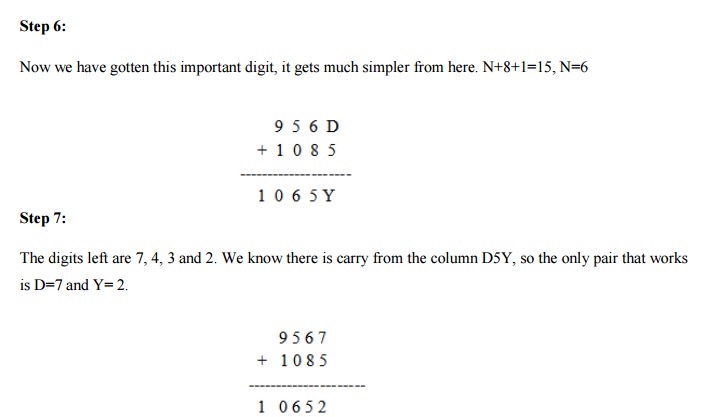
Which is final solution of the problem.
Comments:
This problem requires a lot of reasoning.
Time complexity of the problem is more as concerned
to the other problems.
This problem can also be solved by the evolutionary
approach and mutation operations.
This problem is dependent upon some constraints
which are necessary part of the problem. Various complex problems can also be
solved by this technique.
Related Topics