Chapter: Artificial Intelligence(AI) : Planning and Machine Learning
Statistical Reasoning
Statistical Reasoning :
.
In the logic based approaches
described, we have assumed that everything is either believed false or believed
true.
However, it is often useful to
represent the fact that we believe such that something is probably true, or
true with probability (say) 0.65.
This is useful for dealing with
problems where there is randomness and unpredictability (such as in games of chance) and also for dealing with problems where we could, if we had sufficient information, work out
exactly what is true.
To do all this in a principled way
requires techniques for probabilistic reasoning. In this section, the Bayesian Probability Theory is first described and then discussed how uncertainties are treated.
Recall glossary of terms
.
Ō¢Ā Probabilities :
Usually, are descriptions of the
likelihood of some event occurring (ranging from 0 to 1).
Ō¢Ā Event :
One or more outcomes of a probability
experiment .
Ō¢Ā Probability Experiment :
Process which leads to well-defined
results call outcomes.
Ō¢Ā Sample Space :
Set of all possible outcomes of a
probability experiment.
Ō¢Ā
Independent Events :
Two events, E1 and E2, are
independent if the fact that E1 occurs does not affect the probability of E2
occurring.
Ō¢Ā Mutually Exclusive Events :
Events E1, E2, ..., En are said to
be mutually exclusive if the occurrence of any one of them automatically
implies the non-occurrence of the remaining n ŌłÆ 1 events.
Ō¢Ā Disjoint Events :
Another name for mutually exclusive
events.
Ō¢Ā Classical Probability :
.
Also called a priori theory of
probability.
The probability of event A = no of possible outcomes f divided by the total no of possible outcomes n ; ie., P(A) = f / n.
Assumption: All possible outcomes
are equal likely.
Ō¢Ā Empirical Probability :
Determined analytically, using
knowledge about the nature of the experiment rather than through actual
experimentation.
Ō¢Ā Conditional Probability :
The probability of some event A, given the occurrence of some other event B. Conditional probability is written P(A|B), and read as "the probability
of A, given B ".
Ō¢Ā Joint probability :
The probability of two events in
conjunction. It is the probability of both events together. The joint
probability of A and B is written P(A Ōł®
; also
written as P(A, B).
Marginal Probability :
The probability of one event,
regardless of the other event. The marginal probability of A is written P(A), and the marginal probability of B is written P(B).
Examples
Ō¢Ā Example 1
Sample Space - Rolling two dice
The sums can be { 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 }.
Note that each of these are not
equally likely. The only way to get a sum 2 is to roll a 1 on both dice, but can get a sum 4 by rolling out comes as (1,3), (2,2), or (3,1).
Table below illustrates a sample
space for the sum obtain.
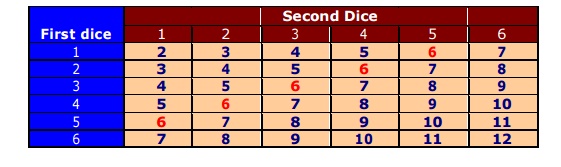
Classical Probability
Table below illustrates frequency
and distribution for the above sums.

The classical probability is the
relative frequency of each event.
Classical probability P(E) = n(E) / n(S); P(6) = 5 / 36, P(8) = 5 / 36
Empirical Probability
The empirical probability of an
event is the relative frequency of a frequency distribution based upon
observation P(E) = f / n
Ō¢Ā Example 2
Mutually Exclusive Events (disjoint) : means nothing in common
Two events are mutually exclusive
if they cannot occur at the same time.
If two events are mutually exclusive,
then probability of both occurring
at same time is P(A and B) = 0
If two events are mutually
exclusive ,
then the probability of either
occurring is P(A or B) = P(A) + P(B)
Given P(A)= 0.20, P(B)= 0.70, where
A and B are disjoint
then P(A and B) = 0
The table below indicates
intersections ie "and" of each pair of events. "Marginal"
means total; the values in bold means given; the rest of the values are
obtained by addition and subtraction.
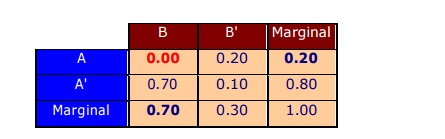
Non-Mutually Exclusive Events
The non-mutually exclusive events
have some overlap.
When P(A) and P(B) are added, the probability of the
intersection (ie. "and" ) is added twice, so subtract once.
P(A or B) = P(A) + P(B) - P(A and
B)
Given : P(A) = 0.20, P(B)
= 0.70, P(A and B) = 0.15
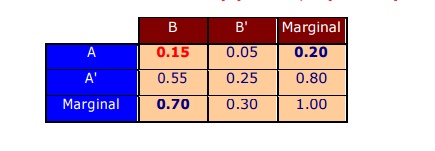
Ō¢Ā Example 3
Factorial , Permutations and
Combinations
Factorial
The factorial of an integer n Ōēź 0 is written as n! .
n! = n ├Ś n-1 ├Ś . . . ├Ś 2 ├Ś 1.
and in particular, 0! = 1.
It is, the number of permutations
of n distinct objects;
e.g., no of ways to arrange 5
letters A, B, C, D and E into a word is
5!
5! =
5 x 4 x 3 x 2 x 1 = 120
N! =
(N) x (N-1) x (N-2) x . . . x (1)
n! =
n (n - 1)! , 0! = 1
Permutation
The permutation is arranging
elements (objects or symbols) into distinguishable sequences. The ordering of
the elements is important. Each unique ordering is a permutation.
Number of permutations of ŌĆ× n ŌƤ different things taken ŌĆ× r ŌƤ at a time is given by
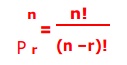
(for convenience in writing, here
after the symbol Pnr is written as nPr or P(n,r) )
Example 1
Consider a total of 10 elements, say integers {1, 2, ..., 10}. A permutation of 3 elements from this set is (5, 3, 4). Here n = 10 and r = 3.
The number of such unique sequences
are calculated as P(10,3) = 720.
Example 2
Find the number of ways to arrange
the three letters in the word
CAT in to two-letter groups like CA
or AC and no repeated letters.
This means permutations are of size
r = 2 taken from a set of size n = 3. so P(n, r) = P(3,2) = 6.
The ways are listed as CA CT AC AT
TC TA.
Similarly, permutations of size r =
4, taken from a set of size n = 10,
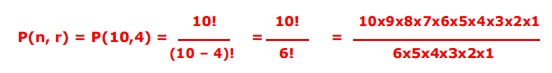
Combinations
Combination means selection of
elements (objects or symbols). The ordering of the elements has no importance.
Number of Combination of ŌĆ× n ŌƤ different things, taken ŌĆ× r ŌƤ at a time is

(for convenience in writing, here
after the symbol Cnr is written as nCr or C(n,r) )
Example
Find the number of combinations of
size 2 without repeated letters that can be made from the three letters
in the word CAT, order doesn't matter;
This means combinations of size r =2 taken from a set of size n = 3,

Related Topics