Fuzzy Logic

Fuzzy Logic

We have discussed only binary valued logic and classical set theory like :

A person belongs to a set of all human beings, and if given a specific subset, say all males, then one can say whether or not the particular person belongs to this set.

This is ok since it is the way human reason. e.g.,

IF person is male AND a parent THEN person is a father. The rules are formed using operators.

Here, it is intersection operator "AND" which manipulates the sets. However, not everything can be described using binary valued sets.

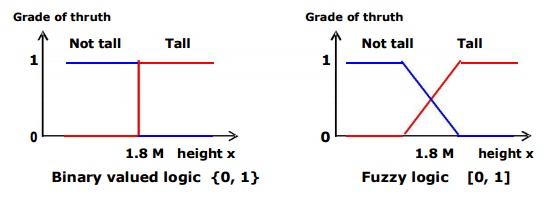
The grouping of persons into "male" or "female" is easy, but as "tall" or "not tall" is problematic.

A set of "tall" people is difficult to define, because there is no distinct cut-off point at which tall begins.

Fuzzy logic was suggested by Zadeh as a method for mimicking the ability of human reasoning using a small number of rules and still producing a smooth output via a process of interpolation.

Description of Fuzzy Logic

.

With fuzzy logic an element could partially belong to a set represented by the set membership. Example, a person of height 1.79 m would belong to both tall and not tall sets with a particular degree of membership.

Difference between binary logic and fuzzy logic

A fuzzy logic system is one that has at least one system component that uses fuzzy logic for its internal knowledge representation.

Fuzzy system communicate information using fuzzy sets.

Fuzzy logic is used purely for internal knowledge representation and externally it can be considered as any other system component.

Fuzzy Membership

Example : Five tumblers

Consider two sets: F and E.

F is set of all tumblers belong to the class full, and

E is set of all tumblers belong to the class empty

Definition of the set F and E

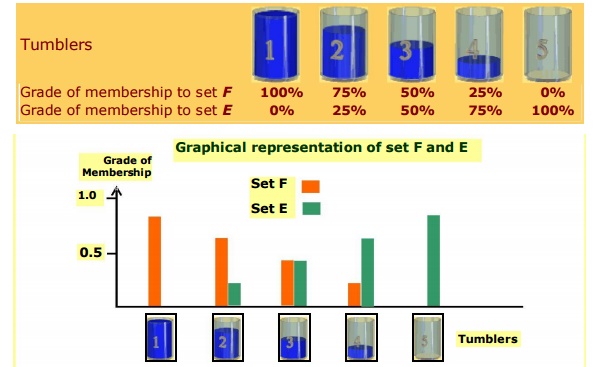
The sets F and E have some elements, having partial membership.

Such kind of non-crisp sets are called fuzzy sets.

The set "all tumblers" here is the basis of the fuzzy sets F and E, is called the base set.