Chapter: Artificial Intelligence(AI) : Planning and Machine Learning
Bayesian Networks and Certainty Factors
Bayesian Networks and Certainty Factors
.
A Bayesian network (or a belief network) is a probabilistic graphical model that represents a set of variables and their probabilistic independencies. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
Bayesian Networks are also called : Bayes nets, Bayesian Belief Networks (BBNs) or simply Belief Networks. Causal Probabilistic Networks (CPNs).
A Bayesian network consists of :
a set of nodes and a set of directed edges between nodes.
the edges reflect cause-effect relations within the domain.
The effects are not completely deterministic (e.g. disease -> symptom).
the strength of an effect is modeled as a probability.
Bayesian Networks
We have applied Bayesian probability theory, in earlier three examples (example 1, 2, and 3) , to relate two or more events. But this can be used to relate many events by tying them together in a network.
Consider the previous example 3 - Clinic trial
The trial says, the probability of the patients having HIV virus is 0.15.
A blood test done on patients :
If patient has virus, the test is +ve with probability 0.95.
If the patient does not have the virus, the test is +ve with probability 0.02.
This means given : P(H) = 0.15 ; P(P|H) = 0.95 ; P(P|¬H) = 0.02
Imagine, the patient is given a second test independently of the first; means the second test is done at a later date by a different person using different equipment. So, the error on the first test does not affect the probability of an error on the second test.
In other words the two tests are independent. This is depicted using the diagram below :
A simple example of a Bayesian Network.
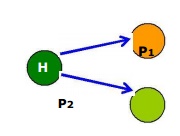
Event H is the cause of the two events P1 and P2.
The arrows represent the fact that H is driving P1 and P2.
The network contained 3 nodes.
If both P1 and P2 are +ve then find the probability that patient has the virus ? In
other words asked to find P(H|P1 Ōł® P2) .
How to find ?
Ō¢Ā Bayes Theorem

As worked before for P(P) which is the probability of a +ve result, here again break this into two separate cases:
patient has virus and both tests are +ve
patient not having virus and both tests are +ve
As before use the second axiom of probability
P(P1 Ōł® P2) = P(P1 Ōł® P2 |H) P(H) + P(P1 Ōł® P2 |┬¼H) P(┬¼H)
ŌĆĪ Because the two tests are independent given H we can write :
P(P1 Ōł® P2) = P(P1|H) P(P2|H) P(H) + P(P1|┬¼H) P(P2|┬¼H) P(┬¼H)
0.95 ├Ś 0.95 ├Ś 0.15 + 0.02├Ś 0.02 ├Ś 0.85
0.135715
Substitute this into Bayes Theorem above and obtain

Note : The results while two independent HIV tests performed Previously we calculated the probability, that the patient had HIV
given one +ve test, as 0.8934.
Later second HIV test was performed. After two +ve tests, we see that the probability has gone up to 0.99749.
So after two +ve tests it is more certain that the patient does have the HIV virus.
The next slide : a case where one tests is +ve and other is -ve.
Case where one tests is +ve and other is -ve.
This means, an error on one of the tests but we donŌƤt know which one; it may be any one.
P(H| P1 Ōł® ┬¼P2).
The issue is - whether the patient has HIV virus or not ?
ŌĆĪ We need to calculate
Following same steps for the case of two +ve tests, write Bayes Theorem

ŌĆĪ Note :
Belief in H, the event that the patient has virus, has increased.
Prior belief was 0.15 but it has now gone up to 0.299.
This appears strange because we have been given two contradictory pieces of data. But looking closely we see that probability of an error in each case is not equal.
The probability of a +ve test when patient is actually -ve is 0.02. The probability of a -ve test when patient is actually +ve is 0.05. Therefore we are more inclined to believe an error on the second test and this slightly increases our belief that the patient is +ve.
More Complicated Bayesian Networks
.
The previous network was simple contained three nodes. Let us look at a slightly more complicated one in the context of heart disease.
Given the following facts about heart disease.
Either smoking or bad diet or both can make heart disease more likely.
Heart disease can produce either or both of the following two symptoms:
high blood pressure
an abnormal electrocardiogram
Here smoking and bad diet are regarded as causes of heart disease. The heart disease in turn is a cause of high blood pressure and an abnormal electrocardiogram.
Ō¢Ā An appropriate network for heart disease is represented as
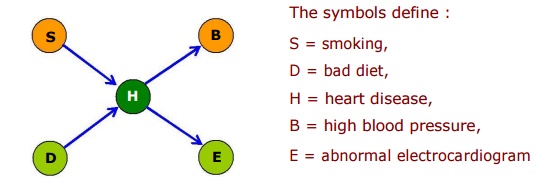
Here H has two causes S and D.
Find probability of H, given each of the four possible
combinations of
A medical survey gives us the following data :
P(S) = 0.3 P(D) = 0.4
P(H| S Ōł® D) = 0.8
P(H| ┬¼S Ōł® D) = 0.5
P(H| S Ōł® ┬¼D) = 0.4
P(H| ┬¼S Ōł® ┬¼D) = 0.1
P(B|H) = 0.7 P(B|¬H) = 0.1
P(E|H) = 0.8 P(E|¬H) = 0.1
Given these information, an answer to the question concerning this network :
what is the probability of heart disease ?
[Note : The interested students may try to the find answer.]
Related Topics