What is Artificial intelligence(AI)?

What is Artificial intelligence(AI)?

 

Artificial intelligence (AI) is the intelligence exhibited by machines or software. It is also the name of the academic field of study which studies how to create computers and computersoftware that are capable of intelligent behavior. The central problems (or goals) of AI research include reasoning, knowledge, planning, learning, natural language processing (communication), perception and the ability to move and manipulate objects.

 

Example

 

Cleverbot

 

Cleverbot is a chatterbot that’s modeled after human behavior and able to hold a conversation. It does so by remembering words from conversations. The responses are not programmed. Instead, it finds keywords or phrases that matches the input and searches through its saved conversations to find how it should respond to the input.

 

MySong

 

MySong is an application which can help people who has no experience in write a song or even can not play any instrument, to create original music by themselves. It will automatically choose chords to accompany the vocal melody that you have just inputed by microphone. In the other hand, MySong can help songwriters to record their new ideas and melodies no matter where and when they are. But MySong is not a professional application which can produce or edit your song, then it means you have to use other tools or software to really develop a song.

 

Artificial Intelligence in Video Games

 

The AI components used in video games is often a slimmed down version of a true AI implementation, as the scope of a video game is often limited (ie Console memory capacity). The most innovative use of AI is garnered on Personal Computers, whose memory capabilities are adjustable beyond the capacity of modern gaming consoles.

 

Some examples of AI components typically used in video games are Path Finding, Adaptiveness (learning), perception, and planning (decision making).

 

The present state of video games can offer a variety of "worlds" for AI concepts to be tested in, such as a static or dynamic environment, deterministic or non-deterministic transitioning, and fully or partially known game worlds. The real-time performance constraint of AI in video game processing must also be considered, which is another contributing factor to why video games may choose to implement a "simple" AI, ie: finite state machine as AI, which may not even be considered Artifical Intelligence at heart.

 

Artificial Intelligence in Mobile System

 

As smartphone come into our daily life, we need to the make our device even more clever. Recently, researchers are trying to apply traditional AI techniques into mobile environment. Those techniques, including speech recognition, machine learning, classification and natural language processing give us a more powerful application, such as SIRI on iOS, kinect from Microsoft. AI on mobile device introduces some new challenges, such as limited computation resource and energy consumption etc.

 

History of AI

 

Cybernetics and early neural networks Turing's test

 

Game AI

 

Symbolic reasoning and the Logic Theorist AI

 

 

Problem Formulation

 

States possible world states accessibility the agent can determine via its sensors in which state it is consequences of actions the agent knows the results of its actions levels problems and actions can be specified at various levels constraints conditions that influence the problem-solving process Performance measures to be applied costs utilization of resources

 

Problem Types

 

single-state problem

multiple-state problem

 

 

contingency problem exploration problem

 

Single-State Problem

 

Exact prediction is possible state is known exactly after any sequence of actions accessibility of the world all essential information can be obtained through sensors consequences of actions are known to the agent goal

 

for each known initial state, there is a unique goal state that is guaranteed to be reachable via an action sequence simplest case, but severely restricted

 

Multiple-State Problem

 

Semi-exact prediction is possible state is not known exactly, but limited to a set of possible states after each action accessibility of the world not all essential information can be obtained through sensors reasoning can be used to determine the set of possible states consequences of actions are not always or completely known to the agent; actions or the environment might exhibit randomness goal due to ignorance, there may be no fixed action sequence that leads to the goal less restricted, but more complex.

 

Contingency Problem

 

Exact prediction is impossible state unknown in advance, may depend on the outcome of actions and changes in the environment accessibility of the world some essential information may be obtained through sensors only at execution time consequences of actions may not be known at planning time goal instead of single action sequences, there are trees of actions contingency branching point in the tree of actions agent design different from the previous two cases: the agent must act on incomplete plans

 

Exploration Problem

 

Effects of actions are unknown state the set of possible states may be unknown accessibility of the world some essential information may be obtained through sensors only at execution time consequences of actions may not be known at planning time goal can’t be completely formulated in advance because states and consequences may not be known at planning time discovery what states exist experimentation what are the outcomes of actions learning remember and evaluate experiments

MATCHING

 

Clever search involves choosing from among the rules that can be applied at a particular point, the ones that are most likely to lead to a solution. We need to extract from the entire collection of rules, those that can be applied at a given point. To do so requires some kind of matching between the current state and the preconditions of the rules.

 

How should this be done?

 

One way to select applicable rules is to do a simple search through all the rules comparing one’s preconditions to the current state and extracting all the ones that match . this requires indexing of all the rules. But there are two problems with these simple solutions:

 

It requires the use of a large number of rules. Scanning through all of them would be hopelessly inefficeint.

 

It is not always immediately obvious whether a rule’s preconditions are satisfied by a particular state.

 

Sometimes , instead of searching through the rules, we can use the current state as an index into the rules and select the matching ones immediately. In spite of limitations, indexing in some form is very important in the efficient operation of rules based systems.

 

A more complex matching is required when the preconditions of rule specify required properties that are not stated explicitly in the description of the current state. In this case, a separate set of rules must be used to describe how some properties can be inferred from others. An even more complex matching process is required if rules should be applied and if their pre condition approximately match the current situation. This is often the case in situations involving physical descriptions of the world.

 

LEARNING

 

Learning is the improvement of performance with experience over time.

 

Learning element is the portion of a learning AI system that decides how to modify the performance element and implements those modifications.

 

We all learn new knowledge through different methods, depending on the type of material to be learned, the amount of relevant knowledge we already possess, and the environment in which the learning takes place. There are five methods of learning . They are,

 

Memorization (rote learning)

 

Direct instruction (by being told)

 

Analogy

 

Induction

 

Deduction

 

Learning by memorizations is the simplest from of le4arning. It requires the least amount of inference and is accomplished by simply copying the knowledge in the same form that it will be used directly into the knowledge base.

Example:- Memorizing multiplication tables, formulate , etc.

 

Direct instruction is a complex form of learning. This type of learning requires more inference than role learning since the knowledge must be transformed into an operational form before learning when a teacher presents a number of facts directly to us in a well organized manner.

 

Analogical learning is the process of learning a new concept or solution through the use of similar known concepts or solutions. We use this type of learning when solving problems on an exam where previously learned examples serve as a guide or when make frequent use of analogical learning. This form of learning requires still more inferring than either of the previous forms. Since difficult transformations must be made between the known and unknown situations.

 

Learning by induction is also one that is used frequently by humans . it is a powerful form of learning like analogical learning which also require s more inferring than the first two methods. This learning re quires the use of inductive inference, a form of invalid but useful inference. We use inductive learning of instances of examples of the concept. For example we learn the

 

concepts of color or sweet taste after experiencing the sensations associated with several examples of colored objects or sweet foods.

 

Deductive learning is accomplished through a sequence of deductive inference steps using known facts. From the known facts, new facts or relationships are logically derived. Deductive learning usually requires more inference than the other methods.

 

Review Questions:-

 

what is perception ?

 

How do we overcome the Perceptual Problems?

 

Explain in detail the constraint satisfaction waltz algorithm?

 

What is learning ?

 

What is Learning element ?

 

List and explain the methods of learning?

 

Types of learning:- Classification or taxonomy of learning types serves as a guide in studying or comparing a differences among them. One can develop learning taxonomies based on the type of knowledge representation used (predicate calculus , rules, frames), the type of knowledge learned (concepts, game playing, problem solving), or by the area of application(medical diagnosis , scheduling , prediction and so on).

 

The classification is intuitively more appealing and is one which has become popular among machine learning researchers . it is independent of the knowledge domain and the representation scheme is used. It is based on the type of inference strategy employed or the methods used in the learning process. The five different learning methods under this taxonomy are:

 

Memorization (rote learning)

Direct instruction(by being told)

 

Analogy

 

Induction

 

Deduction

 

Learning by memorization is the simplest form of learning. It requires the least5 amount of inference and is accomplished by simply copying the knowledge in the same form that it will be used directly into the knowledge base. We use this type of learning when we memorize multiplication tables ,

 

for example.

 

A slightly more complex form of learning is by direct instruction. This type of learning requires more understanding and inference than role learning since the knowledge must be transformed into an operational form before being integrated into the knowledge base. We use this type of learning when a teacher presents a number of facts directly to us in a well organized manner.

 

The third type listed, analogical learning, is the process of learning an ew concept or solution through the use of similar known concepts or solutions. We use this type of learning when solving problems on an examination where previously learned examples serve as a guide or when we learn to drive a truck using our knowledge of car driving. We make frewuence use of analogical learning. This form of learning requires still more inferring than either of the previous forms, since difficult transformations must be made between the known and unknown situations. This is a kind of application of knowledge in a new situation.

 

The fourth type of learning is also one that is used frequency by humans. It is a powerful form of learning which, like analogical learning, also requires more inferring than the first two methods. This form of learning requires the use of inductive inference, a form of invalid but useful inference. We use inductive learning when wed formulate a general concept after seeing a number of instance or examples of the concept. For example, we learn the concepts of color sweet taste after experiencing the sensation associated with several examples of colored objects or sweet foods.

 

The final type of acquisition is deductive learning. It is accomplished through a sequence of deductive inference steps using known facts. From the known facts, new facts or relationships are logically derived. Deductive learning usually requires more inference than the other methods. The inference method used is, of course , a deductive type, which is a valid from of inference.

 

In addition to the above classification, we will sometimes refer to learning methods as wither methods or knowledge-rich methods. Weak methods are general purpose methods in which little or no initial knowledge is available. These methods are more mechanical than the classical AI knowledge

 

rich methods. They often rely on a form of heuristics search in the learning process.

 

 

Heuristic Search

 

All of the search methods in the preceding section are uninformed in that they did not take into account the goal. They do not use any information about where they are trying to get to unless they happen to stumble on a goal. One form of heuristic information about which nodes seem the most promising is a heuristic function h(n), which takes a node n and returns a non-negative real number that is an estimate of the path cost from node n to a goal node. The function h(n) is an underestimate if h(n) is less than or equal to the actual cost of a lowest-cost path from node n to a goal.

 

The heuristic function is a way to inform the search about the direction to a goal. It provides an informed way to guess which neighbor of a node will lead to a goal.

 

There is nothing magical about a heuristic function. It must use only information that can be readily obtained about a node. Typically a trade-off exists between the amount of work it takes to derive a heuristic value for a node and how accurately the heuristic value of a node measures the actual path cost from the node to a goal.

 

A standard way to derive a heuristic function is to solve a simpler problem and to use the actual cost in the simplified problem as the heuristic function of the original problem.

 

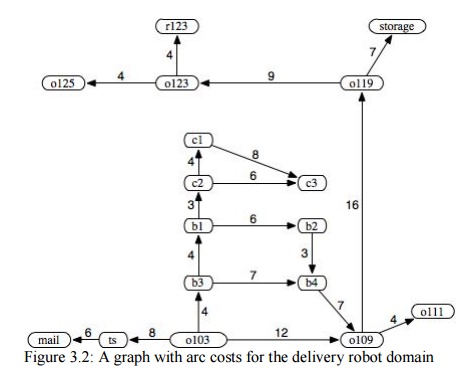
The straight-line distance in the world between the node and the goal position can be used as the heuristic function. The examples that follow assume the following heuristic function: h(mail) = 26 h(ts) = 23 h(o103) = 21

h(o109)       = 24  h(o111)       = 27 h(o119)        = 11

h(o123)       = 4    h(o125)       = 6    h(r123)       = 0

h(b1) = 13  h(b2) = 15  h(b3) = 17

h(b4) = 18  h(c1)  = 6    h(c2) = 10

h(c3)  = 12 h(storage)     = 12           

This h function is an underestimate because the h value is less than or equal to the exact cost of a lowest-cost path from the node to a goal. It is the exact cost for node o123. It is very much an underestimate for node b1, which seems to be close, but there is only a long route to the goal. It is very misleading for c1, which also seems close to the goal, but no path exists from that node to the goal.

 

where the state space includes the parcels to be delivered. Suppose the cost function is the total distance traveled by the robot to deliver all of the parcels. One possible heuristic function is the largest distance of a parcel from its destination. If the robot could only carry one parcel, a possible heuristic function is the sum of the distances that the parcels must be carried. If the robot could carry multiple parcels at once, this may not be an underestimate of the actual cost.

 

The h function can be extended to be applicable to (non-empty) paths. The heuristic value of a path is the heuristic value of the node at the end of the path. That is:

 

h( n_o,...,n_k )=h(n_k)

 

 

A simple use of a heuristic function is to order the neighbors that are added to the stack representing the frontier in depth-first search. The neighbors can be added to the frontier so that the best neighbor is selected first. This is known as heuristic depth-first search. This search chooses the locally best path, but it explores all paths from the selected path before it selects another path. Although it is often used, it suffers from the problems of depth-fist search.

 

Another way to use a heuristic function is to always select a path on the frontier with the lowest heuristic value. This is called best-first search. It usually does not work very well; it can follow paths that look promising because they are close to the goal, but the costs of the paths may keep increasing.

 

 

 

 

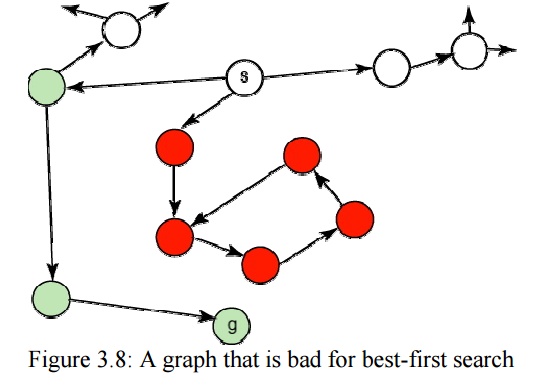
PROBLEM CHARACTERISTICS

 

Heuristic search is a very general method applicable to a large class of problem . It includes a variety of techniques. In order to choose an appropriate method, it is necessary to analyze the problem with respect to the following considerations.

 

Is the problem decomposable ?

 

A very large and composite problem can be easily solved if it can be broken into smaller problems and recursion could be used. Suppose we want to solve.

 

Ex:- ∫ x2 + 3x+sin2x cos 2x dx

 

This can be done by breaking it into three smaller problems and solving each by applying specific rules. Adding the results the complete solution is obtained.

 

2. Can solution steps be ignored or undone?

 

Problem fall under three classes ignorable , recoverable and irrecoverable. This classification is with reference to the steps of the solution to a problem. Consider thermo proving. We may later find that it is of no help. We can still proceed further, since nothing is lost by this redundant step. This is an example of ignorable solutions steps.

 

Now consider the 8 puzzle problem tray and arranged in specified order. While moving from the start state towards goal state, we may make some stupid move and consider theorem proving. We may proceed by first proving lemma. But we may backtrack and undo the unwanted move. This only involves additional steps and the solution steps are recoverable.

 

Lastly consider the game of chess. If a wrong move is made, it can neither be ignored nor be recovered. The thing to do is to make the best use of current situation and proceed. This is an example of an irrecoverable solution steps.

 

Ignorable problems Ex:- theorem proving

 

In which solution steps can be ignored.

 

Recoverable problems Ex:- 8 puzzle

 

In which solution steps can be undone

 

Irrecoverable problems Ex:- Chess

 

In which solution steps can’t be undone

 

A knowledge of these will help in determining the control structure.

 

3.. Is the Universal Predictable?

 

Problems can be classified into those with certain outcome (eight puzzle and water jug problems) and those with uncertain outcome ( playing cards) . in certain – outcome problems, planning could be done to generate a sequence of operators that guarantees to a lead to a solution. Planning helps to avoid unwanted solution steps. For uncertain out come problems, planning can at best generate a sequence of operators that has a good probability of leading to a solution. The uncertain outcome problems do not guarantee a solution and it is often very expensive since the number of solution and it is often very expensive since the number of solution paths to be explored increases exponentially with the number of points at which the outcome can not be predicted. Thus one of the hardest types of problems to solve is the irrecoverable, uncertain – outcome problems ( Ex:-Playing cards).

 

4. Is good solution absolute or relative ?

 

(Is the solution a state or a path ?)

 

There are two categories of problems. In one, like the water jug and 8 puzzle problems, we are satisfied with the solution, unmindful of the solution path taken, whereas in the other category not just any solution is acceptable. We want the best, like that of traveling sales man problem, where it is the shortest path. In any – path problems, by heuristic methods we obtain a solution and we do not explore alternatives. For the best-path problems all possible paths are explored using an exhaustive search until the best path is obtained.

 

5. The knowledge base consistent ?

 

In some problems the knowledge base is consistent and in some it is not. For example consider the case when a Boolean expression is evaluated. The knowledge base now contains theorems and laws of Boolean Algebra which are always true. On the contrary consider a knowledge base that contains facts about production and cost. These keep varying with time. Hence many reasoning schemes that work well in consistent domains are not appropriate in inconsistent domains.

 

Ex.Boolean expression evaluation.

 

6. What is the role of Knowledge?

 

Though one could have unlimited computing power, the size of the knowledge base available for solving the problem does matter in arriving at a good solution. Take for example the game of playing chess, just the rues for determining legal moves and some simple control mechanism is sufficient to arrive at a solution. But additional knowledge about good strategy and tactics could help to constrain the search and speed up the execution of the program. The solution would then be realistic.

 

Consider the case of predicting the political trend. This would require an enormous amount of knowledge even to be able to recognize a solution , leave alone the best.

 

Ex:- 1. Playing chess 2. News paper understanding

 

7. Does the task requires interaction with the person.

 

The problems can again be categorized under two heads.

 

Solitary in which the computer will be given a problem description and will produce an answer, with no intermediate communication and with he demand for an explanation of the reasoning process. Simple theorem proving falls under this category . given the basic rules and laws, the theorem could be proved, if one exists.

 

Ex:- theorem proving (give basic rules & laws to computer)

 

Conversational, in which there will be intermediate communication between a person and the computer, wither to provide additional assistance to the computer or to provide additional informed information to the user, or both problems such as medical diagnosis fall under this category, where people will be unwilling to accept the verdict of the program, if they can not follow its reasoning.

 

Ex:- Problems such as medical diagnosis.

 

8. Problem Classification

 

Actual problems are examined from the point of view , the task here is examine an input and decide which of a set of known classes.

 

Ex:- Problems such as medical diagnosis , engineering design.

FORMALIZING GRAPH SEARCHING

 

A directed graph consists of

 

a set N of nodes and

 

a set A of ordered pairs of nodes called arcs.

 

In this definition, a node can be anything. All this definition does is constrain arcs to be ordered pairs of nodes. There can be infinitely many nodes and arcs. We do not assume that the graph is represented explicitly; we require only a procedure that can generate nodes and arcs as needed.

 

The arc n₁,n₂  is an outgoing arc from n₁ and an incoming arc to n₂.

 

 

A node n₂ is a neighbor of n₁ if there is an arc from n₁ to n₂; that is, if n₁,n₂ ∈A. Note that being a neighbor does not imply symmetry; just because n₂ is a neighbor of n₁ does not mean that n₁ is necessarily a neighbor of n₂. Arcs may be labeled, for example, with the action that will take the agent from one state to another.

 

A path from node s to node g is a sequence of nodes n₀, n₁,..., n_k such that s=n₀, g=n_k, and n_i-1,n_i ∈A; that is, there is an arc from n_i-1 to n_i for each i. Sometimes it is useful to view a path as the sequence of arcs, n_o,n ₁ , n₁,n₂ ,..., n _k-1,n_k , or a sequence of labels of these arcs.

 

A cycle is a nonempty path such that the end node is the same as the start node - that is, a cycle is a path n₀, n ₁,..., n_k such that n₀=n_k and k≠0. A directed graph without any cycles is called a directed acyclic graph (DAG). This should probably be an acyclic directed graph, because it is a directed graph that happens to be acyclic, not an acyclic graph that happens to be directed, but DAG sounds better than ADG!

 

A tree is a DAG where there is one node with no incoming arcs and every other node has exactly one incoming arc. The node with no incoming arcs is called the root of the tree and nodes with no outgoing arcs are called leaves.

 

To encode problems as graphs, one set of nodes is referred to as the start nodes and another set is called the goal nodes. A solution is a path from a start node to a goal node.

 

Sometimes there is a cost - a positive number - associated with arcs. We write the cost of arc n_i,n_j as cost( n_i,n_j ). The costs of arcs induces a cost of paths.

 

 

Given a path p = n₀, n₁,..., n_k , the cost of path p is the sum of the costs of the arcs in the path:

 

cost(p) = cost( n₀,n₁ ) + ...+ cost( n_k-1,n_k )

 

An optimal solution is one of the least-cost solutions; that is, it is a path p from a start node to a goal node such that there is no path p' from a start node to a goal node where cost(p')<cost(p).