KR Using Predicate Logic

KR Using Predicate Logic

In the previous section much has been illustrated about knowledge and KR related issues. This section, illustrates :

How knowledge can be represented  as “symbol structures”  that  characterize bits of knowledge about objects, concepts, facts, rules, strategies;

Assumptions about KR :

Intelligent Behavior can be achieved by manipulation of symbol structures.

KR languages are designed to facilitate operations over symbol structures, have precise syntax and semantics;

Syntax  tells which expression is legal ?,

e.g., red1(car1), red1 car1, car1(red1), red1(car1 & car2) ?;  and

Semantic tells what an expression means ?

e.g., property “dark red” applies to my car.

Make Inferences, draw new conclusions from existing facts.

To satisfy these assumptions about KR, we need formal notation that allow automated inference and problem solving. One popular choice is use of logic.

Logic

Logic is concerned with the truth of statements about the world.

Generally each statement is either TRUE or FALSE.

Logic includes :  Syntax , Semantics and Inference Procedure.

Syntax :

Specifies the symbols in the language about how they can be combined to form sentences. The facts about the world are represented as sentences in logic.

Semantic :

Specifies how to assign a truth value to a sentence based on its meaning in the world. It Specifies what facts a sentence refers to.

A fact is a claim about the world, and it may be TRUE or FALSE.

Inference Procedure :

Specifies methods for computing new sentences from the existing sentences.

Note

Facts : are claims about the world that are True or False. Representation : is an expression (sentence), stands for the objects and relations.

Sentences : can be encoded in a computer program.

Logic as a KR Language

Logic is a language for reasoning, a collection of rules used while doing logical reasoning. Logic is studied as KR languages in artificial intelligence.

◊ Logic is a formal system in which the formulas or sentences have true or false values.

Problem of designing KR language is a tradeoff between that which is

Expressive enough to represent important objects and relations in a problem domain.

Efficient enough in reasoning and answering questions about implicit information in a reasonable amount of time.

Logics  are  of  different  types  :  Propositional  logic,  Predicate  logic,

Temporal logic, Modal logic, Description logic etc;

They represent things and allow more or less efficient inference.

Propositional logic and Predicate logic are fundamental to all logic.

Propositional Logic is the study of statements and their connectivity. Predicate Logic is the study of individuals and their properties.

1. Logic Representation

Logic can be used to represent simple facts.

The facts are claims         about the world that are True or False.

To build a Logic-based      representation :

User defines a set of primitive symbols and the associated semantics.

Logic defines ways of putting symbols together so that user can define legal sentences in the language that represent TRUE facts.

Logic defines ways of inferring new sentences from existing ones.

Sentences - either TRUE or false but not both are called propositions.

A declarative sentence expresses a statement with a proposition as content; example:

the declarative "snow is white" expresses that snow is white; further, "snow is white" expresses that snow is white is TRUE.

In this section, first Propositional Logic (PL) is briefly explained and then the Predicate logic is illustrated in detail.

Propositional Logic (PL)

A proposition is a statement, which in English would be a declarative sentence. Every proposition is either TRUE or FALSE.

Examples:  (a) The sky is blue.,   (b) Snow is cold. , (c) 12 * 12=144

Propositions are “sentences” ,  either true or false but not both.

A sentence is smallest unit in propositional logic.

‡ If proposition is true,  then truth value is "true" .

If proposition is false,    then truth value is "false" .

Propositional logic is  fundamental to all logic.

Propositional logic is also called Propositional calculus, Sentential calculus, or Boolean algebra.

Propositional logic tells the ways of joining and/or modifying entire propositions, statements or sentences to form more complicated propositions, statements or sentences, as well as the logical relationships and properties that are derived from the methods of combining or altering statements.

Statement, Variables and Symbols

These and few more related terms, such as, connective, truth value, contingencies, tautologies, contradictions, antecedent, consequent, argument are explained below.

◊ Statement

Simple statements (sentences), TRUE or FALSE, that does not contain any other statement as a part, are basic propositions; lower-case letters, p, q, r, are symbols for simple statements.

Large, compound or complex statement are constructed from basic propositions by combining them with connectives.

◊ Connective or Operator

The connectives join simple statements into compounds, and joins compounds into larger compounds.

Table below indicates, the basic connectives and their symbols :

listed in decreasing order of operation priority;

operations with higher priority is solved first.

Example of a formula : ((((a Λ ¬b) V c →  d) ↔  ¬ (a V c ))

Connectives and Symbols in decreasing order of operation priority

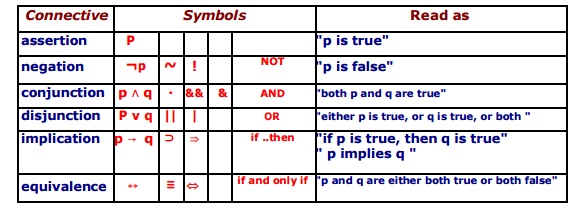
Note : The propositions and connectives are the basic elements of propositional logic.

◊ Truth Value

The truth value of a statement is its  TRUTH or FALSITY ,

Example : p

~p is either TRUE or FALSE, p v q is either TRUE or FALSE,

use " T " or

is either TRUE or FALSE, and so on.

1 " to mean TRUE. use " F " or

0 " to mean FALSE

Truth table defining the basic connectives :

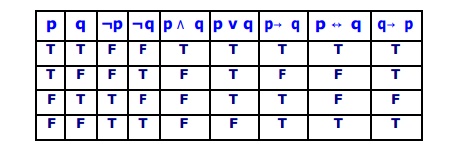
Tautologies

A proposition that is always true is called a "tautology".

e.g., (P v ¬P) is always true regardless of the truth value of the proposition P.

Contradictions

A proposition that is always false is called a "contradiction".

e.g., (P ∧ ¬P) is always false regardless of the truth value of the proposition P.

◊ Contingencies 

A proposition  is called a "contingency" , if that proposition is neither a tautology nor a contradiction .

e.g., (P v Q)    is a contingency.

Antecedent, Consequent

These two are parts of conditional statements. In the conditional statements, p → q , the

1st statement or "if - clause" (here p) is called antecedent ,

2nd statement or "then - clause" (here q) is called consequent.

Argument

An argument is a demonstration or a proof of some statement. Example : "That bird is a crow; therefore, it's black."

Any argument can be expressed as a compound statement.

In logic, an argument is a set of one or more meaningful declarative sentences (or "propositions") known as the premises along with another meaningful declarative sentence (or

"proposition") known as the conclusion.

Premise is a proposition which gives reasons, grounds, or evidence for accepting some other proposition, called the conclusion. Conclusion is a proposition, which is purported to be established on the basis of other propositions.

Take all the premises, conjoin them, and make that conjunction the antecedent of a conditional and make the conclusion the consequent. This implication statement is called the corresponding conditional of the argument.

Note : Every argument has a corresponding conditional, and every implication statement has a corresponding argument. Because the corresponding conditional of an argument is a statement, it is therefore either a tautology, or a contradiction, or a contingency.

An argument is valid

"if and only if" its corresponding conditional is a tautology.

Two statements are consistent

"if and only if" their conjunction is not a contradiction.

Two statements are logically equivalent

"if and only if" their truth table columns are identical;

"if and only if" the statement of their equivalence using " ≡ " is a tautology.

Note : The truth tables are adequate to test validity, tautology, contradiction, contingency, consistency, and equivalence.

Predicate Logic

The propositional logic, is not powerful enough for all types of assertions;

Example : The assertion "x > 1", where x is a variable, is not a proposition because it is neither true nor false unless value of x is defined.

For x > 1 to be a proposition ,

either we substitute a specific number for x ;

or change it to something like

"There is a number x for which x > 1 holds";

or "For every number x, x > 1 holds".

Consider example :

“ All men are mortal.

Socrates is a man.

Then Socrates is mortal” ,

These cannot be expressed in propositional logic as a finite and logically valid argument (formula).

We need languages : that allow us to describe properties ( predicates ) of objects, or a relationship among objects represented by the variables .

Predicate logic satisfies the requirements of a language.

Predicate logic is powerful enough for expression and reasoning.

Predicate logic is built upon the ideas of propositional logic.

Predicate :

Every complete "sentence" contains two parts : a "subject" and a "predicate".

The subject is what (or whom) the sentence is about. The predicate tells something about the subject;

Example :

A  sentence     "Judy {runs}".

The subject     is Judy  and    the predicate is runs .

Predicate, always includes verb, tells something about the subject.

Predicate is a verb phrase template that describes a property of objects, or a relation among objects represented by the variables. Example:

“The car Tom is driving is blue" ; "The sky is blue" ;

"The cover of this book is blue"

Predicate                 is “is blue" ,       describes property.

Predicates are given names; Let „B‟ is name for predicate "is_blue". Sentence is represented as "B(x)" , read as "x is blue";

Symbol     “x” represents          an arbitrary Object .

Predicate Logic Expressions :

The propositional operators combine predicates, like

If ( p(....) && ( !q(....) || r (....) ) )

Logic operators :

Examples of  disjunction (OR) and conjunction (AND).

Consider the expression with the respective logic symbols || and &&

x < y || ( y < z && z < x)    

which is   true || ( true &&    true)       ;

Applying truth table, found    True       

Assignment for < are   3, 2, 1 for  x, y, z     and then

the value can be FALSE or TRUE          

3 < 2 || ( 2 < 1 && 1 < 3)   

It is False             

Predicate Logic Quantifiers

As said before,x > 1 is not proposition and why ?

Also said, that for  x > 1 to be a proposition what is required ?

Generally, a predicate with variables (is called atomic formula) that can be made a proposition by applying one of the following two operations to each of its variables :

Assign a value to the variable; e.g., x > 1, if 3 is assigned to x becomes 3 > 1 , and it then becomes a true statement, hence a proposition.

Quantify the variable using a quantifier on formulas of predicate logic (called wff well-formed formula), such as x > 1 or P(x), by using Quantifiers on variables.

Apply Quantifiers on Variables

Variable  x

x > 5 is not a proposition, its truth depends upon the value of variable x

to reason such statements, x need to be declared

Declaration x : a

x : a  declares variable x

x : aread as  “x is an element of set a”

Statement   p is a statement about x

Q x : a • pis quantification of statement

Universe of Discourse

The universe of discourse, also called domain of discourse or universe.

This indicates :

a set of entities that the quantifiers deal.

entities can be set of real numbers, set of integers, set of all cars on a parking lot, the set of all students in a classroom etc.

universe is thus the domain of the (individual) variables.

propositions in the predicate logic are statements on objects of a universe.

The universe is often left implicit in practice, but it should be obvious from the context.

Examples:

About "natural numbers" forAll x, y (x < y or x = y or x > y), there is no need to be more precise and say forAll x, y in N, because N is implicit, being the universe of discourse.

About a property that holds for natural numbers but not for real numbers, it is necessary to qualify what the allowable values of x and y are.

■  Apply Existential Quantifier

Existential Quantification allows us to state that an object does exist without naming it.

Formula

In mathematical logic, a formula is a type of abstract object.

A token of a formula is a symbol or string of symbols which may be interpreted as any meaningful unit in a formal language.

‡ Terms

Defined recursively as variables, or constants, or functions like f(t1, . . . , tn), where f is an n-ary function symbol, and t1, . . . , tn are terms. Applying predicates to terms produces atomic formulas.

‡  Atomic formulas

An atomic formula (or simply atom) is a formula with no deeper propositional structure, i.e., a formula that contains no logical connectives or a formula that has no strict sub-formulas.

Atoms are thus the simplest well-formed formulas of the logic.

Compound formulas are formed by combining the atomic formulas using the logical connectives.

Well-formed formula ("wiff") is a symbol or string of symbols (a formula) generated by the formal grammar of a formal language.

An atomic formula is one of the form :

2. Representing “ IsA ” and “ Instance ” Relationships

Logic  statements,            containing  subject,  predicate,  and  object,  were

explained. Also stated, two important attributes "instance" and "isa", in a

hiera                  hical structure (Ref. Fig. Inheritable KR).

Attributes “ IsA ” and “ Instance ” support property inheritance and play important role in knowledge representation.

The ways these two attributes "instance" and "isa", are logically expressed are shown in the example below :

Example : A simple sentence like "Joe is a musician"

Here "is a" (called IsA) is a way of expressing what logically is called a class-instance relationship between the subjects represented by the terms "Joe" and "musician".

"Joe" is an instance of the class of things called "musician". "Joe" plays the role of instance,

"musician" plays the role of class in that sentence.

Note :  In such a sentence, while for a human there is no confusion,

but for computers each relationship have to be defined explicitly.

This is specified as: [Joe]       IsA  [Musician]

i.e.,  [Instance]      IsA  [Class]

3. Computable Functions and Predicates

The objective is to define class of functions C computable in terms of F.

This is expressed as C { F } is explained below using two examples :

"evaluate factorial n" and (2) "expression for triangular functions". ■ Example 1 : A conditional expression to define factorial n ie n!

◊ Expression

values T or F for true and false respectively.

◊ The value of ( p₁ → e_1, p₂ → e_2, . . . . . .p_n → e_n ) is the value of the e corresponding to the first p that has value T.

◊ The expressions defining n! , n= 5, recursively are : n! = n x (n-1)! for n ≥ 1

5! = 1 x 2 x 3 x 4 x 5 = 120 0! = 1

The above definition incorporates an instance that : if the product of no numbers ie 0! = 1 ,

then only, recursive relation (n + 1)! = (n+1) x n! works for n = 0 ◊ Use of the above conditional expressions to define functions n!

recursively is  n! = ( n = 0 →  1, n ≠ 0 →      n . (n – 1 ) ! )

◊ Example: Evaluate  2!

2! = ( 2 = 0 → 1, 2 ≠ 0 → 2 . ( 2 – 1 )! ) = 2 x 1!

= 2 x ( 1 = 0 → 1, 1 ≠ 0 → 1 . ( 1 – 1 )! ) = 2 x 1 x 0!

= 2 x 1 x ( 0 = 0 →  1, 0 ≠ 0 →                   0 . ( 0 – 1 )! )

= 2 x 1 x 1

=2

■  Example 2 : A conditional expression for triangular functions

◊ The graph of a well known triangular function is shown below

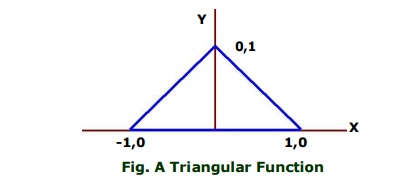
the conditional expressions for triangular functions are

= (x < 0 →   -x ,  x ≥ 0 →  x)

the triangular function of the above graph is represented by the conditional expression

tri (x) = (x ≤ -1 → 0, x ≤  0 →  -x, x ≤  1 →  x, x >1 →  0)

4. Resolution

Resolution is a procedure used in proving that arguments which are expressible in predicate logic are correct.

Resolution is a procedure that produces proofs by refutation or contradiction.

Resolution lead to refute a theorem-proving technique for sentences in propositional logic and first-order logic.

Resolution is a rule of inference.

Resolution is a computerized theorem prover.

Resolution is so far only defined for Propositional Logic. The strategy is that the Resolution techniques of Propositional logic be adopted in Predicate Logic.