KR Using Rules

KR Using Rules

In the earlier slides, theKnowledge    representations  using    predicate  logic have      been          illustrated.  The    other  popular  approaches  to  Knowledge representation are called production rules , semantic net and  frames.

Production rules, sometimes called IF-THEN rules are most popular KR.

production rules are simple but powerful forms of KR.

production rules provide the flexibility of combining declarative and procedural representation for using them in a unified

form. Examples of production rules :

IF condition THEN action

IF premise  THEN conclusion

IF proposition p1 and proposition p2 are true THEN proposition p3 is true

Advantages of production rules :

they are modular,

each rule define a small and independent piece of knowledge. − new rules may be added and old ones deleted

rules are usually independently of other rules.

The production rules as knowledge representation mechanism are used in the design of many "Rule-based systems" also called "Production systems" .

Types of Rules

Three types of rules are mostly used in the Rule-based production systems.

■ Knowledge Declarative Rules :

These rules state all the facts and relationships about a problem. Example :

IF inflation                    rate  declines

THEN  the                    price  of gold goes down.

These rules are a part of the knowledge base.

■                Inference Procedural Rules

These rules advise on how to solve a problem, while certain facts are known.

Example :

IF the data needed is not in the system THEN request it from the user.

These rules are part of the inference engine.

Meta rules

These are rules for making rules. Meta-rules reason about which rules should be considered for firing.

Example :

IF the rules which do not mention the current goal in their premise, AND there are rules which do mention the current goal in their premise, THEN the former rule should be used in preference to the latter.

Meta-rules direct reasoning rather than actually performing reasoning.

Meta-rules specify which rules should be considered and in which order they should be invoked.

1. Procedural versus Declarative Knowledge

These two types of knowledge were defined in earlier slides.

■ Procedural Knowledge :

Includes : rules, strategies, agendas, procedures, models. These explains what to do in order to reach a certain conclusion. Example

Rule: To determine if Peter or Robert is older, first find their ages.

It is knowledge about 'how to do' something. It manifests itself in the doing of something, e.g., manual or mental skills cannot reduce to words. It is held by individuals in a way which does not allow it to be communicated directly to other individuals.

Accepts a description of the steps of a task or procedure. It Looks similar to declarative knowledge, except that tasks or methods are being described instead of facts or things.

■ Declarative Knowledge : knowing 'what',  knowing 'that'

Includes : concepts, objects, facts, propositions, assertions, models.

It is knowledge about facts and relationships, that

can be expressed in simple and clear statements,

can be added and modified without difficulty.

Examples :  A car has four tyres;               Peter is older than Robert.

Declarative knowledge and explicit knowledge are articulated knowledge and may be treated as synonyms for most practical purposes. Declarative knowledge is represented in a format that can be manipulated, decomposed and analyzed independent of its content.

Comparison :

Comparison between Procedural and Declarative Knowledge :

Comparison :

Comparison between Procedural and Declarative Language :

2. Logic Programming

Logic programming offers a formalism for specifying a computation in terms of logical relations between entities.

logic program is a collection of logic statements.

 programmer describes all relevant logical relationships between the various entities.

computation determines whether or not, a particular conclusion follows from those logical statements.

Characteristics of Logic program

Logic program is characterized by set of relations and inferences. − program consists of a set of axioms and a goal statement.

rules of inference determine whether the axioms are sufficient to ensure the truth of the goal statement.

execution of a logic program corresponds to the construction of a proof of the goal statement from the axioms.

programmer specify basic logical relationships, does not specify the manner in which inference rules are applied.

Thus Logic + Control = Algorithms

Examples of Logic Statements

Statement

A grand-parent is a parent of a parent.

Statement expressed in more closely related logic terms as A person is a grand-parent if she/he has a child and that child is a parent.

Statement expressed in first order logic as

(for all) x: grandparent (x, y) :- parent (x, z), parent (z, y)

read as x is the grandparent of y

if x is a parent of z and z is a parent of y

Logic Programming Language

A programming language includes :

the syntax

the semantics of programs and

the computational model.

There are many ways of organizing computations. The most familiar paradigm is procedural. The program specifies a computation by saying

"how" it is to be performed. FORTRAN, C, and Object-oriented languages fall under this general approach.

Another paradigm is declarative. The program specifies a computation by giving the properties of a correct answer. Prolog and logic data language (LDL) are examples of declarative languages, emphasize the logical properties of a computation.

Prolog and LDL are called logic programming languages.

PROLOG (PROgramming LOGic) is the most popular Logic programming language rose within the realm of Artificial Intelligence (AI). It became popular with AI resea hers, who know more about "what" and "how" intelligent behavior is achieved.

Syntax and Terminology (relevant to Prolog programs)

In any language, the formation of components (expressions, statements,

etc.), is guided by syntactic rules.

The components are divided into two parts:

data components and (B) program components.

Data components :

Data components are collection of data objects that follow hiera hy.

All these data components are explained in next slide.

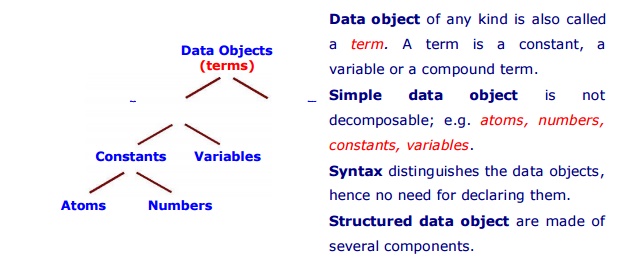
Data Objects :

The data objects of any kind is called a term.

◊ Term : Examples

‡ Constants:

Denote elements such as integers, floating point, atoms.

‡ Variables:

Denote a single but unspecified element; symbols for variables begin with an uppe ase letter or an underscore.

‡ Compound terms:

Comprise a functor and sequence of one or more compound terms called arguments.

► Functor: is characterized by its name and number of arguments; name is an atom, and number of arguments is

arity.

ƒ/n = ƒ( t₁ , t₂, . . . t_n )

where ƒ is name of the functor and is of arity n t i

's are the argument

ƒ/n                                               denotes functor ƒ of arity n

Functors with same name but different arities are distinct.

‡ Ground and non-ground:

Terms are ground if they contain no variables (only constant signs); otherwise they are non-ground.

Goals are atoms or compound terms, and are generally non-ground.

Simple Data Objects : Atoms, Numbers, Variables

◊  Atoms

‡                          a lower-case letter, possibly followed by other letters of either case, digits, and underscore character.

e.g.                                 a           greaterThan      two_B_or_not_2_b

‡ a string of special characters such as: + - * / \ = ^ < > : ~ # $ &

e.g. <> ##&& ::=

‡ a string of any characters enclosed within single quotes.

e.g. 'ABC' '1234' 'a<>b'

‡ following are also atoms !               ;  []  {}

Numbers

applications involving heavy numerical calculations are rarely written in Prolog.

‡     integer  representation:  e.g. 0      -16  33    +100

‡     real numbers  written in standard or scientific notation,

e.g.  0.5  -3.1416   6.23e+23 11.0e-3   -2.6e-2

Variables

begins by a capital letter, possibly followed by other letters of either case, digits, and underscore

character. e.g. X25 List Noun_Phrase

Structured Data Objects : General Structures , Special Structures

.

General Structures

a structured term is syntactically formed by a functor and a list of arguments.

functor is an atom.

list of arguments appear between parentheses.

arguments are separated by a comma.

each argument is a term (i.e., any Prolog data object).

the number of arguments of a structured term is called its arity.

‡ e.g.  greaterThan(9, 6)          f(a, g(b, c), h(d))   plus(2, 3, 5)

Note : a structure in Prolog is a mechanism for combining terms together, like integers 2, 3, 5 are combined with the functor plus.

Special Structures

In Prolog an ordered collection of terms is called  a list .

‡ Lists are structured terms and Prolog offers a              convenient

notation to represent them:

Empty list is denoted by the atom [ ].

Non-empty list carries element(s) between square brackets,

separating elements by comma.

e.g.                                  [bach, bee] [apples, oranges, grapes]

Program Components

A Prolog program is a collection of predicates or rules.

A predicate establishes a relationships between objects.

Clause, Predicate, Sentence, Subject

Clause is a collection of grammatically-related words .

Predicate is composed of one or more clauses.

Clauses are the building blocks of sentences; every sentence contains one or more clauses.

A Complete Sentence has two parts: subject and predicate. o subject is what (or whom) the sentence is about.

predicate tells something about the subject.

Example 1 :  "cows eat grass".

It is a clause, because it contains the subject "cows" and the predicate "eat grass."

Example 2 :  "cows eating grass are visible from highway"

This is a complete clause.

the subject "cows eating grass"  and the predicate "are visible from the highway" makes complete thought.

(b) Predicates        & Clause

Syntactically                     a predicate is composed of one or more clauses.

‡ The general form of clauses is

<left-hand-side> :- <right-hand-side>.

where LHS  is a single goal called "goal"                 and RHS is composed of one or more goals, separated by commas,  called "sub-goals" of the goal on left-hand side.

The symbol " :- " is pronounced as "it is the case"          or "such that"

‡ The structure of a clause in logic program

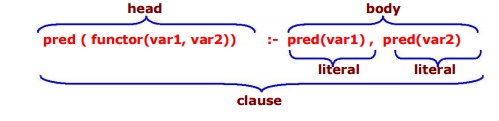
Literals represent the possible choices in primitive types the particular language. Some of the choices of types of literals are often integers, floating point, Booleans and character strings.

‡ Example :                         grand_parent (X, Z) :- parent(X, Y), parent(Y, Z).

parent (X, Y)                                            :- mother(X, Y).

parent (X, Y)                                           :- father(X, Y).

Read as if x is mother of y then x is parent of y

Interpretation:

A clause specifies the conditional truth of the goal on the LHS; goal on LHS is assumed to be true if the sub-goals on RHS are all true. A predicate is true if at least one of its clauses is true.

An individual "X" is the grand-parent of "Z"  if a parent of that same "X"  is "Y"  and "Y"  is the parent of that "Z".

Unit Clause - a special Case

Unlike the previous example of conditional truth, one often encounters unconditional relationships that hold.

In Prolog the clauses that are unconditionally true are called unit clause or fact .

Example : Unconditionally relationships say 'X' is

the father of 'Y' is unconditionally true.

This relationship as a Prolog clause is

father(X, Y) :- true.

Interpreted as relationship of father between X and Y is always true; or simply stated as X is father of Y .

Goal true is built-in in Prolog and always holds.

Prolog offers a simpler syntax to express unit clause or fact

father(X, Y)

ie  the " :- true " part is simply omitted.

Queries

In Prolog the queries are statements called directive. A special case of directives, are called queries.

Syntactically, directives are clauses with an empty left-hand side. Example : ? - grandparent(Q, Z).

This query Q is interpreted as :  Who is a grandparent of Z ?

By issuing queries Q, Prolog tries to establish the validity of specific relationships.

The answer from previous slides is (X is grand parent of Z)

The result of executing a query is either success or failure Success, means the goals specified in the query holds according to the facts and rules of the program.

Failure, means the goals specified in the query does not hold according to the facts and rules of the program.

• Programming Paradigms :       Models of Computation

A complete description of a programming language includes the computational model, syntax, semantics, and pragmatic considerations that shape the language.

Models of Computation :

A computational model is a collection of values and operations, while computation is the application of a sequence of operations to a value to yield another value.

There are three basic computational models :

(a) Imperative, (b) Functional,  and (c) Logic.

In addition to these, there are two programming paradigms :

(a) concurrent  (b) object-oriented programming .

While, these two are not models of computation, but they rank in importance with computational models.

Imperative Model

The  Imperative  model  of  computation,  consists  of  a  state  and  an operation of assignment which is   used to modify the state.

Programs consist of sequences      of commands.

Computations are changes in the state.

Example : Linear function

A linear function y = 2x + 3 can be written as

Y := 2 ∗ X + 3

The implementation requires to determines the value of X in the state and then creates a new state which differs from the old state.

New State: X = 3,  Y = 9,

The imperative model is closest to the hardware model on which programs are executed, that makes it most efficient model in terms of execution time.

Functional model

The Functional model of computation, consists of a set of values, functions, and the operation of functions. The functions may be named and composed with other functions. It can take other functions as arguments and return results.

Programs consist of definitions of functions. Computations are application of functions to values.

‡ Example 1 : Linear function

A linear function y = 2x + 3 can be defined as : f (x) = 2 ∗ x + 3

‡ Example 2 : Determine a value for Ci           umference.

Assign a value to Radius, that determines a value for Ci     umference.

Ci                                  umference = 2 × pi × radius ,   where pi = 3.14

Generalize Ci                          umference with the variable "radius"    ie

Ci                                  umference(radius) = 2 × pi × radius , where pi = 3.14

Functional models are developed over many years. The notations and methods form the base upon which problem solving methodologies rest.

Logic Model

The logic model of computation is based on relations and logical inference.

Programs consist of definitions of relations.

Computations are inferences (is a proof).

‡ Example 1 : Linear function

A linear function y = 2x + 3 can be represented as :

f (X , Y) if                                  Y is  2 ∗  X + 3.

Here the function represents the relation between X and Y.

‡                      Example 2: Determine a value for Ci  umference.

The ci                            umference computation can be represented

as:

Ci                                         le (R , C) if Pi = 3.14 and C = 2 ∗  pi ∗  R.

Here the function is represented as the relation between radius R and ci umference C.

Example 3: Determine the mortality of Socrates and Penelope. The program is to determine the mortality of Socrates and Penelope.

The fact given that Socrates and Penelope are human.

The rule is that all humans are mortal, that is

for all X, if X is human then X is mortal.

To determine the mortality of Socrates or Penelope, make the

assumption that there are no mortals, that is

KR – Logic - models of computation

‡ The equivalent form of the facts and rules stated before are

human (Socrates)

mortal (X) if human (X)

To determine the mortality of Socrates and Penelope, we made the assumption that there are no mortals i.e. ¬ mortal (Y)

Computation (proof) that Socrates is mortal

Explanation :

The 1st line is the statement "Socrates is a man." *

The 2nd line is a phrase "all human are mortal"

into the equivalent  "for all X,  if X is a man then X is mortal".

The 3rd line is added to the set to determine the mortality of Socrates.

The 4th line is the deduction from lines 2 and 3. It is justified by the inference rule modus tollens which states that if the conclusion of a rule is known to be false, then so is the hypothesis.

Variables X and Y are unified because they have same value.

By unification, Lines 5, 4b, and 1 produce contradictions and identify Socrates as mortal.

Note that, resolution is an inference rule which looks for a contradiction and it is facilitated by unification which determines if there is a substitution which makes two terms the same.

Logic model formalizes the reasoning process. It is related to relational data bases and expert systems.

3. Forward versus Backward Reasoning

Rule-Based system a hitecture consists a set of rules, a set of facts, and

an inference engine. The need is to find what new facts can be derived.

Given a set of rules, there are essentially two    ways  to generate new

knowledge: one, forward chaining and the other,  backward chaining.

■                Forward chaining : also called data driven.

It starts with the facts, and sees what rules apply.

■                Backward chaining : also called goal driven.

It starts with something to find out, and looks for rules that will help in answering it.

■ Example 3 : A typical Forward Chaining

■ Example 4 : A typical Backward Chaining

Forward Chaining

The Forward chaining system, properties , algorithms, and conflict resolution strategy are illustrated.

■  Forward chaining system

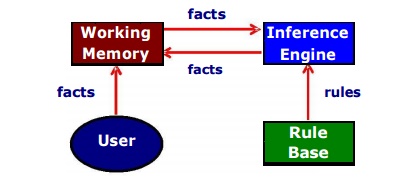
facts are held in a working memory

condition-action rules represent actions to be taken when specified facts occur in working memory.

typically, actions involve adding or deleting facts from the working memory.

Properties of Forward Chaining

all rules which can fire do fire.

can be inefficient - lead to spurious rules firing, unfocused problem solving

set of rules that can fire known as conflict set.

decision about which rule to fire is conflict resolution.

■  Forward chaining algorithm – I

Apply on the Example 2 extended (adding 2 more rules and 1 fact)

Now,  two rules can fire (R2 and R4)

■ Forward chaining algorithm - II (applied to example 2 above )

Repeat

Collect the rules whose conditions match facts in WM.

If more than one rule matches as stated above then

◊ Use conflict resolution strategy to eliminate all but one

‡ Do actions indicated by the rules

(add facts to WM or delete facts from WM)

Until problem is solved or no condition match

Conflict Resolution Strategy

Conflict set is the set of rules that have their conditions satisfied by working memory elements.

Conflict resolution normally selects a single rule to fire. The popular conflict resolution mechanisms are :

Refractory,  Recency, Specificity.

Refractory

a rule should not be allowed to fire more than once on the same data.

discard executed rules from the conflict set.

prevents undesired loops.

Recency

rank instantiations in terms of the recency of the elements in the premise of the rule.

rules which use more recent data are preferred.

working memory elements are time-tagged indicating at what cycle each fact was added to working memory.

Specificity

rules which have a greater number of conditions and are therefore more difficult to satisfy, are preferred to more general rules with fewer conditions.

more specific rules are „better‟ because they take more of the data into account.

Alternative to Conflict Resolution – Use Meta Knowledge

Instead of conflict resolution strategies, sometimes we want to use knowledge in deciding which rules to fire. Meta-rules reason about which rules should be considered for firing. They direct reasoning rather than actually performing reasoning.

to guide sea

Meta-knowledge : knowledge about knowledge h.

Example of meta-knowledge

IF                                         conflict set contains any rule (c , a)  such that

a = "animal is mammal''

THEN                                  fire (c , a)

‡                      This example says meta-knowledge encodes knowledge about how to guide sea h for solution.

Meta-knowledge, explicitly coded in the form of rules with "object level" knowledge.

Backward Chaining

Backward chaining system and the algorithm are illustrated.

Backward chaining system

‡                      Backward chaining means reasoning from goals back to facts. The idea is to focus on the sea h.

Rules and facts are processed using backward chaining interpreter.

Checks hypothesis, e.g. "should I switch the sprinklers on?"

Backward chaining algorithm

Prove goal G

If   G  is in the initial facts , it is proven.

Otherwise, find a rule which can be used to conclude G, and try to prove each of that rule's conditions.

Forward vs Backward Chaining

Depends on problem, and on properties of rule set.

Backward chaining is likely to be better if there is clear hypotheses. Examples : Diagnostic problems or classification problems, Medical expert systems

Forward chaining may be better if there is less clear hypothesis and want to see what can be concluded from current situation;

Examples :  Synthesis systems - design / configuration.

4. Control Knowledge

An algorithm consists of : logic component, that specifies the knowledge to be used in solving problems, and control component, that determines the problem-solving strategies by means of which that knowledge is used.

Thus Algorithm = Logic + Control .

The logic component determines the meaning of the algorithm whereas the control component only affects its efficiency.

An algorithm may be formulated in different ways, producing same behavior. One formulation, may have a clear statement in logic component but employ a sophisticated problem solving strategy in the control component. The other formulation, may have a complicated logic component but employ a simple problem-solving strategy.

The efficiency of an algorithm can often be improved by improving the control component without changing the logic of the algorithm and therefore without changing the meaning of the algorithm.

The trend in databases is towards the separation of logic and control. The programming languages today do not distinguish between them. The programmer specifies both logic and control in a single language. The execution mechanism exe ises only the most rudimentary problem-solving capabilities.

Computer programs will be more often correct, more easily improved, and more readily adapted to new problems when programming languages separate logic and control, and when execution mechanisms provide more powerful problem-solving facilities of the kind provided by intelligent theorem-proving systems.