Predicate Calculus

Predicate Calculus

First-order logic

Whereas propositional logic assumes the world contains facts,

first-order logic (like natural language) assumes the world contains

Objects: people, houses, numbers, colors, baseball games, wars, …

Relations: red, round, prime, brother of, bigger than, part of, comes between, …

Syntax of FOL: Basic elements

•        Constants   TaoiseachJohn, 2, DIT,...

•        Predicates   Brother, >,...

•        Functions   Sqrt, LeftLegOf,...

•        Variables    x, y, a, b,...

•        Connectives         ,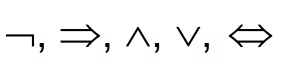   

•        Equality     =

•        Quantifiers ,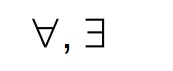 

Atomic sentences

Atomic sentence =                            predicate (term₁,...,term_n)

or term₁ = term₂

Term                              =                 function (term₁,...,term_n)

or constant or variable

E.g., Brother(TaoiseachJohn,RichardTheLionheart) > (Length(LeftLegOf(Richard)), Length(LeftLegOf(TaoiseachJohn)))

Complex sentences 

Complex sentences are made from atomic sentences using connectives

Truth in first-order logic

Sentences are true with respect to a model and an interpretation

Model contains objects (domain elements) and relations among them

Interpretation specifies referents for

constant symbols →      objects

predicate symbols         →      relations

function symbols →      functional relations

An atomic sentence predicate(term₁,...,term_n) is true iff the objects referred to by term₁,...,term_n

are in the relation referred to by predicate

Universal quantification

Roughly speaTaoiseach, equivalent to the conjunction of instantiations of P

At(TaoiseachJohn,DIT) -- >  Smart(TaoiseachJohn)

At(Richard,DIT) -- > Smart(Richard)

At(DIT,DIT)         -- > Smart(DIT)

A common mistake to avoid

means “Everyone is at DIT and everyone is smart”

Existential quantification

Roughly speaTaoiseach, equivalent to the disjunction of instantiations of P

At(TaoiseachJohn,DIT) -- > Smart(TaoiseachJohn)

At(Richard,DIT)   -- > Smart(Richard)

At(DIT,DIT)         -- > Smart(DIT)

Another common mistake to avoid

Properties of quantifiers

Equality

term₁ = term₂ is true under a given interpretation if and only if term₁ and term₂ refer to the same object

E.g., definition of Sibling in terms of Parent:

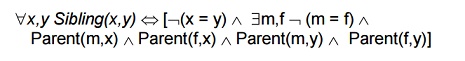
Using FOL

The kinship domain:

Brothers are siblings

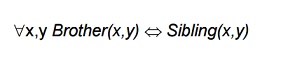
One's mother is one's female parent

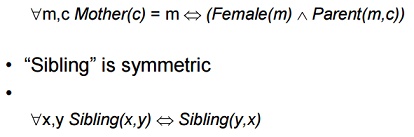
“Sibling” is symmetric

Knowledge engineering in FOL

·        Identify the task

·        Assemble the relevant knowledge

·        Decide on a vocabulary of predicates, functions, and constants

·        Encode general knowledge about the domain

·        Encode a description of the specific problem instance

·        Pose queries to the inference procedure and get answers

·        Debug the knowledge base

Summary

First-order logic:

objects and relations are semantic primitives

syntax: constants, functions, predicates, equality, quantifiers

Semantics for Predicate Calculus

An interpretation over D is an assignment of the entities of D to each of the constant, variable, predicate and function symbols of a predicate calculus expression such that:

1: Each constant is assigned an element of D

2: Each variable is assigned a non-empty subset of D;(these are the allowable substitutions for that variable)

3: Each predicate of arity n is defined on n arguments from D and defines a mapping from Dⁿ into {T,F}

4: Each function of arity n is defined on n arguments from D and defines a mapping from Dⁿ into D

The meaning of an expression

Given an interpretation, the meaning of an expression is a truth value assignment over the interpretation.

Truth Value of Predicate Calculus expressions

Assume an expression E and an interpretation I for E over a non empty domain D. The truth value for E is determined by:

The value of a constant is the element of D assigned to by I

The value of a variable is the set of elements assigned to it by I

More truth values

The value of a function expression is that element of D obtained by evaluating the function for the argument values assigned by the interpretation

The value of the truth symbol “true” is T

The value of the symbol “false” is F

The value of an atomic sentence is either T or F as determined by the interpretation I

Similarity with Propositional logic truth values

The value of the negation of a sentence is F if the value of the sentence is T and F otherwise

The values for conjunction, disjunction ,implication and equivalence are analogous to their propositional logic counterparts

Universal Quantifier

The value for

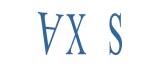
Is T if S is T for all assignments to X under I, and F otherwise

Existential Quantifier

The value for

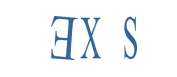
Is T if S is T for any assignment to X under I, and F otherwise

Some Definitions

A predicate calculus expressions S1 is satisfied.

Definition If there exists an Interpretation I and a variable assignment under I which returns a value T for S1 then S1 is said to be satisfied under I.

S is Satisfiable if there exists an interpretation and variable assignment that satisfies it: Otherwise it is unsatisfiable

A set of predicate calculus expressions S is satisfied.

Definition For any interpretation I and variable assignment where a value T is returned for every element in S the the set S is said to be satisfied,

A set of expressions is satisfiable if and only if there exist an intrepretation and variable assignment that satisfy every element

If a set of expressions is not satisfiable, it is said to be inconsistent

If S has a value T for all possible interpretations , it is said to be valid

A predicate calculus expressions S1 is satisfied.

Definition If there exists an Interpretation I and a variable

assignment under I which returns a value T for S1 then S1 is

said to be satisfied under I.

A set of predicate calculus expressions S is satisfied.

Definition For any interpretation I and variable assignment

where a value T is returned for every element      in S the the set

S is said to be satisfied,

An inference rule is complete.

Definition If all predicate calculus expressions X that logically

follow from a set of expressions, S can be produced using the

inference rule , then the inference rule is said to be complete.

A predicate calculus expression X logically follows from a set S of predicate calculus expressions .

For any interpretation I and variable assignment where S is satisfied, if X is also satisfied under the same interpretation and variable assignment then X logically follows from S.

Logically follows is sometimes called entailment

Soundness

An inference rule is sound.

If all predicate calculus expressions X produced using the inference rule from a set of expressions, S logically follow from S then the inference rule is said to be sound.

Completeness

An inference Rule is complete if given a set S of predicate calculus expressions, it can infer every expression that logically follows from S