AI Resolution: Definition and Principle

RESOLUTION

Problem Definition

Input

1.      Database containing formally represented facts: First-order logic sentences converted into clause form.

2.      Inference rule: Resolution principle (MP & MT)

Goal: An inference procedure

Requirements:

a.     Soundness – every sentence produced by the procedure will be “true”.

b.     Completeness – every “true” sentence can be produced by the procedure

Definitions

·        Terms:

–       Constants (e.g. “c1”, “c2”)

–       Variables (e.g. “x1”, “x2”)

–       Functions (e.g. “f(x1, x2)”)

·        Predicate – Indicator function on terminals.

– e.g. EVEN(t) : Numbers   {TRUE, FALSE}

·        Atom – the application of a predicate on a literal.

e.g. EVEN(t)

·        Literal – A predicate or its negation

e.g. EVEN(t), ¬EVEN(t)

Deinitions

·        Formulae – Recursively defined:

Every Atom is a formula

If  w1, w2  are formulae, then so are:

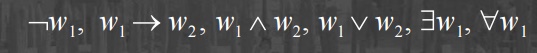
·        Clause – Disjunction (or) of literals.

The Resolution Principle

Given:

A clause Φ containing the literal: φ

A clause Ψ containing the literal: ¬φ

We can conclude:

(Φ – {φ}) U (Ψ – {¬φ})

Given:

o   A clause Φ containing the literal: φ

o   A clause Ψ containing the literal: ¬ψ

– A most general unifier g       of φ and ¬ ψ

We can conclude:

((Φ – {φ}) U (Ψ – {¬ψ}))  |  g

Let DB be a set of true sentences without contradictions, and C be a sentence we want to prove.

The Idea - proof by negation:

Assume ¬C and try to find a contradiction.

Intuition

If all DB sentences are true, and assuming ¬ C creates a contradiction then C must be inferred from DB.

o   Convert:  DB U {¬C}  to clause form.

o   If there is a contradiction in DB, C was proved. Terminate.

o   Select two clauses and add their resolvents to the current DB. If there are no resolvable clauses – the procedure fails, terminate. Else, go to step 2.

Conversion to Clause Form

1.     Eliminate all   $:

Replace A $B with ¬A V B

2.     Distribute negations:

Replace ¬¬A with A

 …

3.     Eliminate existential quantifiers by replacing with Skölem constants or functions:

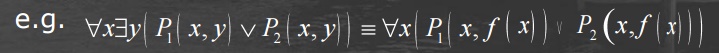
4.     Rename variables to avoid duplicates between different quantifiers.

5.     Drop all universal quantifiers

6.     Put expression into conjunctive normal form (CNF).

7.     Convert to clauses (sets of literals).

8.     Rename variables to avoid duplicates between different clauses.

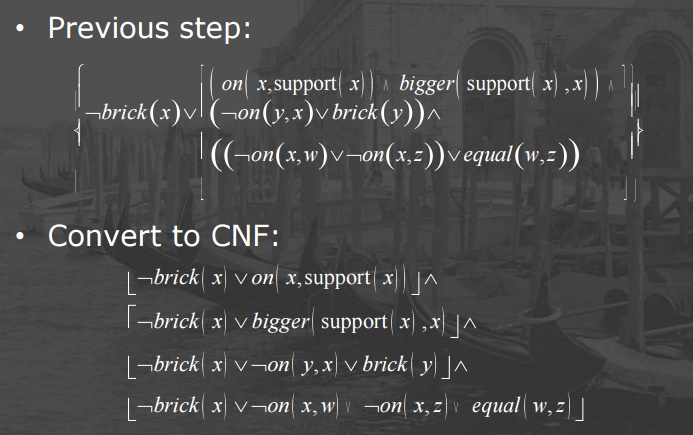
Simple Example

·        The problem:

“Heads I win, tails you lose.”

Use resolution to show I always win.