Chapter: Artificial Intelligence
Structures used in Matching
Structures used in Matching
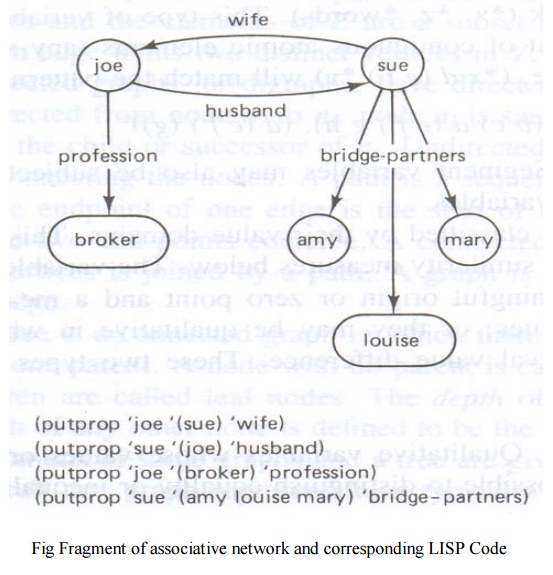
The types of list structures represent clauses in
propositional or predicate logic such as (or ~(MARRIED ?x ?y) ~(DAUGHTER ?z ?y)
(MOTHER ?y ?z)) or rules such as (and ((cloudy-sky) (low-bar-pressure)
(high-humidity)) (conclude (rain likely)) or fragments of associative networks
in below Fig
The other common structures include strings of
characters a1 a2 . . . ak , where the ai
belong to given alphabet A, vector X = (x1 x2 . . . xn),
where the xi represents attribute values, matrices M (rows of
vectors), general graphs, trees and sets
Variables
The structures are constructed from basic atomic
elements, numbers and characters
Character string elements may represent either
constants or variables
If variables, they may be classified by either the
type of match permitted or their value domains
An open variable can be replaced by a single item
Segment variable can be replaced by zero or more
items
Open variable are replaced with a preceding
question mark (?x. ?y, ?class)
They may match or assume the value of any single
string element or word, but they are subject to consistency constraints
For example, to be consistent, the variable ?x can
be bound only to the same top level element in any single structure
Thus (a ?x d ?x e) may match (a b d b e), but not
(a b d a e)
Segment variable types will be preceded with an
asterisk (*x, *z, *words)
This type of variable can match an arbitrary number
or segment of contiguous atomic elements
For example, (* x d (e g) *y) will match the
patterns
(a (b c) d (e f) g h), (d (e f ) (g))
Subject variable may also be subject to consistency
constraints similar to open variables
Nominal variables
Qualitative variables whose values or states have
no order nor rank
It is possible to distinguish between equality or
inequality between two objects
Each state can be given a numerical code
For example, “marital status” has states of
married, single, divorced or widowed. These states could be assigned numerical
codes, such as married = 1, single = 2, divorced = 3 and widowed = 4
Ordinal variables
Qualitative variables whose states can be arranged
in a rank order
It may be assigned numerical values
Foe example, the states very tall, tall, medium,
short and very short can be arranged in order from tallest to shortest and can
be assigned an arbitrary scale of 5 to 1
Binary variable
Qualitative discrete variables which may assume
only one of two values, such as 0 or 1, good or bad, yes or no, high or low
Interval variables or Metric variables
Qualitative variables which take on numeric values
and for which equal differences between values have the same significance
For example, real numbers corresponding to
temperature or integers corresponding to an amount of money are considered as
interval variables
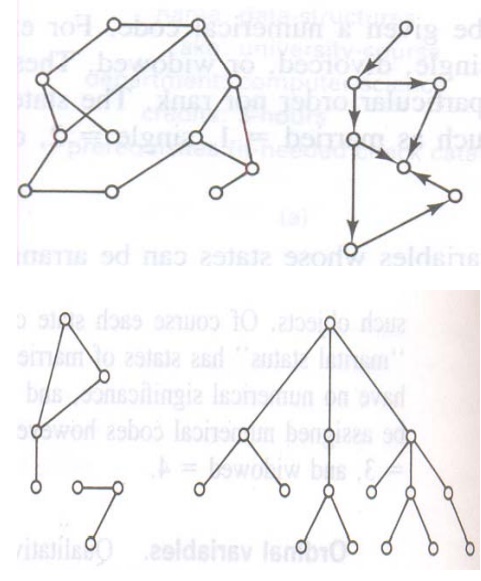
Graphs and Trees
A graph is a collection of points called vertices,
some of which are connected by line segments called edges
Graphs are used to model a wide variety of
real-life applications, including transportation and communication networks,
project scheduling, and games
A graph G = (V, E) is an ordered pair of sets V and
E. the elements V are nodes or vertices and the elements of E are a subset of V
X V called edges
An edge joints two distinct vertices in V
Directed graphs or digraphs, have directed edges or
arcs with arrows
If an arc is directed from node ni to nj
, node ni is said to be a parent or successor of nj and nj
is the child or successor of ni
Undirected graphs have simple edges without arrows
connecting the nodes
A path is a sequence of edges connecting two modes
where the endpoint of one edge is the start of its successor
A cycle is a path in which the two end points
coincide
A Connected graph is a graph for which every pair
of vertices is joined by a path
A graph is complete if every element of V X V is an
edge
A tree is a connected graph in which there are no
cycles and each node has at most one parent below
A node with no parent is called root node
A node with no children is called leaf node
The depth of the root node is defined as zero
The depth of any other node is defined to be the
depth of its parent plus 1
Sets and Bags
A set is represented as an unordered list of unique
elements such as the set (a d f c) or (red blue green yellow)
A bag is a set which may contain more than one copy
of the same member a, b, d and e
Sets and bags are structures used in matching
operations
Related Topics