Matching techniques

Matching techniques:

Matching is the process of comparing two or more structures to discover their likenesses or differences. The structures may represent a wide range of objects including physical entities, words or phrases in some language, complete classes of things, general concepts, relations between complex entities, and the like. The representations will be given in one or more of the formalisms like FOPL, networks, or some other scheme, and matching will involve comparing the component parts of such structures.

Matching is used in a variety of programs for different reasons. It may serve to control the sequence of operations, to identify or classify objects, to determine the best of a number of different alternatives, or to retrieve items from a database. It is an essential operation such diverse programs as speech recognition, natural language understanding, vision, learning, automated reasoning, planning, automatic programming, and expert systems, as well as many others.

In its simplest form, matching is just the process of comparing two structures or patterns for equality. The match fails if the patterns differ in any aspect. For example, a match between the two character strings acdebfba and acdebeba fails on an exact match since the strings differ in the sixth character positions.

In more complex cases the matching process may permit transformations in the patterns in order to achieve an equality match. The transformation may be a simple change of some variables to constants, or ti may amount to ignoring some components during the match operation. For example, a pattern matching variable such as ?x may be used to permit successful matching between the two patterns (a b (c d ) e) and (a b ?x e) by binding ?x to (c, d). Such matching are usually restricted in some way, however, as is the case with the unification of two classes where only consistent bindings are permitted. Thus, two patterns such as

( a b (c d) e f) and (a b ?x e ?x)

would not match since ?x could not be bound to two different constants.

In some extreme cases, a complete change of representational form may be required in either one or both structures before a match can be attempted. This will be the case, for example, when one visual object is represented as a vector of pixel gray levels and objects to be matched are represented as descriptions in predicate logic or some other high level statements. A direct comparison is impossible unless one form has been transformed into the other.

In subsequent chapters we will see examples of many problems where exact matches are inappropriate, and some form of partial matching is more meaningful. Typically in such cases, one is interested in finding a best match between pairs of structures. This will be the case in object classification problems, for example, when object descriptions are subject to corruption by noise or distortion. In such cases, a measure of the degree of match may also be required.

Other types of partial matching may require finding a match between certain key elements while ignoring all other elements in the pattern. For example, a human language input unit should be flexible enough to recognize any of the following three statements as expressing a choice of preference for the low-calorie food item

I prefer the low-calorie choice.

I want the low-calorie item

The low-calorie one please.

Recognition of the intended request can be achieved by matching against key words in a template containing “low-calorie” and ignoring other words except, perhaps, negative modifiers.

Finally, some problems may obviate the need for a form of fuzzy matching where an entity’s degree of membership in one or more classes is appropriate. Some classification problems will apply here if the boundaries between the classes are not distinct, and an object may belong to more than one class.

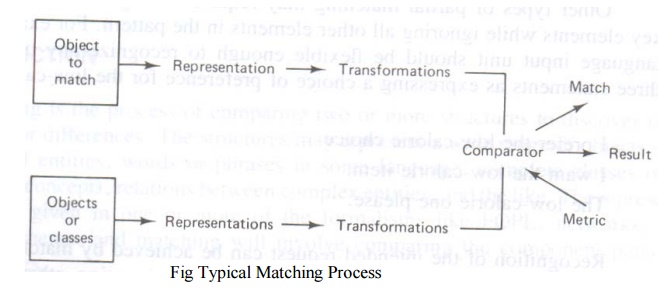
Fig 8.1 illustrates the general match process where an input description is being compared with other descriptions. As stressed earlier, their term object is used here in a general sense. It does not necessarily imply physical objects. All objects will be represented in some formalism such a s a vector of attribute values, prepositional logic or FOPL statements, rules, frame-like structures, or other scheme. Transformations, if required, may involve simple instantiations or unifications among clauses or more complex operations such as transforming a two-dimensional scene to a description in some formal language. Once the descriptions have been transformed into the same schema, the matching process is performed element-by-element using a relational or other test (like equality or ranking). The test results may then be combined in some way to provide an overall measure of similarity. The choice of measure will depend on the match criteria and representation scheme employed.

The output of the matcher is a description of the match. It may be a simple yes or no response or a list of variable bindings, or as complicated as a detailed annotation of the similarities and differences between the matched objects.

`To summarize then, matching may be exact, used with or without pattern variables, partial, or fuzzy, and any matching algorithm will be based on such factors as

Choice of representation scheme for the objects being matched,

Criteria for matching (exact, partial, fuzzy, and so on),

Choice of measure required to perform the match in accordance with the

chosen criteria, and

Type of match description required for output.

In the remainder of this chapter we examine various types of matching problems and their related algorithms. We bin with a description of representation structures and measures commonly found in matching problems. We next look at various matching techniques based on exact, partial, and fuzzy approaches. We conclude the chapter with an example of an efficient match algorithm used in some rule-based expert systems.