Measure for Matching

Measure for Matching

The problem of comparing structures without the use of pattern matching variables. This requires consideration of measures used to determine the likeness or similarity between two or more structures

The similarity between two structures is a measure of the degree of association or likeness between the object’s attributes and other characteristics parts.

If the describing variables are quantitative, a distance metric is used to measure the proximity

Distance Metrics

Ø For all elements x, y, z of the set E, the function d is metric if and only if d(x, x) = 0

d(x,y) ≥ 0

d(x,y) = d(y,x)

d(x,y) ≤ d(x,z) + d(z,y)

The Minkowski metric is a general distance measure satisfying the above assumptions

It is given by

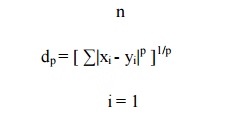
For the case p = 2, this metric is the familiar Euclidian distance. Where p = 1, d_p is the so-called absolute or city block distance

Probabilistic measures

The representation variables should be treated as random variables

Then one requires a measure of the distance between the variates, their distributions, or between a variable and distribution

One such measure is the Mahalanobis distance which gives a measure of the separation between two distributions

Given the random vectors X and Y let C be their covariance matrix

Then the Mahalanobis distance is given by

= X^’C^-1Y

Where the prime (‘) denotes transpose (row vector) and C^-1 is the inverse of C

The X and Y vectors may be adjusted for zero means bt first substracting the vector means u_x and u_y

Another popular probability measure is the product moment correlation r, given by

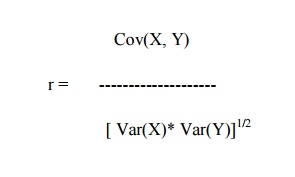
Where Cov and Var denote covariance and variance respectively

The correlation r, which ranges between -1 and +1, is a measure of similarity frequently used in vision applications

Other probabilistic measures used in AI applications are based on the scatter of attribute values

These measures are related to the degree of clustering among the objects

Conditional probabilities are sometimes used

For example, they may be used to measure the likelihood that a given X is a member of class C_i , P(C_i| X), the conditional probability of C_i given an observed X

These measures can establish the proximity of two or more objects Qualitative measures

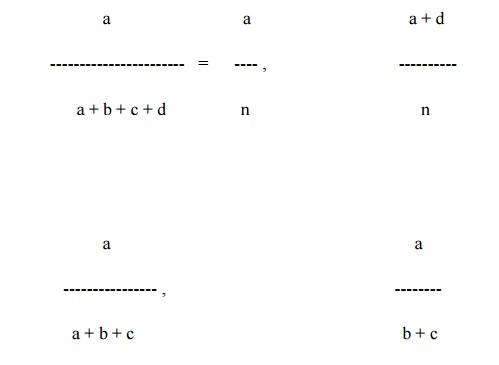
Measures between binary variables are best described using contingency tables in the below Table

The table entries there give the number of objects having attribute X or Y with corresponding value of 1 or 0

For example, if the objects are animals might be horned and Y might be long tailed. In this case, the entry a is the number of animals having both horns and long tails

Note that n = a + b + c + d, the total number of objects

Various measures of association for such binary variables have been defined

For example

Contingency tables are useful for describing other qualitative variables, both ordinal and nominal. Since the methods are similar to those for binary variables

Whatever the variable types used in a measure, they should all be properly scaled to prevent variables having large values from negating the effects of smaller valued variables

This could happen when one variable is scaled in millimeters and another variable in meters

Similarity measures

Measures of dissimilarity like distance, should decrease as objects become more alike

The similarities are not in general symmetric

Any similarity measure between a subject description A and its referent B, denoted by s(A,B), is not necessarily equal

In general, s(A,B) ≠ s(B,A) or “A is like B” may not be the same as “B is like A”

Tests on subjects have shown that in similarity comparisons, the focus of attention is on the subject and, therefore, subject features are given higher weights than the referent

For example, in tests comparing countries, statements like “North Korea is similar to Red China” and “Red China is similar to North Korea” were not rated as symmetrical or equal

Similarities may depend strongly on the context in which the comparisons are made

An interesting family of similarity measures which takes into account such factors as asymmetry and has some intuitive appeal has recently been proposed

Let O ={o₁, o₂, . . . } be the universe of objects of interest

Let A_i be the set of attributes used to represent o_i

A similarity measure s which is a function of three disjoint sets of attributes common to any two objects A_i and A_j is given as

s(A_i, A_j) = F(A_i & A_j, A_i - A_j, A_j - A_i)

Where A_i & A_j is the set of features common to both o_i and o_j

Where A_i - A_j is the set of features belonging to o_i and not o_j

Where A_j - A_i is the set of features belonging to o_j and not o_i

The function F is a real valued nonnegative function

s(A_i, A_j) = af(A_i & A_j) – bf(A_i - A_j) – cf(A_j - A_i) for some a,b,c ≥ 0

Where f is an additive interval metric function

The function f(A) may be chosen as any nonnegative function of the set A, like the number of attributes in A or the average distance between points in A

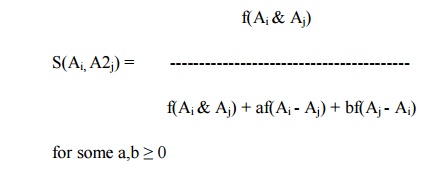
When the representations are graph structures, a similarity measure based on the cost of transforming one graph into the other may be used

For example, a procedure to find a measure of similarity between two labeled graphs decomposes the graphs into basic subgraphs and computes the minimum

cost to transform either graph into the other one, subpart-by-subpart