Feed Forward neural network

Feed Forward neural network

The neural networks consist of multiple layers of computational units, usually interconnected in a feed forward way. The feed forward neural networks are the first, simplest type of artificial neural networks devised. In this network, the information moves in only one direction, forward from the input nodes, through the hidden nodes and to the output nodes. There are no cycles or loops in the network. In other way we can say the feed forward neural network is one that does not have any connections from output to input. All inputs with variable weights are connected with every other node. A single layer feed forward network has one layer of nodes, whereas a multilayer feed forward network has multiple layers of nodes. The structure of a feed forward multilayer network is given in figure.

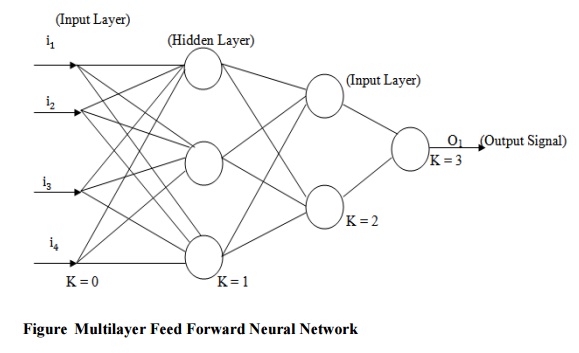
Data are introduced into the system through an input layer. This is followed by processing in one or more intermediate (hidden layers). Output data emerge from the network’s final layer. The transfer functions contained in the individual neurons can be almost anything. The input layer is also called as Zeroth layer, of the network serves to redistribute input values and does no processing. The output of this layer is described mathematically as follows.

The input to each neuron in the first hidden layer in the network is a summation all weighted connections between the input or Zeroth layer and the neuron in the first hidden layer. We will write the weighted sum as net sum or net input. We can write the net input to a neuron from the first layer as the product of that input vector i_m and weight factor w_m plus a bias term q. The total weighted input to the neuron is a summation of these individual input signals described as follows.

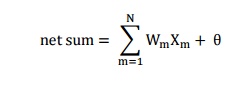
Where N represents the number of neurons in the input layer.

The net sum to the neuron is transformed by the neuron’s activation or transfer function, f to produce a new output value for the neuron. With back propagation, this transfer function is most commonly either a sigmoid or a linear function. In addition to the net sum, a bias term q is generally added to offset the input. The bias is designed as a weight coming from a unitary valued input and denoted as W₀. So, the final output of the neuron is given by the following equation.

But one question may arise in reader’s mind. Why we are using the hidden layer between the input and output layer? The answer to this question is very silly. Each layer in a multilayer neural network has its own specific function. The input layer accepts input signals from the outside world and redistributes these signals to all neurons in the hidden layer. Actually, the input layer rarely includes computing neurons and thus does not process input patterns. The output layer accepts output signals, or in other words a stimulus patterns, from the hidden layer and established the output patterns of the entire network. Neurons in the hidden layer detect the features, the weights of the neurons represent the features hidden in the input patterns. These features are then used by the output layer in determining the output patterns. With one hidden layer we can represent any continuous function of the input signals and with two hidden layers even discontinuous functions can be represented. A hidden layer hides its desired output. Neurons in the hidden layer cannot be observed through the input/ output behaviour of the network. The desired output of the hidden layer is determined by the layer itself. Generally, we can say there is no obvious way to know what the desired output of the hidden layer should be.