Examples of search problems

Examples of search problems

Traveling Salesman Problem: Given n cities with known distances between each pair, find the shortest tour that passes through all the cities exactly once before returning to the starting city.

A lower bound on the length l of any tour can be computed as follows

For each city i, 1 ≤ i ≤ n, find the sum s_i of the distances from city i to the two nearest cities.

Compute the sum s of these n numbers.

Divide the result by 2 and round up the result to the nearest integer

lb = s / 2

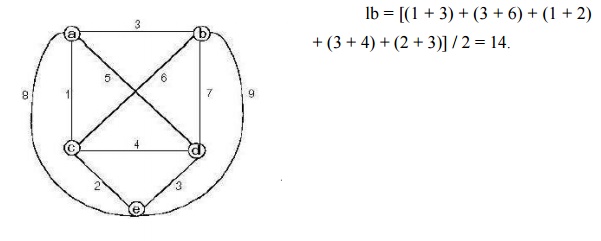
The lower bound for the graph shown in the Fig 5.1 can be computed as follows:

For any subset of tours that must include particular edges of a given graph, the lower bound can be modified accordingly. E.g.: For all the Hamiltonian circuits of the graph that must include edge (a, d), the lower bound can be computed as follows:

lb = [(1 + 5) + (3 + 6) + (1 + 2) + (3 + 5) + (2 + 3)] / 2 = 16.

Applying the branch-and-bound algorithm, with the bounding function lb = s / 2, to find the shortest Hamiltonian circuit for the given graph, we obtain the state-space tree as shown below:

To reduce the amount of potential work, we take advantage of the following two observations:

      We can consider only tours that start with a.

      Since the graph is undirected, we can generate only tours in which b is visited before c.

In addition, after visiting n – 1 cities, a tour has no choice but to visit the remaining unvisited city and return to the starting one is shown in the Fig 5.2

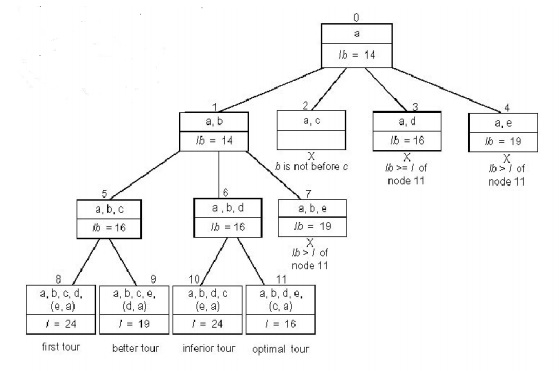
Root node includes only the starting vertex a with a lower bound of lb = [(1 + 3) + (3 + 6) + (1 + 2) + (3 + 4) + (2 + 3)] / 2 = 14.

   Node 1 represents the inclusion of edge (a, b)

lb = [(1 + 3) + (3 + 6) + (1 + 2) + (3 + 4) + (2 + 3)] / 2 = 14.

   Node 2 represents the inclusion of edge (a, c). Since b is not visited before c, this node is terminated.

   Node 3 represents the inclusion of edge (a, d)

lb = [(1 + 5) + (3 + 6) + (1 + 2) + (3 + 5) + (2 + 3)] / 2 = 16.

   Node 1 represents the inclusion of edge (a, e)

lb = [(1 + 8) + (3 + 6) + (1 + 2) + (3 + 4) + (2 + 8)] / 2 = 19.

   Among all the four live nodes of the root, node 1 has a better lower bound. Hence we branch from node 1.

   Node 5 represents the inclusion of edge (b, c)

lb = [(1 + 3) + (3 + 6) + (1 + 6) + (3 + 4) + (2 + 3)] / 2 = 16.

   Node 6 represents the inclusion of edge (b, d)

lb = [(1 + 3) + (3 + 7) + (1 + 2) + (3 + 7) + (2 + 3)] / 2 = 16.

   Node 7 represents the inclusion of edge (b, e)

lb = [(1 + 3) + (3 + 9) + (1 + 2) + (3 + 4) + (2 + 9)] / 2 = 19.

       Since nodes 5 and 6 both have the same lower bound, we branch out from each of them.

       Node 8 represents the inclusion of the edges (c, d), (d, e) and (e, a). Hence, the length of the tour,

l = 3 + 6 + 4 + 3 + 8 = 24.

       Node 9 represents the inclusion of the edges (c, e), (e, d) and (d, a). Hence, the length of the tour,

l = 3 + 6 + 2 + 3 + 5 = 19.

       Node 10 represents the inclusion of the edges (d, c), (c, e) and (e, a). Hence, the length of the tour,

l = 3 + 7 + 4 + 2 + 8 = 24.

       Node 11 represents the inclusion of the edges (d, e), (e, c) and (c, a). Hence, the length of the tour,

l = 3 + 7 + 3 + 2 + 1 = 16.

       Node 11 represents an optimal tour since its tour length is better than or equal to the other live nodes, 8, 9, 10, 3 and 4.

       The optimal tour is a → b → d → e → c → a with a tour length of 16.