AO* Search(Graph): Concept, Algorithm, Implementation, Advantages, Disadvantages

AO* Search: (And-Or) Graph

The Depth first search and Breadth first search given earlier for OR trees or graphs can be easily adopted by AND-OR graph. The main difference lies in the way termination conditions are determined, since all goals following an AND nodes must be realized; where as a single goal node following an OR node will do. So for this purpose we are using AO* algorithm.

Like A* algorithm here we will use two arrays and one heuristic function.

OPEN:

It contains the nodes that has been traversed but yet not been marked solvable or unsolvable.

CLOSE:

It contains the nodes that have already been processed.

6 7:The distance from current node to goal node.

Algorithm:

Step 1: Place the starting node into OPEN.

Step 2: Compute the most promising solution tree say T0.

Step 3: Select a node n that is both on OPEN and a member of T0. Remove it from OPEN and place it in

CLOSE

Step 4: If n is the terminal goal node then leveled n as solved and leveled all the ancestors of n as solved. If the starting node is marked as solved then success and exit.

Step 5: If n is not a solvable node, then mark n as unsolvable. If starting node is marked as unsolvable, then return failure and exit.

Step 6: Expand n. Find all its successors and find their h (n) value, push them into OPEN.

Step 7: Return to Step 2.

Step 8: Exit.

Implementation:

Let us take the following example to implement the AO* algorithm.

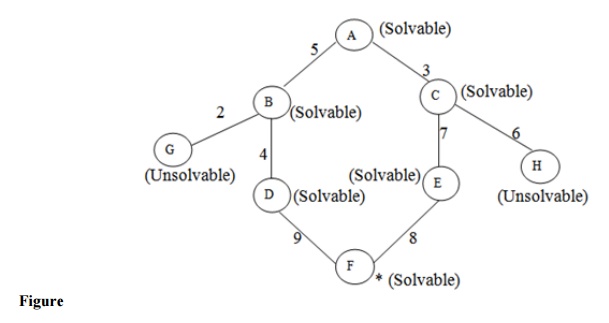
Step 1:

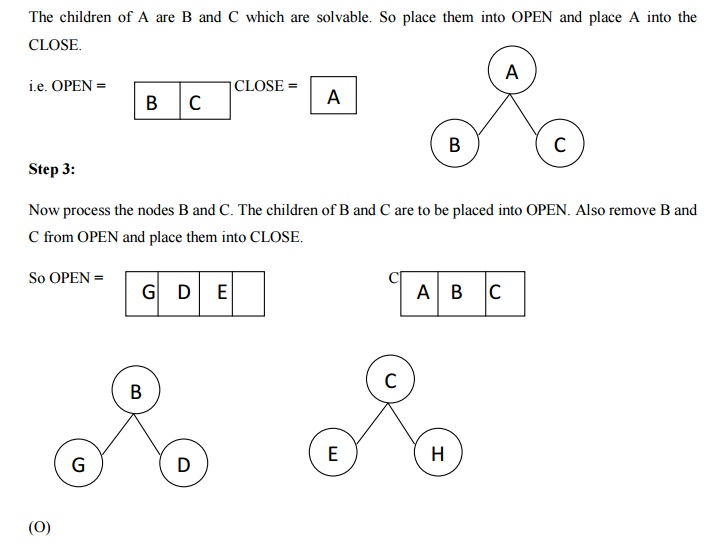
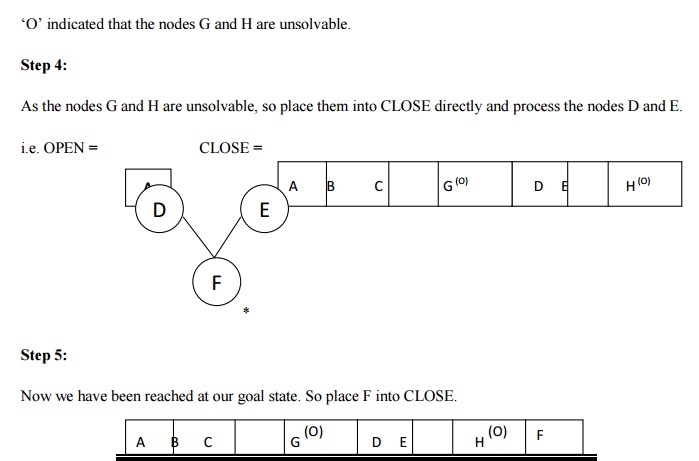
In the above graph, the solvable nodes are A, B, C, D, E, F and the unsolvable nodes are G, H. Take A as the starting node. So place A into OPEN.

Advantages:

It is an optimal algorithm.

If traverse according to the ordering of nodes. It can be used for both OR and AND graph.

Disadvantages:

Sometimes for unsolvable nodes, it can’t find the optimal path. Its complexity is than other algorithms.