A* Search: Concept, Algorithm, Implementation, Advantages, Disadvantages

A* SEARCH

A* is a cornerstone name of many AI systems and has been used since it was developed in 1968 by Peter Hart; Nils Nilsson and Bertram Raphael. It is the combination of Dijkstra’s algorithm and Best first search. It can be used to solve many kinds of problems. A* search finds the shortest path through a search space to goal state using heuristic function. This technique finds minimal cost solutions and is directed to a goal state called A* search. In A*, the * is written for optimality purpose. The A* algorithm also finds the lowest cost path between the start and goal state, where changing from one state to another requires some cost. A* requires heuristic function to evaluate the cost of path that passes through the particular state. This algorithm is complete if the branching factor is finite and every action has fixed cost. A* requires heuristic function to evaluate the cost of path that passes through the particular state. It can be defined by following formula.

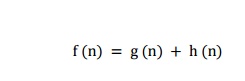
Where

g  (n) : The actual cost path from the start state to the current state. 

h ( n) : The actual cost path from the current state to goal state.

f  (n) : The actual cost path from the start state to the goal state.

For the implementation of A* algorithm we will use two arrays namely OPEN and CLOSE.

OPEN:

An array which contains the nodes that has been generated but has not been yet examined.

CLOSE:

An array which contains the nodes that have been examined.

Algorithm:

Step 1: Place the starting node into OPEN and find its f (n) value.

Step 2: Remove the node from OPEN, having smallest f (n) value. If it is a goal node then stop and return

success.

Step 3: Else remove the node from OPEN, find all its successors.

Step 4: Find the f (n) value of all successors; place them into OPEN and place the removed node into

CLOSE.

Step 5: Go to Step-2.

Step 6: Exit.

Implementation:

The implementation of A* algorithm is 8-puzzle game.

Advantages:

It is complete and optimal.

It is the best one from other techniques. It is used to solve very complex problems.

It is optimally efficient, i.e. there is no other optimal algorithm guaranteed to expand fewer nodes than A*.

Disadvantages:

This algorithm is complete if the branching factor is finite and every action has fixed cost.

The speed execution of A* search is highly dependant on the accuracy of the heuristic algorithm that is used to compute h (n).

It has complexity problems.