Hill Climbing Search Algorithm: Concept, Algorithm, Advantages, Disadvantages

Hill Climbing

Hill climbing search algorithm is simply a loop that continuously moves in the direction of increasing value. It stops when it reaches a “peak” where no n eighbour has higher value. This algorithm is considered to be one of the simplest procedures for implementing heuristic search. The hill climbing comes from that idea if you are trying to find the top of the hill and you go up direction from where ever you are. This heuristic combines the advantages of both depth first and breadth first searches into a single method.

The name hill climbing is derived from simulating the situation of a person climbing the hill. The person will try to move forward in the direction of at the top of the hill. His movement stops when it reaches at the peak of hill and no peak has higher value of heuristic function than this. Hill climbing uses knowledge about the local terrain, providing a very useful and effective heuristic for eliminating much of the unproductive search space. It is a branch by a local evaluation function. The hill climbing is a variant of generate and test in which direction the search should proceed. At each point in the search path, a successor node that appears to reach for exploration.

Algorithm:

Step 1: Evaluate the starting state. If it is a goal state then stop and return success.

Step 2: Else, continue with the starting state as considering it as a current state.

Step 3: Continue step-4 until a solution is found i.e. until there are no new states left to be applied in the current state.

Step 4:

a)    Select a state that has not been yet applied to the current state and apply it to produce a new state.

b)    Procedure to evaluate a new state.

i.     If the current state is a goal state, then stop and return success.

ii.     If it is better than the current state, then make it current state and proceed further.

iii.    If it is not better than the current state, then continue in the loop until a solution is found.

Step 5: Exit.

Advantages:

Hill climbing technique is useful in job shop scheduling, automatic programming, circuit designing, and vehicle routing and portfolio management.

It is also helpful to solve pure optimization problems where the objective is to find the best state according to the objective function.

It requires much less conditions than other search techniques.

Disadvantages:

The question that remains on hill climbing search is whether this hill is the highest hill possible. Unfortunately without further extensive exploration, this question cannot be answered. This technique works but as it uses local information that’s why it can be fooled. The algorithm doesn’t maintain a search tree, so the current node data structure need only record the state and its objective function value. It assumes that local improvement will lead to global improvement.

There are some reasons by which hill climbing often gets suck which are stated below.

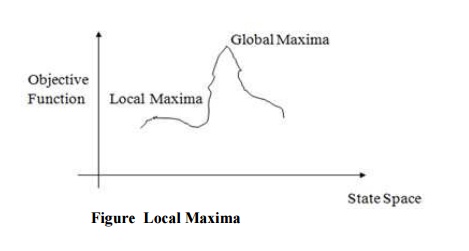
Local Maxima:

A local maxima is a state that is better than each of its neighbouring states, but not better than some other states further away. Generally this state is lower than the global maximum. At this point, one cannot decide easily to move in which direction! This difficulties can be extracted by the process of backtracking i.e. backtrack to any of one earlier node position and try to go on a different event direction. To implement this strategy, maintaining in a list of path almost taken and go back to one of them. If the path was taken that leads to a dead end, then go back to one of them.

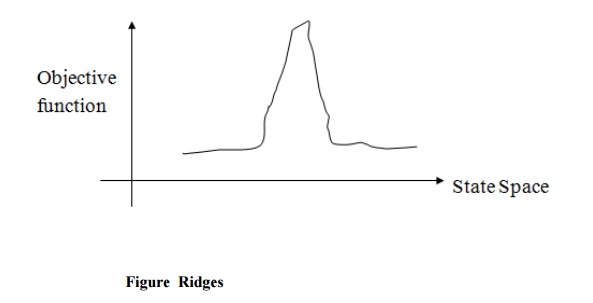
Ridges:

It is a special type of local maxima. It is a simply an area of search space. Ridges result in a sequence of local maxima that is very difficult to implement ridge itself has a slope which is difficult to traverse. In this type of situation apply two or more rules before doing the test. This will correspond to move in several directions at once.

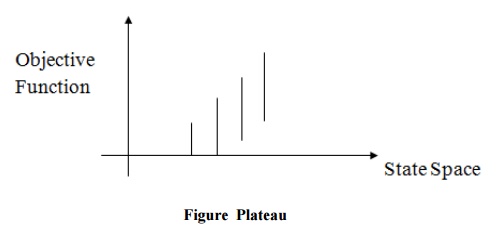
Plateau:

It is a flat area of search space in which the neighbouringhave same value. So it is very difficult to calculate the best direction. So to get out of this situation, make a big jump in any direction, which will help to move in a new direction this is the best way to handle the problem like plateau.