Response of structures to earthquakes: analysis of shear walls

Response of structures to earthquakes: analysis of shear walls

Abstract: Shear walls possess adequate lateral stiffness to reduce inter-storey distortions due to earthquake-induced motions. In this chapter, analysis of shear walls with a moment resisting frame using the Khan and Sbarounis method is discussed. When two or more shear walls are connected by a system of beams or slabs total stiffness exceeds the summation of individual stiffness. Openings normally occur in vertical rows throughout the height of the wall and the connection between wall cross-section is provided by connecting beams. Such shear walls are called coupled shear walls. The analysis of coupled shear walls by Rosman’s continuous medium method is also discussed.

Key words: shear wall, egg crate, lazy S curve, coupled shear wall, continuous medium.

Introduction

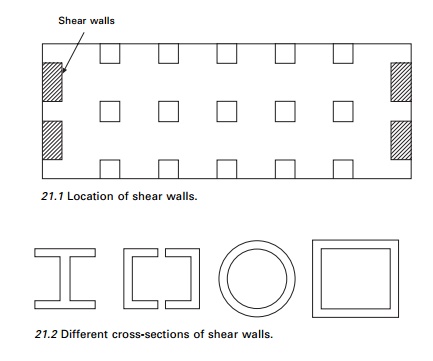
Frame action is obtained by the interaction of slabs and columns and this is not adequate to give the required lateral stiffness for buildings taller than about 15–20 storeys. Shear walls must be strategically located as shown in Fig. 21.1.

The walls can be planar, open sections or closed sections as shown in Fig. 21.2. They are provided around elevators and staircases. Shear walls of skewed and irregular layouts require 3D analysis to determine the distribution of lateral loads. The shear wall in essence behaves as a deep and slender

cantilever. When no major opening is present, stresses in the walls can be determined using simple bending theory. Complicated shapes are analysed using finite element analysis.

The term ‘shear wall’ is a misnomer as far as the high-rise building is concerned, since a slender wall when subjected to lateral force has predominant moment deflections and only very insignificant shear distortion. Major shear walls are usually positioned in the transverse direction, separating individual compartments. Stability in the longitudinal direction is provided by elevator shafts or some longitudinal shear walls. They are known as egg crate or cross-wall buildings. They are extremely rigid in the direction of shear walls.

Hence shear walls possess adequate lateral stiffness to reduce inter-storey distortions due to earthquake-induced motions. Shear walls or structural walls reduce the likelihood of damage to nonstructural elements of a building. When used with rigid frames, walls form a system that combines the gravity load-carrying efficiency of the rigid frame with the lateral load-resisting efficiency of the structural wall. Significant energy dissipation capacity lakes place. There is consistently better performance of shear wall buildings during earthquakes. They are better both with respect to life safety and damage control. Greater lateral stiffness is introduced in earthquake-resistant multi-storey shear wall buildings.

Shear wall frame

Without question this system is one of the most, if not the most, popular systems for resisting lateral loads. The system has a broad range of applications and has been used for buildings as low as 10 storeys to as high as 50 storeys or even taller buildings. With the advent of haunch girders the applicability of the system is easily extended to buildings in the 70–80 storey range.

1  Shear wall frame interaction

This interaction has been understood for quite some time. The classical mode of the interaction between a prismatic shear wall and a moment frame is shown in Fig. 21.3. The frame basically deflects in a so-called shear mode to which the shear wall predominantly responds by bending as a cantilever.

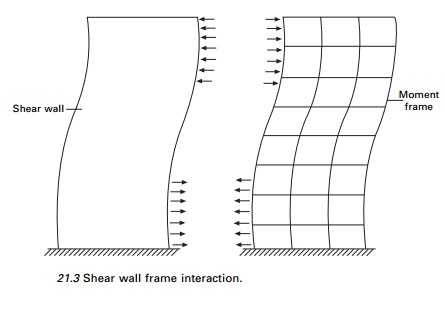
Compatibility of horizontal deflection produces interaction between the two. The linear sway of the moment frame, when combined with storey sway of shear walls, results in enhanced stiffness because the wall is restrained by the frame in the upper floor while at lower levels the frames restrained by the wall, resulting in deflected shape in the form of a ‘lazy S’ curve.

However, it is always easy to differentiate between modes. A frame with closely spaced columns with deep beams tends to behave more or less like a shear wall in bending mode, while the wall weakened by large openings tends to act more or less like a frame deflecting in shear mode. The combined structural action therefore depends on the relative rigidity of the two and their modes of deformation.

The simple interaction diagram shown in Fig. 21.3 is valid only:

•       if the shear wall and frame have constant stiffness throughout the height;

•       if stiffness varies, the relative stiffness of the wall and the frame remains unchanged throughout the height.

First consider an example of shear wall with moment resisting frame analysed by the Khan and Sbarounis (1964) method.

Example 21.1

Analyse the building shown in Fig. 21.4 for a uniform lateral load of 1.5 kN/m² which is the result of earthquake motion. All girders are 300 × 500 mm.

Solution

I_G = 8.859 × 10⁹ mm⁴ (includes slab) except 3 m link beam (250 × 400 mm size). I_LB = 3.25 × 10⁹ mm⁴ (link beams are assumed to be hinged). E (concrete) = 20 GPa.

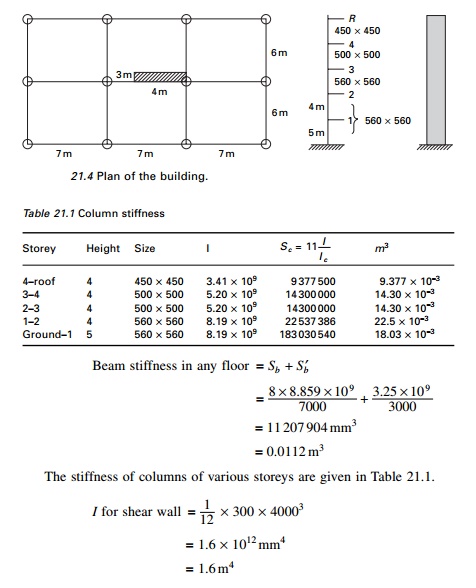
=1.6 × 10¹² mm⁴

=1.6 m⁴

Lateral load due to earthquake (for the whole frame)

On the nodes 2, 3, 4, 5 = 1.5 × 4 × 12

= 72 kN

On node 1 = 1.5 × 4.5 × 12

= 81 kN

Step 1 Estimate wall deflections. For the approximate analysis, compute deflection of the wall having I = I_w + I_c (1.6 + I_c) loaded with full lateral load. The deflection is computed using Newmark’s method. Ic is comparatively smaller and hence need not be taken into account. The calculations are shown in Fig. 21.5.

Step 2 For the frame to fit the wall and compute the moments by using anti-symmetric loading on a symmetrical structure to reduce the frame to single column frame. Distribution factors are given in Table 21.2 and shown in Fig. 21.6.

Beam stiffness = 1.5 ( S _b + S_b^′ ) = 0.0168 m³

Fixed end moment in columns due to 0.001 drift

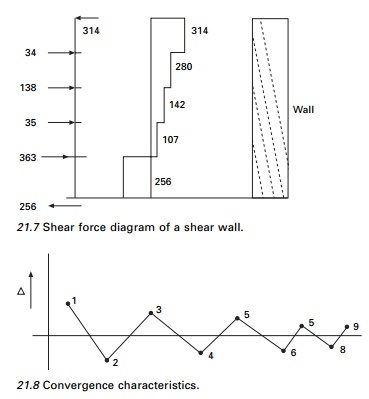
The fixed moments due to drift are shown in Table 21.3. Moment distribution is carried out as shown in Table 21.4. Now the wall has to be analysed for the loading condition as shown in Fig. 21.7. The convergence characteristics are given in Fig. 21.8. The free body diagram is shown in Fig. 21.9.

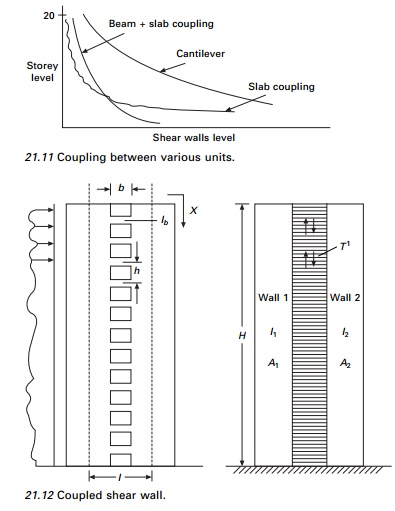
Coupled shear walls

When two or more shear walls are connected by a system of beams or slabs, total stiffness exceeds the summation of individual stiffness. This is because the connecting beam restrains individual cantilever action. Shear walls resist lateral forces up to 30–40 storeys (see Fig. 21.10). Walls with openings present a complex problem to the analyst.

Openings normally occur in vertical rows throughout the height of the wall and the connection between wall cross-sections is provided either by connecting beams which form part of the wall or floor slab or a combination of both. The terms ‘coupled shear walls’, ‘pierced shear walls’ and ‘shear wall with openings’ are commonly described for such units. If the openings are very small, their effect on the overall state of stress in the shear wall is minimal. Large openings have a pronounced effect and if large enough result in a system in which frame action predominates. The degree of coupling between two walls separated by a row of openings has been expressed of geometric parameter α (having a unit of 1/length) which it gives a measure of relative stiffness of beams with respect to that of walls. When αH exceeds 13, the walls may be analysed as a single homogenous cantilever. When αH<0.8 the wall may be analysed as the separate cantilever, 0.8<αH<13, the

stiffness of connecting beam must be considered. The effectiveness of coupling can clearly be seen in Fig. 21.11.

1.Continuous medium method due to Rosman (1966)

The individual connecting beams of finite stiffness I_b are replaced by an imaginary continuous connection or lamina. The equivalent stiffness of the lamina for a storey height h is I_b/h, giving stiffness of I_b/h dx for a height of dx (see Fig. 21.12).

When the wall is subjected to horizontal loading, the walls deflect, inducing vertical shear force in the laminas. The system is made statically determinate by introducing a cut along a centre line of beams, which is assumed to lie on the points of contra-flexure. The displacement at each wall is determined and by considering the compatibility of deformation of the lamina, a second order differential equation with the vertical shear force as a variable is established. The solution of the differential equations with fixed base boundary conditions is most common loading to an equation for the integral shear T from which the moment, axial loads in the walls can be established and all the other quantities can be written.

E       –        Modulus of elasticity

b        –        Width of opening

Ab     –        Area of connecting beam

I        –        I₁ + I₂

G       –        Shear modulus

Ib      –        Moment of inertia of connecting beam including shear deformation

d        –        depth of inter-connecting beam

ν   –  Poisson’s ratio

α, β, β, are the parameters given by following equations:

Under lateral loads the two ends of the beam experience a vertical displacement consisting of contributions δ₁, δ₂, δ₃ and δ₄ as shown in Fig. 21.13

Wall rotation

The relative displacement δ₁ due to bending of each wall element is given by

Beam bending

The shear force V = qh acting at each floor level at the centre of connecting beams with centre relations displacement δ₂

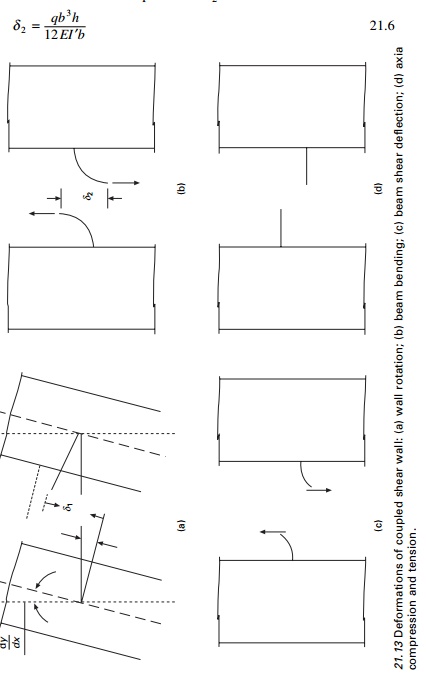
Beam shear deflection                                                   

The same shear force causes a deformation δ3 as

Axial compression and tension

The displacement δ₄ is the relative displacement of the two wall elements due to axial deformations of the walls caused by T acting as a vertical wall on the wall elements

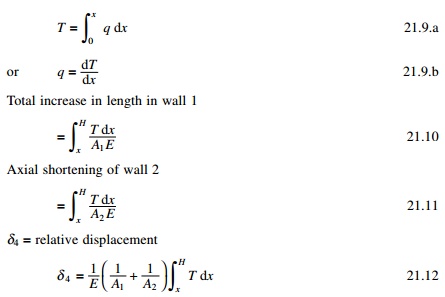
Since the two walls are connected, the compatability and stipulation that the relative displacement vanishes

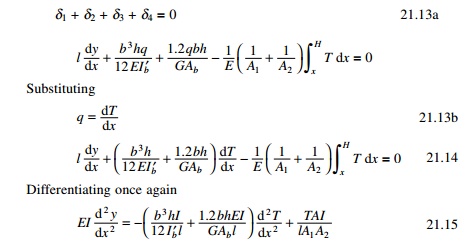
The first two terms on the right-hand side of the above equation which pertain to bending and shear deflection of the beam and can be combined to a single term by reducing moment of inertia to include shear deformation as

2 Coupled shear wall subjected to uniformly distributed load)

Once the distribution of force T has been obtained the shear force in the coupling beam may be determined as the difference in values of T at levels h/2 above below and above that level

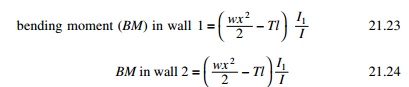
The general expression for deflection y at a point x can  be obtained by integrating with the expression

where H is measured from the top. Although inter-storey drifts are important most usually in preliminary analysis, the maximum deflection at the top is of prime interest. This is given by the following expression

To analyse a system of coupled shear wall by the method requires laborious calculation. Several researchers have proposed simplified procedures. Coull and Choudhury (1967) proposed the following method. The stress distribution of coupled shear walls is obtained as a combination of two distinct actions.

1.     Walls acting together as a single composite cantilever with neutral axis located at the centroid of two elements.

2.     Walls acting as two independent cantilever bending about their neutral axis. Semi-graphical methods are also presented for rapid design.

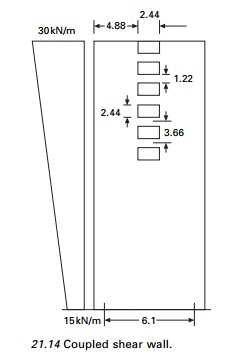
Example 21.2

Analyse the shear wall shown in Fig. 21.14. Thickness of wall = 300 mm; width of I wall = 4.88 m; width of II wall = 2.44 m  Width of opening = 2.44m.

Solution

Total width = 4.88 + 4.88 = 9.76

I = 2.44+ 2.44+ 1.22 = 6.1 m

b = 2.44 m d = 1.22 m

H = 73.152 m h = 3.66 m

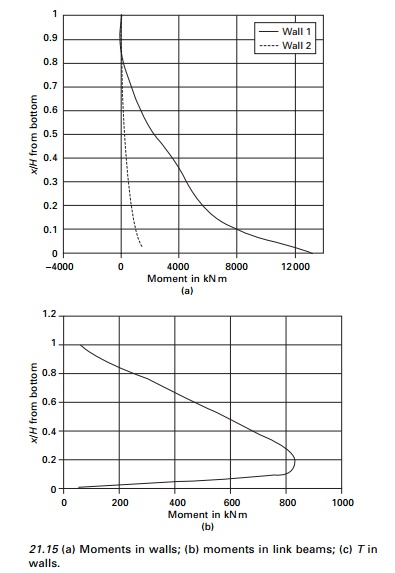
The calculations for the variations of moments, T, in the walls and the moment in the connecting beam are shown in Table 21.7 and the moments in both the walls, the moment in the link beam and T in the walls are shown in Fig. 21.15.

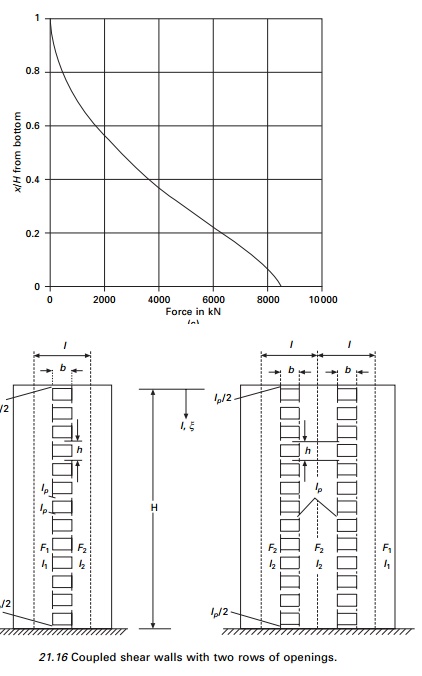
Coupled shear walls with two rows of openings are shown in Fig. 21.16.

Program 21.1 MATHEMATICA program for coupled shear wall

The program is executed in MATHEMATICA and the variation of moment in wall 1, moment in wall 2, moment in link beam and T of the wall are as shown in Fig. 20.15 for the coupled shear wall of height 73.15 m with width of the walls 4.88 and 2.44 m and thickness of the wall 0.3 m, width and depth of opening as 2.44 m, depth of link beam as 1.22 m and centre to centre of the wall as 6.1 m subjected to trapezoidal load of 30 k/m at the top and 15 kN/m at the bottom. Young’s modulus and Poisson’s ratio may be assumed as 20 GPa and 0.2 respectively. For the problem considered α² = 0.08237; ψ = 00114; c₂ = 15; c₃= –0.0346. The program in MATHEMATICA is shown on page 859.

DSolve[{T’’[x]-0.08237*T[x]==-0.0114*(15*x^2-0.0346*x^3),T[0]==T’[73.15]==0},T[x],x]

.

T=T[x]

t = –6.01903 ×  10^–7e^–0.287002x(8.37456 ×  10⁷

_{–8.37456 ×  10}7_e0.287002x  _{+ 1.e}0.574003x

–579519.e^0.287002xx²  + 7955.83e^0.287002xx³)

Plot[t,{x,0,73.15}] m=15*x^2-0.0346*x^3-t*6.1 m1=m*2.9557/3.2688 m2=m-m1 Plot[m1,{x,0,73.15}] Plot[m2,{x,0,73.15}] q=D[t,x] mlb=q*2.44*3.66/2 Plot[mlb,{x,0,73.15}]

Dsolve[{y”[x] == m/(20000000 * 3.2688), y[73.15] == y’[73.15] == 0}, y[x],x] z=y[x]

z =  6.81818 × 10⁻¹⁴ e^−0.287002x(8.37456 × 10 ⁷  + 3.38539

_×1011 _e 0.287002x _{x − 3.44906 × 10}6 _e 0.287002x _x3

_+4367.98e 0.287002x _x 4  _{− 6.04528e} 0.287002x _x4

−6.04525e ^0.287002x x⁵)

Plot[z,{x,0,73.15}]

Do[Print[“x,” “,t,” “,m1,” “, m1,” “,mlb,” “,z,” ], {x,0,73.15,7.315}]

If the same problem has to be carried out by finite element packages, the coupled shear wall has to be modelled into four-node finite elements. Wilson (2002) recommends that four-node element cannot model linear bending if fine mesh is used and produces infinite stresses. Hence the coupled shear wall has to be modelled into beam, column and rigid zones, otherwise the results are not reliable. Parametric studies for the coupled shear considered could be easily made by changing α, ψ in symbolic programming whereas it cannot be done so easily with the finite element method. 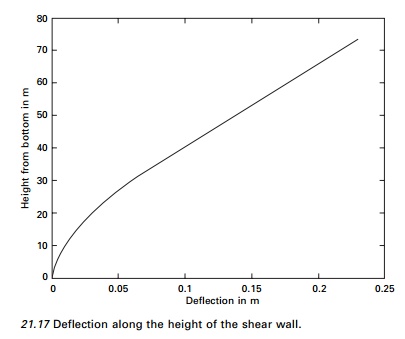The deflected shape of the shear wall is shown in Fig. 21.17.

Summary

In this chapter, analysis of shear wall with moment-resisting frame and coupled shear wall is discussed. Shear walls possess adequate lateral stiffness to reduce inter-storey distortions due to earthquake-induced motions. Shear walls reduce the likelihood of damage to non-structural elements of a building. When used with rigid frames, walls form a system that combines the gravity load-carrying efficiency of the rigid frames with the lateral load-resisting efficiency of the structural wall. Greater lateral stiffness is introduced in earthquake-resistant multi-storey shear wall buildings.