Approximate methods of analysis of multi-bay frames

Approximate methods of analysis of multi-bay frames (lateral loads)

1  Portal method (version 1)

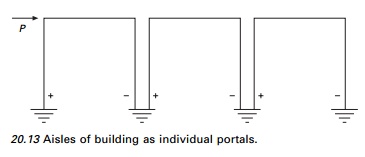
This method was developed by Robin Fleming (Norris and Wilbur,1960). The name is derived from the concept which treats aisles of buildings as individual portals, as shown in Fig. 20.13.

The load P is transmitted horizontally from portal, to portal giving rise to an independent overturning effect in all of them. The leeward and windward columns of each portal are subjected to compression and tension respectively. There is no direct stress in the interior columns. This method is the most expeditious of all the various methods of approximate analysis for wind and earthquake. In the absence of a marked design dissymmetry, this method is effective up to 25 stories.

The following assumptions are made (Version 1):

The points of contra-flexure are at the mid-points of the columns and girders.

The sum of all the earthquake loads above a given storey is distributed as shear among the columns of that storey, in direct proportion to the width of the aisles.

The bent resists all the earthquake load (with no help from the walls, floors and partition). This assumption is common to all the methods.

Steps

1.     Compute the wind or earthquake loads. In a typical panel, load is the storey height times the bay width times the unit wind or earthquake load. The roof load is based on half the height of the top storey plus the parapet wall if any.

2.     Distribute the wind or earthquake load as shear among its columns in direct proportion to the width of the aisles. In case of equal width aisles, the exterior columns of the bent are assumed to take half as much shear as interior ones.

3.     Compute the moments in all the columns. Since the points of contra-flexure are assumed to be at mid-storey height, the moments at the top and bottom will be equal to the product of column shear and half the storey height.

4.     Beginning at the upper left corner of the bent and work towards the right and downward.

5.     Find the shear in the girders. The shear in the girder is equal to its end moment divided by half of its span.

6.     Find the direct stress in the columns. This is done by taking out the joints one at a time as free bodies and apply ∑ V = 0.

7.     Find the direct stress in girders in the same free bodies used in step 6 and apply ∑ H = 0.

The free body diagram is shown in Fig. 20.14 and the bending moment diagram in Fig. 20.15.

2  Portal method version II

The assumptions are same as in Version I except that shear in interior columns is twice the shear is exterior columns whatever the aisle width. The free body

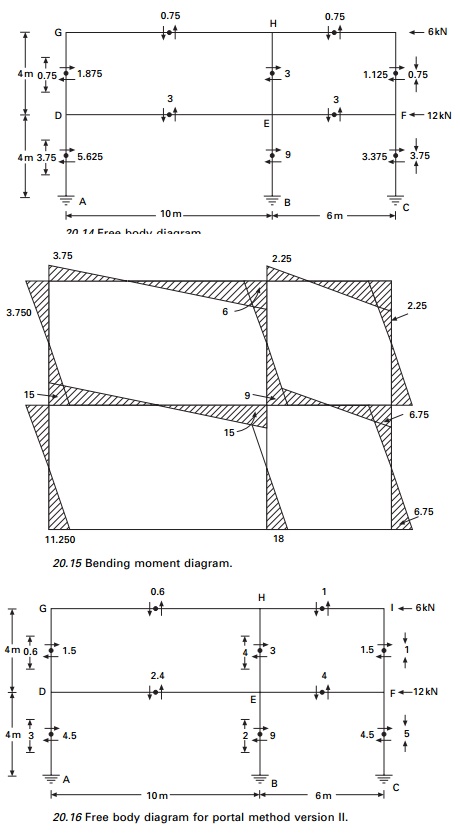
and bending moment diagrams (BMD) are shown in Figs 20.16 and 20.17 respectively.

3  Cantilever method – Robin Fleming (1913)

The building is treated as a cantilever beam standing on end and fixed to the ground. The beam formula thus applies and the columns become chord members under an increasing direct stress from the neutral axis of the building

outward. This method is effective up to about 35 stories provided the height to width ratio is not greater than four or five to one and provided the bents are not too much out of symmetry. It must be assumed that in order to get cantilever action, the interior girders must be sufficiently stiff to hold the floors in a plane under lateral deflection from wind. This calls for a comparatively low length–depth ratio for the girders when shallow girder– column an earthquake wind connection is used.

The following assumptions are made:

1.       The direct stress in a column is directly proportional to its distance from the neutral axis of the bent.

2.       The point of contra-flexure in the girders is at mid-span.      

3.       The points of contra-flexure of the columns are at mid-height.        

Steps it is usual to assume cross-sectional area of columns to be equal to 1:

1.     Locate the neutral axis of the bent by taking static moments of the column areas about either external column.

2.     Compute the moment of inertia of the column areas.

3.     Compute the external wind shears and moments to be applied at each mid-story height and record them.

4.     Compute direct stress in the exterior columns by f = My/I.

5.     Beginning at the upper left corner of the bent and working toward the 

right and downward, find and record girder shears. This is done by considering the free body and applying ∑ V = 0.

6.     Find and record girder moments. They are equal to the product of girder shear times half the span.

7.     Find and record column moments.

8.     Find and record beam moments.

The sum of the column shears across any storey should be equal to the total external shear taken by that story. The free body and bending moment diagrams are shown in Figs 20.18 and 20.19 respectively.

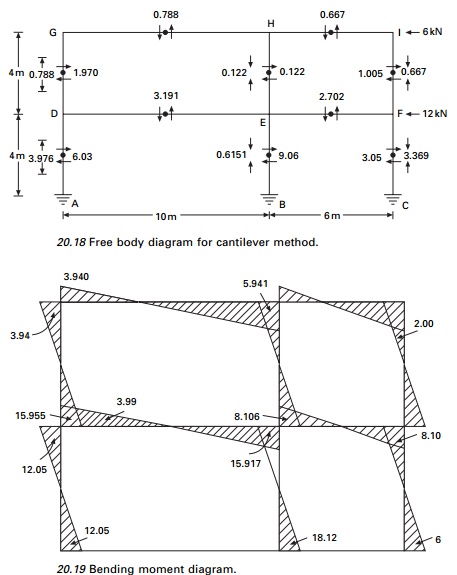
Taking the moment at A (see Fig. 20.18) we can find the neutral axis as

Top storey

Moment at mid-height of top storey = 6  2 = 12 kN m Taking the moment about the  neutral axis

k(1.33² + 7.34² + 8.67²) = 12; k = 0.091 Reaction in column GD = 0.091 × 8.67 = 0.788 Reaction in column HE = 1.34 × 8.67 = 0.122 Reaction in column IE = 7.34 × 8.67 = 0.667

Ground storey

Similarly taking moment at mid-height of bottom storey

k(1.33² + 7.34² + 8.67²) = 60; k = 0.4591 Reaction in DA = 0.451 × 8.67 = 3.976 Reaction in EB = 0.4591 × 1.34 = 0.6151 Reaction in CF = 0.4591 × 7.34 = 3.369

4  The factor method

The factor method (Wilbur, 1934) is another approximate method for analysing building frames subject to lateral loads. This method is said to be more accurate than either the portal or the cantilever method. In portal or cantilever methods, certain stress assumptions are made so as to make the structure determinate. In this method the same assumptions regarding the elastic action of the structure are made. These assumptions enable an approximate slope deflection analysis of the bent to be made.

In the previous methods, the relative K values of the members do not enter into the calculations, but this method takes the relative K-values of the members. To this extent, the results of this method are more accurate than other methods.

Steps:

For each joint, compute the girder factor ‘g’ by using g = ∑ K_c/∑ K (as shown in Table 20.2) where ∑ K_c = sum of k values of all columns meeting at the joint, ∑ K = sum of k values of all members meeting at the joints. Write ‘g’ values at the near end of each joint.

2.       For each joint, compute column factor ‘c’ as c = 1 – g; write c values at near end. For fixed column bases of first storey take c = 1.      

3.       To each of these members of c or g values add half of the number at the   other end of the members.       

4.       Multiply each sum from step 3, by the K values of the member concerned.        For columns, call this factor the column moment factor Cm; for girders call this factor the girder moment factor Gm.       

5.       The column moment factors obtained from step 4 are actually approximate      relative values for column end moments in that storey. The sum of the column end moments in a storey is equal by statics to the total horizontal shear of the storey multiplied by storey height. Hence individual column         moments may be found.

6.       Girder moment factors Gm from step 4 are really relative end moment     values for the girders at each joint. The sum of girder end moments at each joint is equal to sum of column end moments at that joint. Hence girder end moments can be worked out.

7.       Knowing the end moments of all members, other values such as girder     shears, column shears and column axial forces and girder forces can be worked out.       

The calculations are shown in Figs 20.20 and 20.21 and the bending moment diagram is shown in Fig. 20.22.

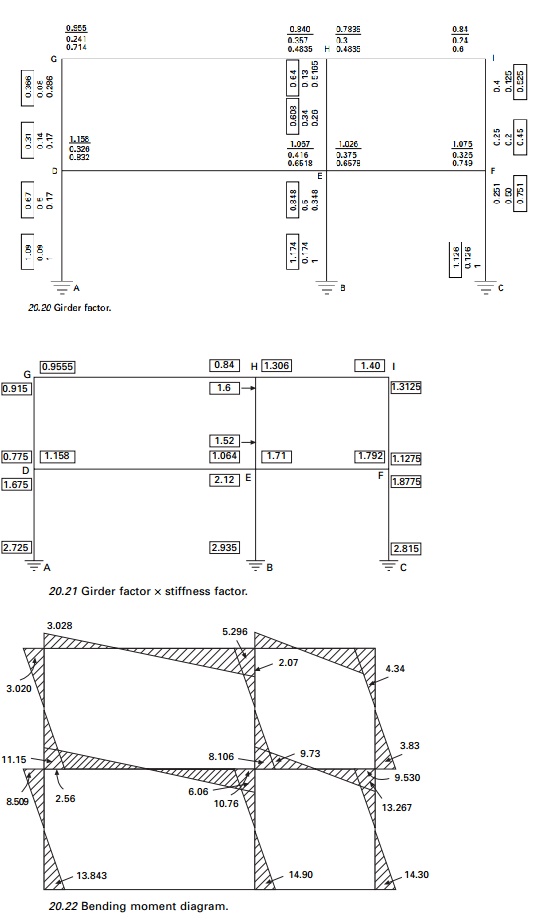
Assume stiffness of GH = I/10 = 1 

Corresponding stiffness of HI = 1 × 10/6 = 1.667 

Corresponding stiffness of DG = 1 × 10.4 = 2.5 

Corresponding stiffness of AD = 2.5

Multiply the factors obtained by stiffness factors; these values are given in Fig. 20.21.

Top storey column moments

A(0.915 + 0.775 + 1.6 + 1.52 + 1.3125 + 1.1275) = 24; A = 3.31

M_GD = 3.31 × 0.915 = 3.028

and similarly other moments are calculated and the moment diagram is shown in Fig. 20.22.

4  The factor method

5  Stiffness centre method

With the exception of the factor method, the portal and cantilever methods both assume that there is a point of inflexion at the mid-points of each girder and column when the building frame is subjected to lateral loads (Kardestuncer, 1974a).

In the cantilever method the magnitude of axial force in each column varies according to the distance of the centre of gravity of all columns under consideration. When a system consists of hollow portions or is made of beams and columns, due to rotations of girders the plane sections no longer remain plane after the application of loads. Hence the concept of centre of gravity in the cantilever method is a grossly wrong assumption, although the factor method formulated by Wilbur has improved the calculations considerably.

Steps:

1.                 Calculate axial stiffness coefficients

Quite often, since the change in length of a member has very little effect it can be omitted. The second term in this equation represents the summation of transverse bending stiffness of girders attached to the column. Note that the cantilever method omits the second term instead of the first (see Fig 20.23).        

2.  Locate the stiffness centre by 

3.  The axial force developed in each column due to total moment of all forces above the mid-height of the storey under consideration will be computed analogous to the axial stress distribution in a cross-section, but having the neutral axis located at the stiffness centre.

4.  Calculate transverse stiffness coefficients as

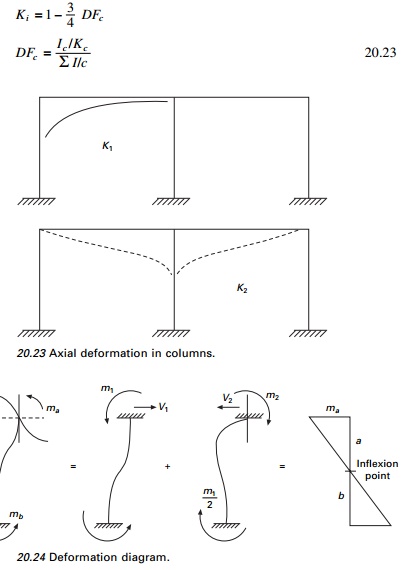
The deformation diagram is shown in Fig. 20.24.

5.  Distribute the wind shear according to the transverse stiffness coefficients

The above equation explains why the interior columns of a storey with equal size of columns carry larger transverse force than do the exterior columns. The ratio, however, is never twice.

6.  The inflexion point of a column may be located as

 For columns with a fixed base, the inflexion point is between the mid-height and the top of the column. Most often it is found to be located at 0.6L–0.7L from the base rather than 0.5L. The inflexion point is higher in exterior columns than in interior columns.

7.Calculate moments and shears. Axial stiffness coefficients

   8.Calculate stiffness centre

The inflexion point may be assumed to be between 0.6 and 0.7L from base. Knowing the shear, the column moment may be calculated. From the column moments beam moments may be calculated. The bending moment diagram by the stiffness centre method is shown in Fig. 20.25.

A comparison of various methods is given in Table 20.3.

Analysis of buildings simple in plan for lateral loads

The distribution of the load to the VLLR elements depends on the stiffness and rigidity of the diaphragm. If the diaphragm is rigid, the lateral force acting in a particular storey can be distributed to the VLLR elements in proportion to their stiffness.

The following assumptions are made:

1.     All the elements are connected by a rigid deck.

2.     The axes passes through centre of stiffness.

3.     Forces and distances are positive in the positive coordinate direction; rotations and moments are positive in the anticlockwise direction.

Let CS be the centre of stiffness. The displacement at centre of stiffness may be defined as (see Fig. 20.26)

Displacement of CS in x direction = U_C

Displacement of CS in y direction = V_C

Angle of rotation = θ

The centre of stiffness can be determined as follows. Consider the ith column (see Fig. 20.27)

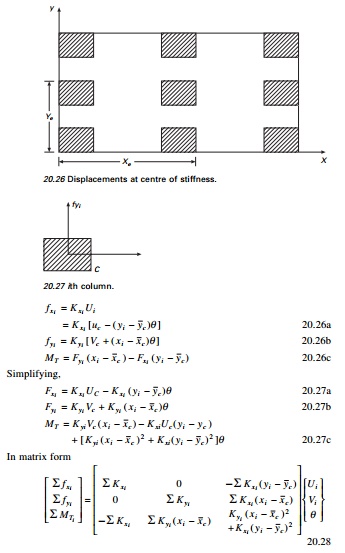
In the case of an unsymmetric plan of the building, the resultant eccentric to and acting at the centre of mass may be replaced by an equivalent load and a moment ‘M’ acting at the centre of the stiffness. The forces acting on each column may be denoted as in the x and y directions.