Definition, Solved Example Problems | Applied Statistics - Weighted Index Number | 12th Business Maths and Statistics : Chapter 9 : Applied Statistics
Chapter: 12th Business Maths and Statistics : Chapter 9 : Applied Statistics
Weighted Index Number
Weighted
Index Number
In general, all the
commodities cannot be given equal importance, so we can assign weights to each
commodity according to their importance and the index number computed from
these weights are called as weighted index number. The weights can be
production, consumption values. If ‘w’ is the weight attached to a commodity,
then the price index is given by,
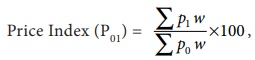
Let us consider the following notations,
p1 - current
year price
p0 - base year price
q1 - current
year quantity
q0 - base
year quantity
where suffix ‘0’
represents base year and ‘1’ represents current year.

Note
To get exact Fisher’s
price index number, one should use formula method rather than using
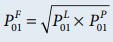
In Laspeyre’s price
index number, the quantity of the base year is used as weight.
In Paasche’s price
index number, the quantity of the current year is used as weight.
Example
9.10
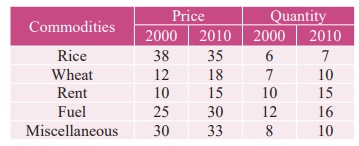
Calculate the
Laspeyre’s, Paasche’s and Fisher’s price index number for the following data.
Interpret on the data.
Solution

Laspeyre’s price index
number
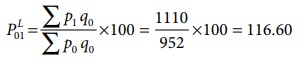
On an average, there is an increase
of 16.60 % in the price of the commodities when the year 2000 compared with the
year 2010.
Paasche’s price index number
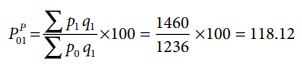
On an average, there is an increase
of 18.12 % in the price of the commodities when the year 2000 compared with the
year 2010.
Fisher’s price index number
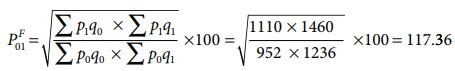
On an average, there is an increase
of 17.36 % in the price of the commodities when the year 2000 compared with the
year 2010.
Example
9.11
Construct the Laspeyre’s
, Paasche’s and Fisher’s price index number for the following data. Comment on
the result.
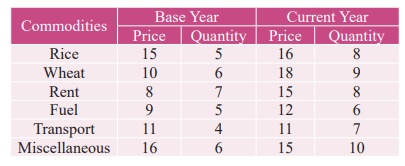
Solution
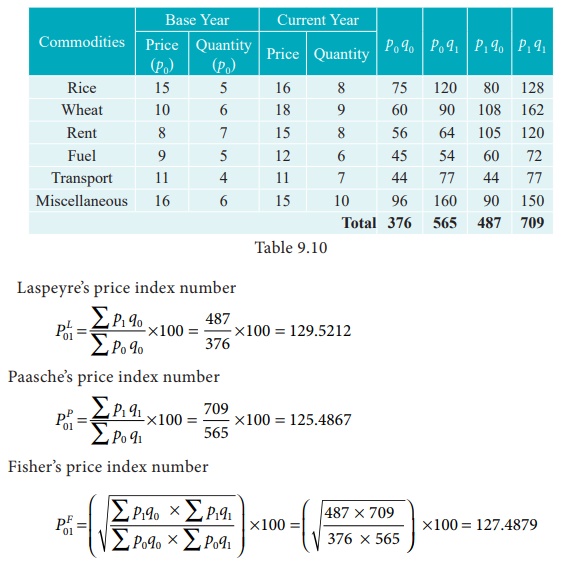
On an average, there is an increase of 29.52 % , 25.48% and 27.48% in the price of the commodities by Laspeyre’s, Paasche’s, Fisher’s price index number respectively, when the base year compared with the current year.
Related Topics