Test of adequacy for an Index Number

Test of adequacy for an Index Number

Index numbers are studied to know the relative changes in price and quantity for any two years compared. There are two tests which are used to test the adequacy for an index number. The two tests are as follows,

(i) Time Reversal Test

(ii) Factor Reversal Test

The criterion for a good index number is to satisfy the above two tests.

Time Reversal Test

It is an important test for testing the consistency of a good index number. This test maintains time consistency by working both forward and backward with respect to time (here time refers to base year and current year). Symbolically the following relationship should be satisfied, P₀₁ × P₁₀ =1

Fisher’s index number formula satisfies the above relationship

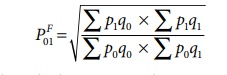
when the base year and current year are interchanged, we get

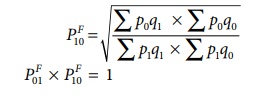
Factor Reversal Test

This is another test for testing the consistency of a good index number. The product of price index number and quantity index number from the base year to the current year should be equal to the true value ratio. That is, the ratio between the total value of current period and total value of the base period is known as true value ratio. Factor Reversal Test is given by,

Example 9.12

Calculate Fisher’s price index number and show that it satisfies both Time Reversal Test and Factor Reversal Test for data given below.

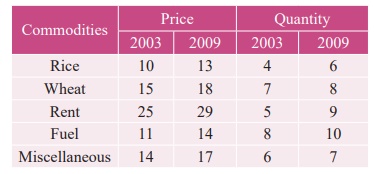
Solution

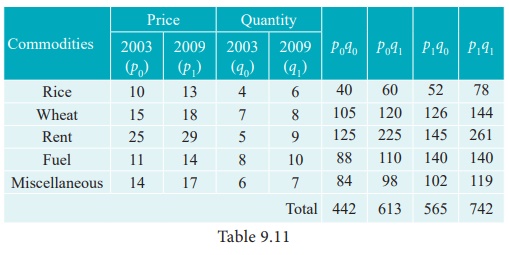
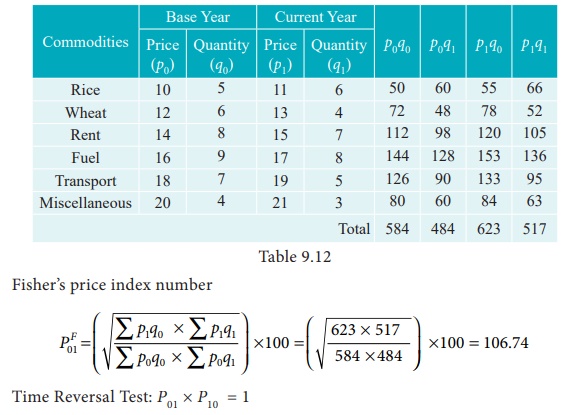
Example 9.13

Calculate Fisher’s price index number and show that it satisfies both Time Reversal Test and Factor Reversal Test for data given below.

Solution

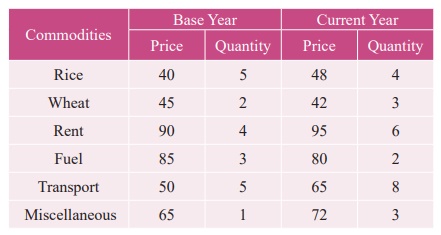
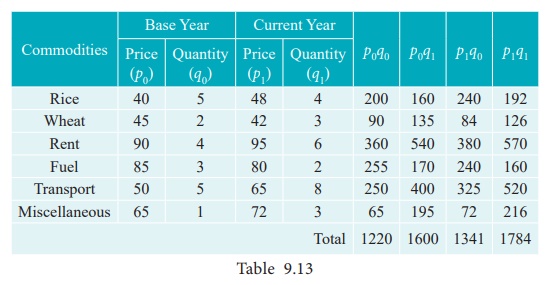
Example 9.14

Construct Fisher’s price index number and prove that it satisfies both Time Reversal Test and Factor Reversal Test for data following data.

Solution