Wave Nature of Light

WAVE NATURE OF LIGHT

Light is a transverse, electromagnetic wave. The wave nature of light was first illustrated through experiments on interference and diffraction. Like all electromagnetic waves, light can travel through vacuum. The transverse nature of light is demonstrated in polarization.

1. Wave optics

Wave optics deals with the wave characteristics of light. With the help of wave optics, we are going to learn in details the phenomena of interference, diffraction and polarization. Even the law of reflection and refraction are proved only with the help of wave optics. Though light propagates as a wave, its direction of propagation is still represented as a ray.

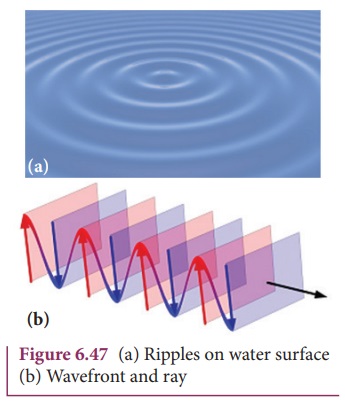
An example for wave propagation is the spreading of circular ripples on the surface of still water from a point at which a stone is dropped. The molecules or particles of water are moving only up and down (oscillate) when a ripple passes out that part. All these particles on the circular ripple are in the same phase of vibration as they are all at the same distance from the center. The ripple represents a wavefront as shown in Figure 6.47(a). A wavefront is the locus of points which are in the same state or phase of vibration. When a wave propagates it is treated as the propagation of wavefront. The wavefront is always perpendicular to the direction of the propagation of the wave. As the direction of ray is in the direction of propagation of the wave, the wavefront is always perpendicular to the ray as shown in Figure 6.47(b).

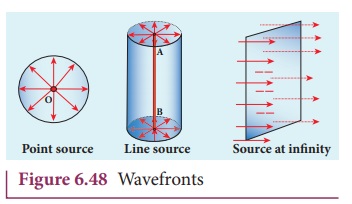
The shape of a wavefront observed at a point depends on the shape of the source and also the distance at which the source is located. A point source located at a finite distance gives spherical wavefronts. An extended (or) line source at finite distance gives cylindrical wavefronts. The plane wavefronts are received from any source that is located at infinity as shown in Figure 6.48.

2. Huygens’ Principle

Huygens principle is a geometrical construction which gives the shape of the wavefront at any time if we know its shape at t = 0. According to Huygens principle, each point of the wavefront is the source of secondary wavelets emanating from these points spreading out in all directions with the speed of the wave. These are called as secondary wavelets. The common tangent, in other words the envelope to all these wavelets gives the position and shape of the new wavefront at a later time. Thus, Huygens’ principle explains the propagation of a wavefront.

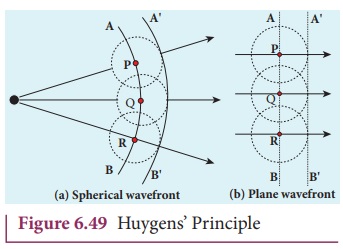
The propagation of a spherical and plane wavefront is explained in using Huygens’ principle. Let, AB be the wavefront at a time, t = 0. According to Huygens’ principle, every point on AB acts as a source of secondary wavelet which travels with the speed of the wave (speed of light c). To find the position of the wavefront after a time t, circles of radius equal to ct are drawn with points P, Q, R ... etc., as centers on AB. The tangent or forward envelope A’ B’ of the small circles is the new wavefront at that instant.

The wavefront A’ B’ will be a spherical wavefront from a point object which is at a finite distance as shown in Figure 49(a) and it is a plane wavefront if the source of light is at a large distance (infinity) as shown in Figure 6.49(b).

There is one shortcoming in the above Huygens’ construction for propagation of a wavefront. It could not explain the absence of backwave which also arises in the above construction. According to electromagnetic wave theory, the backwave is ruled out inherently. However, Huygens’ construction diagrammatically explains the propagation of the wavefront.

3. Proof for laws of reflection using Huygens’ Principle

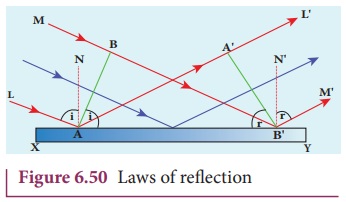
Let us consider a parallel beam of light, incident on a reflecting plane surface such as a plane mirror XY as shown in Figure 6.50. The incident wavefront is AB and the reflected wavefront is A’ B’ in the same medium. These wavefronts are perpendicular to the incident rays L, M and reflected rays L’ , M ‘ respectively. By the time point A of the incident wavefront touches the reflecting surface, the point B is yet to travel a distance BB’ to touch the reflecting surface at B’ . When the point B falls on the reflecting surface at B’ , the point A would have reached A’ .

This is applicable to all the points on the wavefront. Thus, the reflected wavefront A’ B’ emanates as a plane wavefront. The two normals N and N ‘ are considered at the points where the rays L and M fall on the reflecting surface. As reflection happens in the same medium, the speed of light is same before and after the reflection. Hence, the time taken for the ray to travel from B to B’ is the same as the time taken for the ray to travel from A to A’ . Thus, the distance BB’ is equal to the distance AA’ ; (AA’ = BB’) .

(i) The incident rays, the reflected rays and the normal are in the same plane.

(ii) Angle of incidence,

∠i = ∠NAL = 90º – ∠NAB = ∠ BAB’

Angle of reflection,

∠r = ∠ N ‘ B’M ‘ = 90º –∠N ‘ B’A’ = ∠ A’B’A

For the two right angle triangles, ∆ ABB’ and ∆ B’A’A , the right angles, ∠B and ∠ A’ are equal, (∠B and ∠ A’ = 90º); the two sides, AA’ and BB’ are equal, (AA’ = BB’); the side AB’ is the common. Thus, the two triangles are congruent. As per the property of congruency, the two angles, ∠ BAB’ and ∠ A’ B’A must also be equal.

 i= r          (6.1)

Hence, the laws of reflection are proved.

4. Proof for laws of refraction using Huygens’ Principle

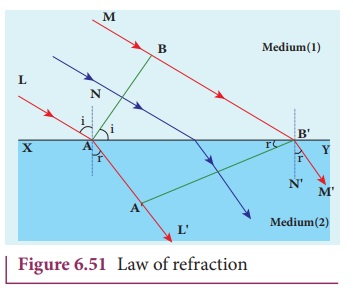
Let us consider a parallel beam of light is incident on a refracting plane surface XY such as a glass surface as shown in Figure 6.51. The incident wavefront AB is in rarer medium (1) and the refracted wavefront A’ B’ is in denser medium (2) These wavefronts are perpendicular to the incident rays L, M and refracted rays L’,M ‘ respectively. By the time the point A of the incident wavefront touches the refracting surface, the point B is yet to travel a distance BB’ to touch the refracting surface at B’.

When the point B falls on the refracting surface at B’, the point A would have reached A’ in the other medium. This is applicable to all the points on the wavefront. Thus, the refracted wavefront A’ B’ emanates as a plane wavefront. The two normals N and N ‘ are considered at the points where the rays L and M fall on the refracting surface. As refraction happens from rarer medium (1) to denser medium (2), the speed of light is v₁ and v₂ before and after refraction and v₁ is greater than v₂ (v₁>v₂). But, the time taken t for the ray to travel from B to B’ is the same as the time taken for the ray to travel from A to A’ .

(i) The incident rays, the refracted rays and the normal are in the same plane.

(ii) Angle of incidence,

 i = ∠NAL = 90º – ∠NAB = ∠ BAB’

Angle of refraction,

 r = ∠ N ‘B’M ‘ = 90º – ∠ N ‘B’A’ = ∠A’B’A

For the two right angle triangles ∆ ABB’ and ∆ B’A’A ,

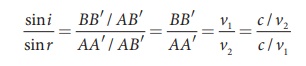
Here, c is speed of light in vacuum. The ratio c/v is the constant, called refractive index of the medium. The refractive index of medium (1) is, c/v₁ = n₁ and that of medium (2) is, c/v₂ = n₂.

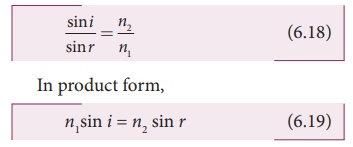
Hence, the laws of refraction are proved.

In the same way the laws of refraction can also be proved for wavefront travelling from denser to rarer medium.

Light travels with greater speed in rarer medium and lesser speed in denser medium Hence, the wavelength of the light is longer in rarer medium and shorter in denser medium.

If light of a particular frequency travels through different media, then, its frequency remains unchanged in all the media. Only the wavelength changes according to speed of light in that medium.

EXAMPLE 6.23

The wavelength of light from sodium source in vacuum is 5893Ã….What are its (a) wavelength, (b) speed and (c) frequency when this light travels in water which has a refractive index of 1.33.

Solution

The refractive index of vacuum, n₁ = 1

The wavelength in vacuum, λ₁ = 5893 Ã….

The speed in vacuum, c = 3 × 10⁸ m s^–1

The refractive index of water, n₂ = 1.33

The wavelength of light in water, λ₂

The speed of light in water, v₂

(a) The equation relating the wavelength and refractive index is,

(b) The equation relating the speed and refractive index is,

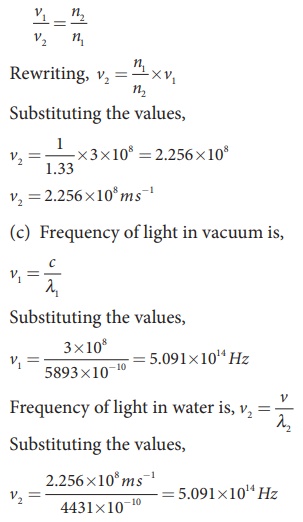
The results show that the frequency remains same in all media.