Interference

INTERFERENCE

The phenomenon of addition or superposition of two light waves which produces increase in intensity at some points and decrease in intensity at some other points is called interference of light.

Superposition of waves refers to addition of waves. The concept of superposition of mechanical waves is studied in (XI Physics 11.7). When two waves simultaneously pass through a particle in a medium, the resultant displacement of that particle is the vector addition of the displacements due to the individual waves. The resultant displacement will be maximum or minimum depending upon the phase difference between the two superimposing waves. These concepts hold good for light as well.

Let us consider two light waves from the two sources S₁ and S₂ meeting at a point P as shown in Figure 6.52.

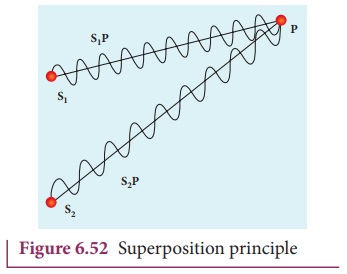
The wave from S₁ at an instant t at P is,

The two waves have different amplitudes a₁ and a₂, same angular frequency ω, and a phase difference of ϕ between them. The resultant displacement will be given by,

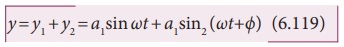
The simplification of the above equation by using trigonometric identities as done in (XI Physics 11.7) gives the equation,

The resultant amplitude is minimum,

The intensity of light is proportional to square of amplitude,

In equation 6.126 if the phase difference, ϕ = 0, ±2π, ±4π. . . , it corresponds to the condition for maximum intensity of light called as constructive interference.

The resultant maximum intensity is,

In equation 6.126 if the phase difference, ϕ = ±π, ±3π, ±5π. . . , it corresponds to the condition for minimum intensity of light called destructive interference.

The resultant minimum intensity is,

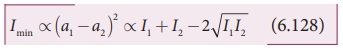
As a special case, if a₁ = a₂ = a, then equation 6.121. becomes,

We conclude that the phase difference ϕ, between the two waves decides the intensity of light at that point where the two waves meet.

EXAMPLE 6.24

Two light sources with amplitudes 5 units and 3 units respectively interfere with each other. Calculate the ratio of maximum and minimum intensities.

Solution

Amplitudes, a₁ = 5, a₂ = 3

Resultant amplitude,

EXAMPLE 6.25

Two light sources of equal amplitudes interfere with each other. Calculate the ratio of maximum and minimum intensities.

Solution

Let the amplitude be a.

The intensity is, I ∝ µ 4a² cos²(ϕ/ 2)

or I = 4I₀ cos²(ϕ/2)

Resultant intensity is maximum when,

 ϕ  = 0, cos0 = 1, I_max ∝ 4a²

Resultant amplitude is minimum when,

 ϕ = π, cos(π/2) = 0, I_min = 0

I_max : I_min = 4a² : 0

EXAMPLE 6.26

Two light sources have intensity of light as I₀. What is the resultant intensity at a point where the two light waves have a phase difference of π/3?

Solution

Let the intensities be I₀.

The resultant intensity is, I = 4I₀cos²(ϕ/2)

Resultant intensity when, ϕ = π / 3, is

 I = 4I₀ cos² (π/6)

  I = 4I_o (√3/2)² = 3I_o

1. Phase difference and path difference

Phase is the angular position of a vibration. As a wave is progressing, there is a relation between the phase of the vibration and the path travelled by the wave. One can express the phase in terms of path and vice versa. In the path of the wave, one wavelength λ corresponds to a phase of 2π as shown in Figure 6.53. A path difference δ corresponds to a phase difference ϕ as given by the equation,

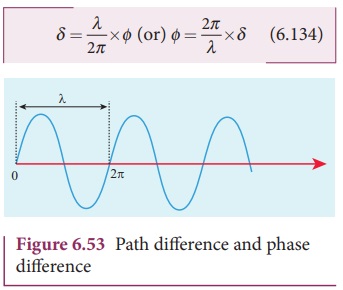
For constructive interference, the phase difference should be, ϕ = 0, 2π, 4π . . . Hence, the path difference must be, δ = 0, λ, 2λ . . . In general, the integral multiples of λ.

For destructive interference, phase difference should be, ϕ = π, 3π, 5π . . . Hence, the path difference must be, δ = λ/2 , 3λ/2 .....

In general, the half integral multiples of λ.

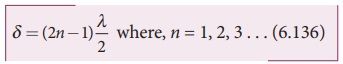
EXAMPLE 6.27

The wavelength of a light is 450 nm. How much phase it will differ for a path of 3 mm?

Solution

The wavelength is, λ = 450 nm = 450×10^-9m

Path difference is, δ = 3 mm = 3×10⁻³m

Relation between phase difference and path difference is, ϕ = 2π/λ ×δ

Substituting,

 ϕ = [ 2π / 450×10^-9 ] ×3×10⁻³ = (π/75) ×10⁶

 ϕ = (π/75) ×10⁶ rad

2. Coherent sources

Two light sources are said to be coherent if they produce waves which have same phase or constant phase difference, same frequency or wavelength (monochromatic), same waveform and preferably same amplitude. Coherence is a property of waves that enables to obtain stationary interference patterns.

Two independent monochromatic sources can never be coherent, because they may emit waves of same frequency and same amplitude, but not with same phase. This is because, atoms while emitting light, produce change in phase due to thermal vibrations. Hence, these sources are said to be incoherent sources.

To obtain coherent light waves, we have three techniques. They are,

(i) Intensity or amplitude division

(ii) wavefront division

(iii) source and images.

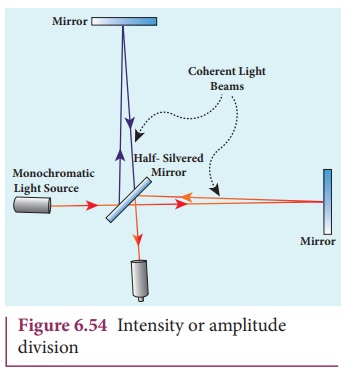
(i) Intensity or amplitude division: If we allow light to pass through a partially silvered mirror (beam splitter), both reflection and refraction take place simultaneously. As the two light beams are obtained from the same light source, the two divided light beams will be coherent beams. They will be either in-phase or at constant phase difference as shown in Figure 6.54. Instruments like Michelson’s interferometer, Fabray-Perrot etalon work on this principle.

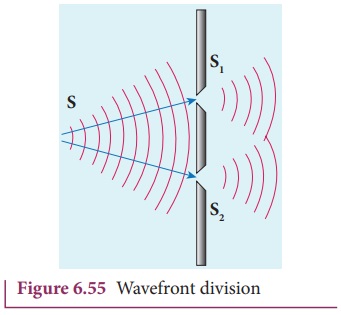
(ii) Wavefront division: This is the most commonly used method for producing two coherent sources. We know a point source produces spherical wavefronts. All the points on the wavefront are at the same phase. If two points are chosen on the wavefront by using a double slit, the two points will act as coherent sources as shown in Figure 6.55.

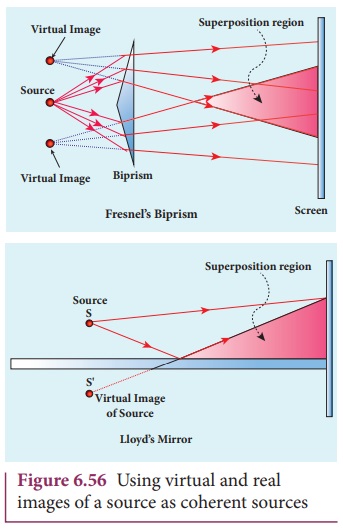
(iii) Source and images: In this method a source and its image will act as a set of coherent source, because the source and its image will have waves in-phase or constant phase difference as shown in Figure 6.56. The Instrument, Fresnel’s biprism uses two virtual sources as two coherent sources and the instrument, Lloyd’s mirror uses a source and its virtual image as two coherent sources.

3. Double slit as coherent sources

Double slit uses the principle of wavefront division. Two slits S₁ and S₂ illuminated by a single monochromatic source S act as a set of coherent sources. The waves from these two coherent sources travel in the same medium and superpose. The constructive and destructive interference are shown in Figure 6.57(a).The crests of the waves are shown by thick continuous lines and troughs are shown by broken lines in Figure 6.57(b).

At points where the crest of one wave meets the crest of the other wave or the trough of one wave meets the trough of the other wave, the waves are in-phase. Hence, the displacement is maximum and these points appear bright. This type of interference is said to be constructive interference.

At points where the crest of one wave meets the trough of the other wave and vice versa, the waves are out-of-phase. Hence, the displacement is minimum and these points appear dark. This type of interference is said to be destructive interference.

On a screen the intensity of light will be alternatively maximum and minimum i.e. bright and dark bands which are referred as interference fringes.

4. Young’s double slit experiment

Thomas Young, a British Physicist used an opaque screen with two small openings called double slit S₁ and S₂ kept equidistance from a source S as shown in Figure 6.62. The width of each slit is about 0.03 mm and they are separated by a distance of about 0.3 mm. As S₁ and S₂ are equidistant from S, the light waves from S reach S₁ and S₂ in-phase. So, S₁ and S₂ act as coherent sources which are the requirement of obtaining interference pattern.

Experimental setup

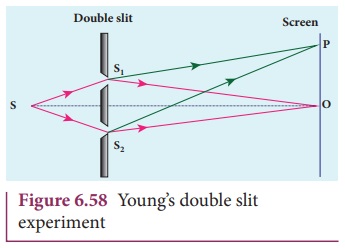
Wavefronts from S₁ and S₂ spread out and overlapping takes place to the right side of double slit. When a screen is placed at a distance of about 1 meter from the slits, alternate bright and dark fringes which are equally spaced appear on the screen. These are called interference fringes or bands. Using an eyepiece the fringes can be seen directly. At the center point O on the screen, waves from S₁ and S₂ travel equal distances and arrive in-phase as shown in Figure 6.58. These two waves constructively interfere and bright fringe is observed at O. This is called central bright fringe. The fringes disappear and there is uniform illumination on the screen when one of the slits is covered. This shows clearly that the bands are due to interference.

Equation for path difference

The schematic diagram of the experimental set up is shown in Figure 6.59. The Let d be the distance between the double slits S₁ and S₂ which act as coherent sources of wavelength λ. A screen is placed parallel to the double slit at a distance D from it. The mid-point of S₁ and S₂ is C and the mid-point of the screen O is equidistant from S₁ and S₂. P is any point at a distance y from O. The waves from S₁ and S₂ meet at P either in-phase or out-of-phase depending upon the path difference between the two waves.

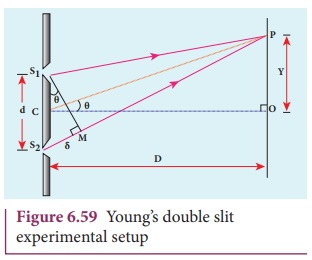
The path difference δ between the light waves from S₁ and S₂ to the point P is, δ = S₂P – S₁P

A perpendicular is dropped from the point S₁ to the line S₂P at M to find the path difference more precisely.

 δ = S₂P – MP = S₂M                          …….(6.137)

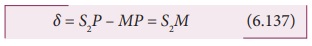
The angular position of the point P from C is θ. ∠OCP = θ.

From the geometry, the angles ∠OCP and ∠S₂S₁M are equal.

∠OCP = ∠S₂S₁M = θ.

In right angle triangle ∆S₁S₂M, the path difference, S₂M = d sin θ

If the angle θ is small, sin θ ≈ tan θ ≈ θ

From the right angle triangle ∆OCP, tanθ = y/D

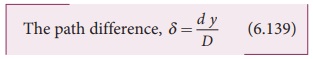
Based on the condition on the path difference, the point P may have a bright or dark fringe.

Condition for bright fringe (or) maxima

The condition for the constructive interference or the point P to be have a bright fringe is,

Path difference, δ = nλ

where, n = 0, 1, 2, . . .

 ∴ d y/D = nλ

This is the condition for the point P to be a bright fringe. The distance is the distance of the nth bright fringe from the point O.

Condition for dark fringe (or) minima

The condition for the destructive interference or the point P to be have a dark fringe is,

Path difference, δ = (2n −1) λ/2

where, n = 1, 2, 3 . . .

∴ d y/D = (2n −1) λ/2

This is the condition for the point P to be a dark fringe. The distance y_n is the distance of the n^th dark fringe from the point O.

The formation of bright and dark fringes is shown in Figure 6.60.

This shows that on the screen, alternate bright and dark bands are seen on either side of the central bright fringe. The central bright is referred as 0^th bright followed by 1st dark and 1st bright and then 2nd dark and 2nd bright and so on, on either side of O successively as shown in Figure 6.61.

Equation for bandwidth

The bandwidth (β) is defined as the distance between any two consecutive bright or dark fringes.

The distance between (n+1)^th and nth consecutive bright fringes from O is given by,

Similarly, the distance between (n+1)^th and n consecutive dark fringes from O is given by,

Equations (6.142) show that the bright and dark fringes are of same width equally spaced on either side of central bright fringe.

Conditions for obtaining clear and broad interference bands

(i) The screen should be as far away from the source as possible.

(ii) The wavelength of light used must be larger.

(iii) The two coherent sources (here S₁ and S₂) must be as close as possible.

EXAMPLE 6.28

In Young’s double slit experiment, the two slits are 0.15 mm apart. The light source has a wavelength of 450 nm. The screen is 2 m away from the slits.

(i) Find the distance of the second bright fringe and also third dark fringe from the central maximum.

(ii) Find the fringe width.

(iii) How will the fringe pattern change if the screen is moved away from the slits?

(iv) What will happen to the fringe width if the whole setup is immersed in water of refractive index 4/3.

Solution

d = 0.15 mm = 0.15× 10^-3 m; D = 2 m;

λ = 450 nm = 450 × 10^-9 m; n = 4/3

(i) Equation for nth bright fringe is,

(ii) Equation for fringe width is, 

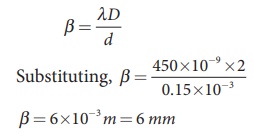
(iii) The fringe width will increase as D is increased,

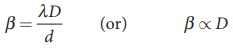
(iv) The fringe width will decrease as the setup is immersed in water of refractive index 4/3

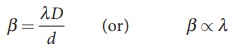
The wavelength will decrease refractive index n times.

Hence, β ∝ λ and β’ ∝ λ’

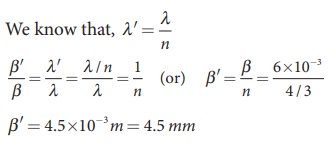
5. Interference with polychromatic light

When a polychromatic light (white light) is used in interference experiment, coloured fringes of varied thickness will be formed on the screen. This is because, different colours have different wavelengths. However, the central fringe or 0^th fringe will always be bright and white in colour, because for all the colours falling at the point O will have no path difference. Hence, only constructive interference is possible at O for all the colours.

EXAMPLE 6.29

Two lights of wavelengths 560 nm and 420 nm are used in Young’s double slit experiment. Find the least distance from the central fringe where the bright fringe of the two wavelengths coincides. Given D = 1 m and d = 3 mm.

Solution

λ = 560 nm = 560×10⁻⁹ m;

λ₂ = 420 nm = 420×10⁻⁹ m;

D = 1 m;d = 3 mm = 3×10⁻³ m

For a given y, n and λ are inversely proportional.

Let nth order bright fringe of λ₁ coincides with (n+1)^th order bright fringe of λ₂.

Thus, the 3rd bright fringe of λ₁ and 4th bright fringe of λ₂ coincide at the least distance y.

The least distance from the central fringe where the bright fringes of the two wavelengths coincides is, y_n = n [(λD)/d]

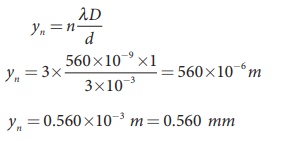
Dazzling colours are exhibited by thin films of oil spread on the surface of water and also by soap bubbles as shown in the figure. These colours are due to interference of white light undergoing multiple reflections from the top and the bottom surfaces of thin films. The colour depends upon the thickness of the film, refractive index of the film and also the angle of incidence of the light.

6. Interference in thin films

Let us consider a thin film of transparent material of refractive index µ (not to confuse with order of fringe n) and thickness d. A parallel beam of light is incident on the film at an angle i as shown in Figure 6.62. The wave is divided into two parts at the upper surface, one is reflected and the other is refracted. The refracted part, which enters into the film, again gets divided at the lower surface into two parts; one is transmitted out of the film and the other is reflected back in to the film. Reflected as well as refracted waves are sent by the film as multiple reflections take place inside the film. The interference is produced by both the reflected and transmitted light.

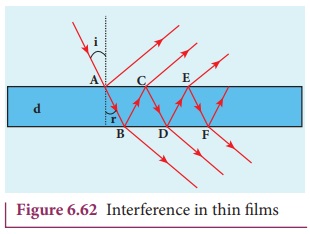
For transmitted light

The light transmitted may interfere to produce a resultant intensity. Let us consider the path difference between the two light waves transmitted from B and D. The two waves moved together and remained in phase up to B where splitting occurred. The extra path travelled by the wave transmitted from D is the path inside the film, BC + CD. If we approximate the incidence to be nearly normal (i = 0), then the points B and D are very close to each other. The extra distance travelled by the wave is approximately twice thickness of the film, BC + CD = 2d. As this extra path is traversed in a medium of refractive index µ, the optical path difference is, δ = 2µd.

The condition for constructive interference in transmitted ray is,

Similarly, the condition for destructive interference in transmitted ray is,

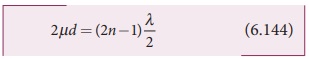
For reflected light

It is experimentally and theoretically proved that a wave while travelling in a rarer medium and getting reflected by a denser medium, undergoes a phase change of π. Hence, an additional path difference of λ/2 should be considered.

Let us consider the path difference between the light waves reflected by the upper surface at A and the other wave coming out at C after passing through the film. The additional path travelled by wave coming out from C is the path inside the film, AB + BC. For nearly normal incidence this distance could be approximated as, AB + BC = 2d. As this extra path is travelled in the medium of refractive index µ, the optical path difference is, δ = 2µd.

The condition for constructive interference for reflected ray is,

The additional path difference λ/2 is due to the phase change of π in rarer to denser reflection taking place at A.

The condition for destructive interference for reflected ray is,

If the incidence is not nearly normal, but at an angle of incidence i which has an angle of refraction r, then the expression for path difference 2µd on the left hand side of the above equations are to be replaced with the expression, 2µd cos r.

EXAMPLE 6.30

Find the minimum thickness of a film of refractive index 1.25, which will strongly reflect the light of wavelength 589 nm. Also find the minimum thickness of the film to be anti-reflecting.

Solution

λ = 589 nm = 589×10⁻⁹ m

For the film to have strong reflection, the reflected waves should interfere constructively. The least optical path difference introduced by the film should be λ/2. The optical path difference between the waves reflected from the two surfaces of the film is 2µd. Thus, for strong reflection, 2µd = λ/2 [As given in equation 6.145. with n = 1]

Rewriting, d = λ/4μ

Substituting, d = [589×10⁹] / [4×1.25] = 117.8×10⁻⁹

d = 117.8×10⁻⁹ = 117.8 nm

For the film to be anti-reflecting, the reflected rays should interfere destructively. The least optical path difference introduced by the film should be λ. The optical path difference between the waves reflected from the two surfaces of the film is 2µd. For strong reflection, 2µd = λ [As given in equation 6.146. with n = 1].

Rewriting, d = λ/2μ

Substituting, d = [589×10⁹] / [2×1.25] = 235.6×10⁻⁹

d = 235.6×10⁻⁹ = 235.6 nm