Diffraction

DIFFRACTION

Diffraction is a general characteristic of all types of waves, be it sound wave, light wave, water wave etc. Diffraction is bending of waves around sharp edges into the geometrically shadowed region. This is a violation to the rectilinear propagation of light, we have studied in ray optics, which says light should travel in straight line in a medium without bending. But, the diffraction is prominent only when the size of the obstacle is comparable to the wavelength of light. This is the reason why sound waves get diffracted prominently by obstacles like doors, windows, buildings etc. The wavelength of sound wave is large and comparable to the geometry of these obstacles. But the diffraction in light is more pronounced when the obstacle size is of the order of wavelength of light.

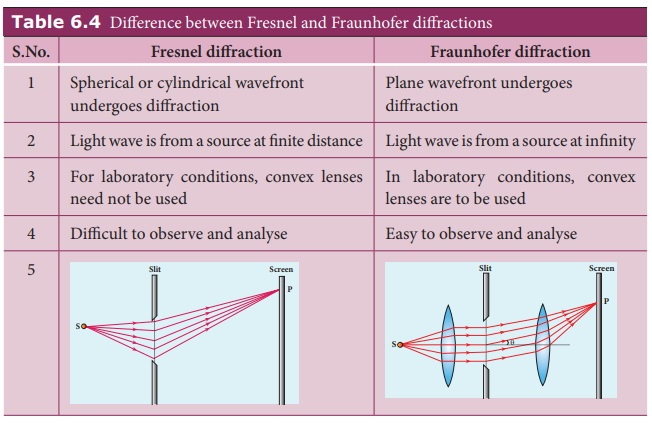
1. Fresnel and Fraunhofer diffractions

Based on the type of wavefront which undergoes diffraction, the diffraction could be classified as Fresnel and Fraunhofer diffractions. The differences between Fresnel and Fraunhofer diffractions are shown in Table 6.4.

As Fraunhofer diffraction is easy to observe and analyse, let us take it up for further discussions.

Table 6.4 Difference between Fresnel and Fraunhofer diffractions

Fresnel diffraction

• Spherical or cylindrical wavefront undergoes diffraction

• Light wave is from a source at finite distance

• For laboratory conditions, convex lenses need not be used

• Difficult to observe and analyse

Fraunhofer diffraction

• Plane wavefront undergoes diffraction

• Light wave is from a source at infinity

• In laboratory conditions, convex lenses are to be used

• Easy to observe and analyse

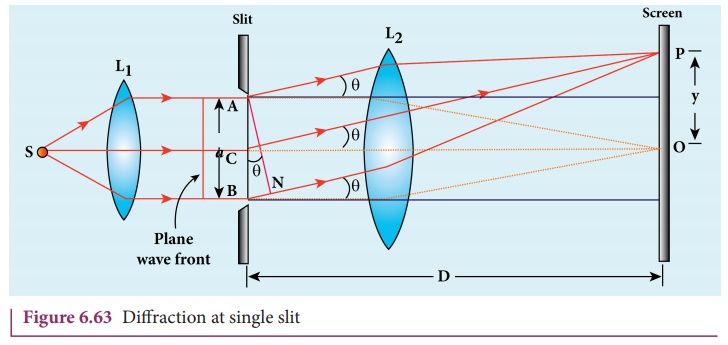
2. Diffraction at single slit

Let a parallel beam of light fall normally on a single slit AB of width a as shown in Figure 6.63. The diffracted beam falls on a screen kept at a distance. The center of the slit is C. A straight line through C perpendicular to the plane of slit meets the center of the screen at O. We would like to find the intensity at any point P on the screen. The lines joining P to the different points on the slit can be treated as parallel lines, making an angle θ with the normal CO.

All the waves start parallel to each other from different points of the slit and interfere at point P and other points to give the resultant intensities. The point P is in the geometrically shadowed region, up to which the central maximum is spread due to diffraction as shown Figure 6.63. We need to give the condition for the point P to be of various minima.

The basic idea is to divide the slit into much smaller even number of parts. Then, add their contributions at P with the proper path difference to show that destructive interference takes place at that point to make it minimum. To explain maximum, the slit is divided into odd number of parts.

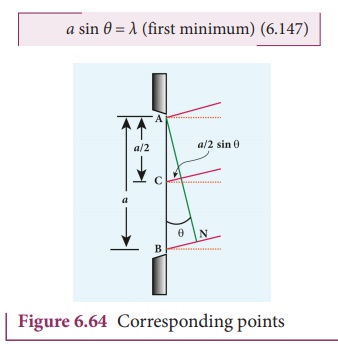
Condition for P to be first minimum

Let us divide the slit AB into two half ’s AC and CB. Now the width of AC is (a/2). We have different points on the slit which are separated by the same width (here a/2) called corresponding points as shown in Figure 6.64.

The path difference of light waves from different corresponding points meeting at point P and interfere destructively to make it first minimum. The path difference δ between waves from these corresponding points is, δ = a/2 sinθ

The condition for P to be first minimum, a/2 sinθ = λ/2

Condition for P to be second minimum

Let us divide the slit AB into four equal parts. Now, the width of each part is a/4. We have several corresponding points on the slit which are separated by the same width a/4. The path difference δ between waves from these corresponding points is, δ = a/4 sinθ.

The condition for P to be second minimum, a/4 sinθ = λ/2

a sin θ = 2λ (second minimum)                  (6.148)

Condition for P to be third order minimum

The same way the slit is divided in to six equal parts to explain the condition for P to be third minimum is, a/6 sinθ = λ/2

a sin θ = 3λ (third minimum) (6.149)

Condition for P to be nthorder minimum

Dividing the slit into 2n number of (even number of) equal parts makes the light produced by one of the corresponding points to be cancelled by its counterpart. Thus, the condition for nth order minimum is a/2n sinθ = λ/2

a sin θ = nλ (n^th minimum)       (6.150)

Condition for maxima

For points of maxima, the slit is to be divided in to odd number of equal parts so that one part remains un-cancelled making the point P appear bright.

The condition for first maximum is,

In the same way, condition for nth maximum is,

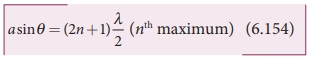
where, n = 0, 1, 2, 3, . . . , is the order of diffraction maximum.

The central maximum is called 0th order maximum. The points of the maximum intensity lie nearly midway between the successive minima.

Here, sinθ gives the angular spread of the diffraction. The position of the minimum or maximum in terms of y may be expressed by replacing sinθ approximated by tanθ, as θ is small, sinθ = tanθ y/D

Where, y is the position of the minimum from the center of the screen and D is the distance between single slit and the screen.

EXAMPLE 6.31

Light of wavelength 500 nm passes through a slit of 0.2 mm wide. The diffraction pattern is formed on a screen 60 cm away. Determine the,

(i) angular spread of central maximum

(ii) the distance between the central maximum and the second minimum.

Solution

λ = 500 nm = 500×10^-9 m; a = 0.2 mm = 0.2×10^-3 m; D = 60 cm = 60×10^-2 m

(i) Equation for diffraction minimum is, a sin θ = nλ

The central maximum is spread up to the first minimum. Hence, n = 1

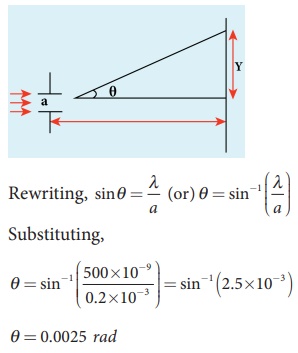
(ii) To find the value of y₁ for central maximum, which is spread up to first minimum with (n = 1) is, a sin θ = λ

To find the value of y₂ for second minimum with (n = 2) is, a sin θ = 2λ

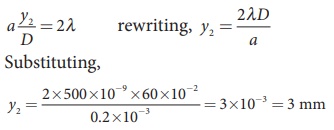
The distance between the central maximum and second minimum is, y₂ – y₁

y₂ – y₁ = 3 mm – 1.5 mm = 1.5 mm

Note: The above calculation shows that in the diffraction pattern caused by single slit, the width of each maximum is equal with central maximum as the double that of others. But the bright and dark fringes are not of equal width.

EXAMPLE 6.32

A monochromatic light of wavelength 5000 Ã… passes through a single slit producing diffraction pattern for the central maximum as shown in the figure. Determine the width of the slit.

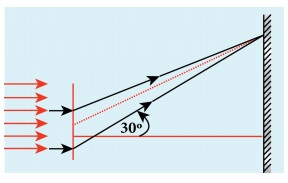
Solution

λ = 5000 Å = 5000×10^-10 m; sin 30º = 0.5; n = 1; a =?

Equation for diffraction minimum is, asin θ = nλ

The central maximum is spread up to the first minimum. Hence, n = 1

Rewriting, a = λ / Sinθ

Substituting, a = 5000×10^−10 / 0.5

a = 1×10^−6 m = 0.001×10^−3m = 0.001mm

3. Discussion on first minimum

Let us consider the condition for first minimum with (n = 1). a sin θ = λ

The first minimum has an angular spread of, sinθ = λ/a

Now, we have special cases to discuss on the above condition.

(i) When a < λ, the diffraction is not possible, because sinθ can never be greater than 1.

(ii) When a ≥ λ, the diffraction is possible.

◗ For a = λ, sinθ = 1 i.e, θ = 90º. That means the first minimum is at 90º. Hence, the central maximum spreads fully in to the geometrically shadowed region leading to bending of the diffracted light to 90º.

◗ For a >> λ, sinθ << 1 i.e, the first minimum will fall within the width of the slit itself. The diffraction will not be noticed at all.

(iii) When a > λ and also comparable, say a = 2λ, sinθ = λ/a = λ/2λ = 1/2; then θ = 30º. These are practical cases where diffraction could be observed effectively.

4. Fresnel’s distance

Fresnel’s distance is the distance up to which the ray optics is valid in terms of rectilinear propagation of light. As there is bending of light in diffraction, the rectilinear propagation of light is violated. But, this bending is not significant till the diffracted ray crosses the central maximum at a distance z as shown in Figure 6.65. Hence, Fresnel’s distance is the distance upto which ray optics is obeyed and beyond which ray optics is not obeyed but, wave optics becomes significant.

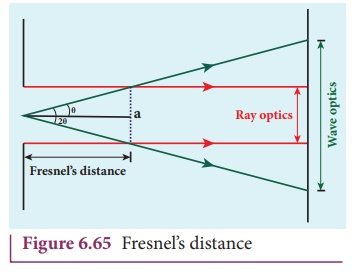
From the diffraction equation for first minimum, sinθ = λ/a; θ = λ/a

From the definition of Fresnel’s distance, sin2θ = a/z; 2θ = a/z

Equating the above two equation gives, λ/a=a/2z

After rearranging, we get Fresnel’s distance z as,

EXAMPLE 6.33

Calculate the distance for which ray optics is good approximation for an aperture of 5 mm and wavelength 500 nm.

Solution

a = 5 mm = 5 × 10^-3 m;

λ = 500nm = 500×10^−9 m; z = ?

Equation for Fresnel’s distance, z = a²/2λ

Substituting,

z = [5 × 10^-3]² / 2×500×10^−9

z = 25 m

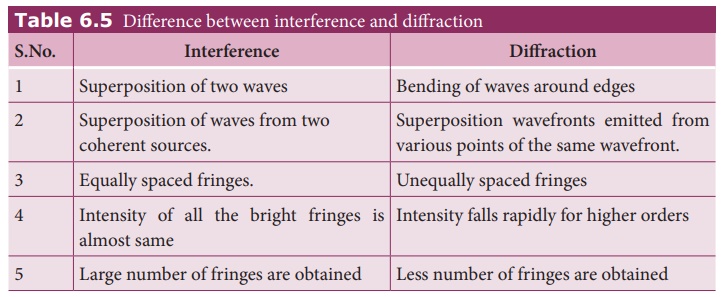
5. Difference between interference and diffraction

It is very difficult to distinguish between interference and diffraction as they both exhibit the wave nature of light. In both the phenomena the light reaches the geometrically shadowed regions and also interferes to produce maximaand minima. Nevertheless, based on the appearance, the differences are given in Table 6.5.

Table 6.5 Difference between interference and diffraction

6. Diffraction in grating

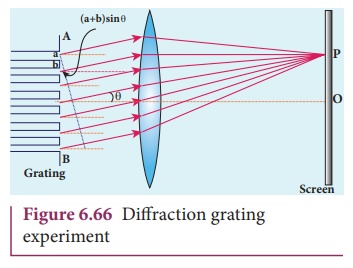
Grating has multiple slits with equal widths of size comparable to the wavelength of diffracting light. Grating is a plane sheet of transparent material on which opaque rulings are made with a fine diamond pointer. The modern commercial grating contains about 6000 lines per centimetre. The rulings act as obstacles having a definite width b and the transparent space between the rulings act as slit of width a. The combined width of a ruling and a slit is called grating element (e = a + b). Points on successive slits separated by a distance equal to the grating element are called corresponding points.

Interference

• Superposition of two waves

• Superposition of waves from two coherent sources.

• Equally spaced fringes.

• Intensity of all the bright fringes is almost same

• Large number of fringes are obtained

Diffraction

• Bending of waves around edges

• Superposition wavefronts emitted from various points of the same wavefront.

• Unequally spaced fringes

• Intensity falls rapidly for higher orders

• Less number of fringes are obtained

A plane transmission grating is represented by AB in Figure 6.66. Let a plane wavefront of monochromatic light with wave length λ be incident normally on the grating. As the slits size is comparable to that of wavelength, the incident light diffracts at the grating.

A diffraction pattern is obtained on the screen when the diffracted waves are focused on a screen using a convex lens. Let us consider a point P at an angle θ with the normal drawn from the center of the grating to the screen. The path difference δ between the diffracted waves from one pair of corresponding points is,

δ = (a + b) sinθ                (6.156)

This path difference is the same for any pair of corresponding points. The point P will be bright, when

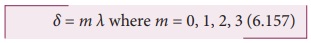
δ = m λ where m = 0, 1, 2, 3             (6.157)

Combining the above two equations, we get,

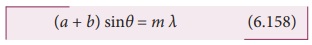
(a + b) sinθ = m λ             (6.158)

Here, m is called order of diffraction.

Condition for zero order maximum, m = 0

For (a + b) sinθ = 0, the position, θ = 0. sinθ = 0 and m = 0. This is called zero order diffraction or central maximum.

Condition for first order maximum, m = 1

If (a + b) sinθ₁ = λ, the diffracted light meet at an angle θ₁ to the incident direction and the first order maximum is obtained.

Condition for second order maximum, m = 2

Similarly, (a + b) sinθ₂ = 2λ forms the second order maximum at the angular position θ₂.

Condition for higher order maximum

On either side of central maxima different higher orders of diffraction maxima are formed at different angular positions.

If we take,

Then, N gives the number of grating elements or rulings drawn per unit width of the grating. Normally, this number N is specified on the grating itself. Now, the equation becomes,

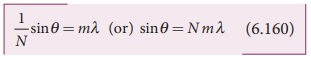
The students should remember that in a single slit experiment the formula, a sinθ = nλ is condition for minimum with n as order of minimum. But, the formula in diffraction grating, sinθ = Nmλ is condition for maxima with m as the order of diffraction.

EXAMPLE 6.34

A diffraction grating consisting of 4000 slits per centimeter is illuminated with a monochromatic light that produces the second order diffraction at an angle of 30°. What is the wavelength of the light used?

Solution

Number of lines per cm = 4000; m = 2;

θ = 30°; λ = ?

Number of lines per unit length,

N = 4000 / 1×10^−2 = 4×10⁵

Equation for diffraction maximum in grating is, sinθ = Nmλ

Rewriting, λ = sinθ / Nm

Substituting,

λ = sin 30º / 4×10⁵×2 =  0.5 / 4×10⁵×2

= 1 / [2×4×10⁵ ×2] = 1 / [16×10⁵]

λ = 6250×10^−10 m = 6250 A^o

EXAMPLE 6.35

A monochromatic light of wavelength of 500 nm strikes a grating and produces fourth order bright line at an angle of 30°. Find the number of slits per centimeter.

Solution

λ = 500 nm = 500×10^-9 m; m = 4;

θ = 30°; number of lines per cm = ?

Equation for diffraction maximum in grating is, sin θ = Nm λ

Rewriting, N = sinθ / mλ

Substituting,

N = 0.5 / 4×500×10^−9 = 1 / 2×4×500×10^−9

N = 2.5×10⁵ lines per meter

number of lines per centimeter = 2.5×10⁵ ×10^−2 = 2500 lines per centimetre

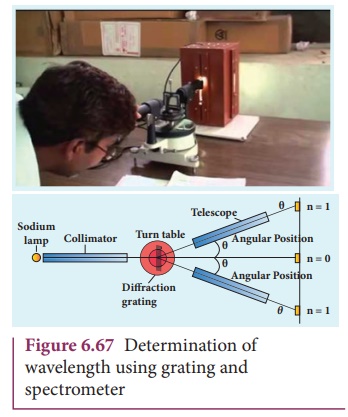
7. Experiment to determine the wavelength of monochromatic light

The wavelength of a spectral line can be very accurately determined with the help of a diffraction grating and a spectrometer. Initially all the preliminary adjustments of the spectrometer are made. The slit of collimator is illuminated by a monochromatic light, whose wavelength is to be determined. The telescope is brought in line with collimator to view the image of the slit. The given plane transmission grating is then mounted on the prism table with its plane perpendicular to the incident beam of light coming from the collimator. The telescope is turned to one side until the first order diffraction image of the slit coincides with the vertical cross wire of the eye piece. The reading of the position of the telescope is noted.

Similarly the first order diffraction image on the other side is made to coincide with the vertical cross wire and corresponding reading is noted. The difference between two positions gives 2θ. Half of its value gives θ, the diffraction angle for first order maximum as shown in Figure 6.67. The wavelength of light is calculated from the equation,

Here, N is the number of rulings per metre in the grating and m is the order of the diffraction image.

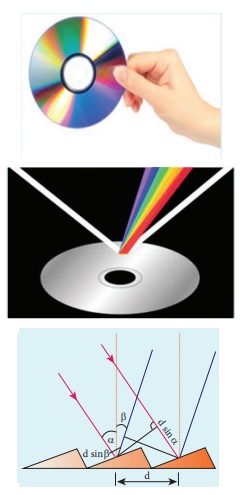
You would have noticed the colourful appearance of the compact disc. On the read/writable side which is polished, there are many narrow circular tracks with widths comparable to the wavelength of visible light. Hence, the diffraction takes place after reflection for incident white light to give colourful appearance. The tracks act as reflecting grating.

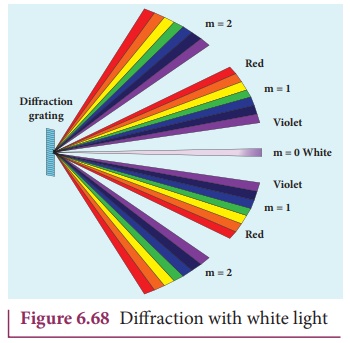
8. Determination of wavelength of different colours

When white light is used, the diffraction pattern consists of a white central maximum and on both sides continuous coloured diffraction patters are formed. The central maximum is white as all the colours meet here constructively with no path difference. As θ increases, the path difference, (a+b)sinθ, passes through condition for maxima of diffraction of different orders for all colours from violet to red. It produces a spectrum of diffraction pattern from violet to red on either side of central maximum as shown in Figure 6.68. By measuring the angle at which these colours appear for various orders of diffraction, the wavelength of different colours could be calculated using the formula,

Here, N is the number of rulings per metre in the grating and m is the order of the diffraction image.

9. Resolution

The effect of diffraction has an adverse impact in the image formation by the optical instruments such as microscope and telescope. For a single rectangular slit, the half angle θ subtended by the spread of central maximum (or position of first minimum) is given by the relation,

a sinθ = λ                 (6.162)

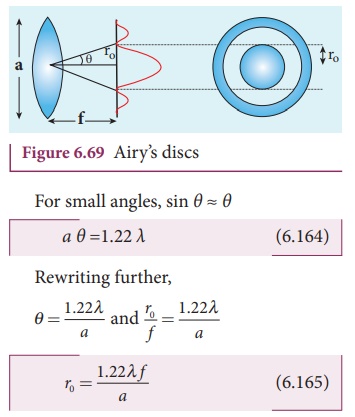
Similar to a rectangular slit, when a circular aperture or opening (like a lens or the iris of our eye) forms an image of a point object, the image formed will not be a point but a diffraction pattern of concentric circles that becomes fainter while moving away from the center as shown in Figure 6.69. These are known as Airy’s discs. The circle of central maximum has the half angular spread given by the equation,

 a sinθ = 1.22 λ           (6.163)

Here, the numerical value 1.22 comes for central maximum formed by circular apertures. This involves higher level mathematics which is avoided in this discussion.

When two point sources close to each another form image on the screen, the diffraction pattern of one point source can overlap with another and produce a blurred image as shown in Figure 6.70(a). To obtain a good image of the two sources, the two point sources must be resolved i.e., the point sources must be imaged in such a way that their images are sufficiently far apart that their diffraction patterns do not overlap. According to Rayleigh’s criterion, for two point objects to be just resolved, the minimum distance between their diffraction images must be in such a way that the central maximum of one coincides with the first minimum of the other and vice versa as shown in Figure 6.70(b). Such an image is said to be just resolved image of the object. The Rayleigh’s criterion is said to be limit of resolution.

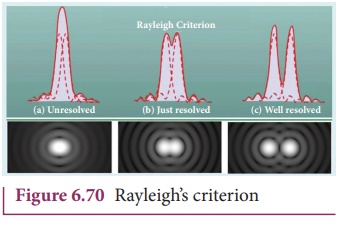
According to Rayleigh’s criterion the two point sources are said to be just resolved when the distance between the two maxima is at least r_o. The angular resolution has a unit in radian (rad) and it is given by the equation,

It shows that the first order diffraction angle must be as small as possible for greater resolution. This further shows that for better resolution, the wavelength of light used must be as small as possible and the size of the aperture of the instrument used must be as large as possible. The Equation 6.165 is used to calculate spacial resolution.

The inverse of resolution is called resolving power. This implies, smaller the resolution, greater is the resolving power of the instrument. The ability of an optical instrument to separate or distinguish small or closely adjacent objects through the image formation is said to be resolving power of the instrument. In general, the term resolution is pertaining to the quality of the image formed and the term resolving power is associated with the ability of the optical instrument.

EXAMPLE 6.36

The optical telescope in the Vainu Bappu observatory at Kavalur has an objective lens of diameter 2.3 m. What is its angular resolution if the wavelength of light used is 589 nm?

Solution

 a = 2.3 m; λ = 589 nm = 589×10^-9 m; θ = ?

The equation for angular resolution is,

 Î¸ = 1.22 λ  / a

Substituting,

 Î¸ = 1.22×589×10^−9 / 2.3 = 321.4×10^−9

 Î¸ = 3.214×10^−7 rad ≈ 0.0011'

Note: The angular resolution of human eye is approximately, 3×10^−4 rad ≈ 1.03'.