Chapter: 12th Physics : UNIT 7 : Wave Optics
Interference: Phase difference and path difference
The phenomenon of addition or superposition of two light waves which produces increase in intensity at some points and decrease in intensity at some other points is called interference of light.
Phase difference and path difference
Phase is the angular position of a vibration. As a wave is progressing, there is a relation between the phase of the vibration and the path travelled by the wave. One can express the phase in terms of path and vice versa. In the path of the wave, one wavelength λ corresponds to a phase of 2π as shown in Figure 6.53. A path difference δ corresponds to a phase difference ϕ as given by the equation,
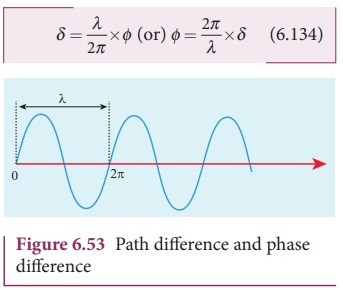
For constructive interference, the phase difference should be, ϕ = 0, 2π, 4π . . . Hence, the path difference must be, δ = 0, λ, 2λ . . . In general, the integral multiples of λ.

For destructive interference, phase difference should be, ϕ = π, 3π, 5π . . . Hence, the path difference must be, δ = λ/2 , 3λ/2 .....
In general, the half integral multiples of λ.
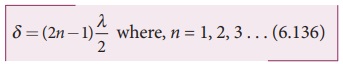
EXAMPLE 6.27
The wavelength of a light is 450 nm. How much phase it will differ for a path of 3 mm?
Solution
The wavelength is, λ = 450 nm = 450×10-9m
Path difference is, δ = 3 mm = 3×10−3m
Relation between phase difference and path difference is, ϕ = 2π/λ ×δ
Substituting,
ϕ = [ 2π / 450×10-9 ] ×3×10−3 = (π/75) ×106
ϕ = (π/75) ×106 rad
Related Topics