Wave Optics | Physics - Solved Example Numerical Problems | 12th Physics : UNIT 7 : Wave Optics
Chapter: 12th Physics : UNIT 7 : Wave Optics
Solved Example Numerical Problems
Wave Optics - Numerical Problems Questions with Answers, Solution
Wave Nature of Light - Numerical Problems Questions with Answers, Solution
EXAMPLE Q
The wavelength of light from sodium source in vacuum is 5893├ģ.What are its (a) wavelength, (b) speed and (c) frequency when this light travels in water which has a refractive index of 1.33.
Solution
The refractive index of vacuum, n1 = 1
The wavelength in vacuum, ╬╗1 = 5893 ├ģ.
The speed in vacuum, c = 3 ├Ś 108 m sŌĆō1
The refractive index of water, n2 = 1.33
The wavelength of light in water, ╬╗2
The speed of light in water, v2
(a) The equation relating the wavelength and refractive index is,

(b) The equation relating the speed and refractive index is,
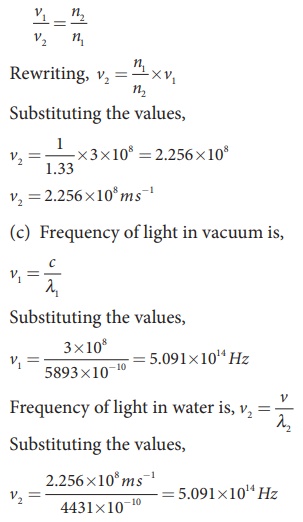
The results show that the frequency remains same in all media.
Interference - Numerical Problems Questions with Answers, Solution
EXAMPLE Q
Two light sources with amplitudes 5 units and 3 units respectively interfere with each other. Calculate the ratio of maximum and minimum intensities.
Solution
Amplitudes, a1 = 5, a2 = 3
Resultant amplitude,

EXAMPLE Q
Two light sources of equal amplitudes interfere with each other. Calculate the ratio of maximum and minimum intensities.
Solution
Let the amplitude be a.
The intensity is, I ŌłØ ┬Ą 4a2 cos2(ŽĢ/ 2)
or I = 4I0 cos2(ŽĢ/2)
Resultant intensity is maximum when,
ŽĢ = 0, cos0 = 1, Imax ŌłØ 4a2
Resultant amplitude is minimum when,
ŽĢ = ŽĆ, cos(ŽĆ/2) = 0, Imin = 0
Imax : Imin = 4a2 : 0
EXAMPLE Q
Two light sources have intensity of light as I0. What is the resultant intensity at a point where the two light waves have a phase difference of ŽĆ/3?
Solution
Let the intensities be I0.
The resultant intensity is, I = 4I0cos2(ŽĢ/2)
Resultant intensity when, ŽĢ = ŽĆ / 3, is
I = 4I0 cos2 (ŽĆ/6)
I = 4Io (ŌłÜ3/2)2 = 3Io
EXAMPLE Q
The wavelength of a light is 450 nm. How much phase it will differ for a path of 3 mm?
Solution
The wavelength is, ╬╗ = 450 nm = 450├Ś10-9m
Path difference is, ╬┤ = 3 mm = 3├Ś10ŌłÆ3m
Relation between phase difference and path difference is, ŽĢ = 2ŽĆ/╬╗ ├Ś╬┤
Substituting,
ŽĢ = [ 2ŽĆ / 450├Ś10-9 ] ├Ś3├Ś10ŌłÆ3 = (ŽĆ/75) ├Ś106
ŽĢ = (ŽĆ/75) ├Ś106 rad
EXAMPLE Q
In YoungŌĆÖs double slit experiment, the two slits are 0.15 mm apart. The light source has a wavelength of 450 nm. The screen is 2 m away from the slits.
(i) Find the distance of the second bright fringe and also third dark fringe from the central maximum.
(ii) Find the fringe width.
(iii) How will the fringe pattern change if the screen is moved away from the slits?
(iv) What will happen to the fringe width if the whole setup is immersed in water of refractive index 4/3.
Solution
d = 0.15 mm = 0.15├Ś 10-3 m; D = 2 m;
╬╗ = 450 nm = 450 ├Ś 10-9 m; n = 4/3
(i) Equation for nth bright fringe is,

(ii) Equation for fringe width is,
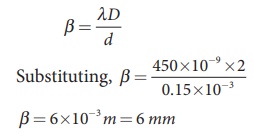
(iii) The fringe width will increase as D is increased,
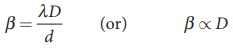
(iv) The fringe width will decrease as the setup is immersed in water of refractive index 4/3
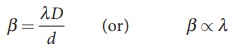
The wavelength will decrease refractive index n times.
Hence, ╬▓ ŌłØ ╬╗ and ╬▓ŌĆÖ ŌłØ ╬╗ŌĆÖ
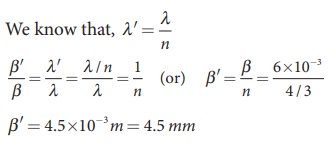
EXAMPLE Q
Two lights of wavelengths 560 nm and 420 nm are used in YoungŌĆÖs double slit experiment. Find the least distance from the central fringe where the bright fringe of the two wavelengths coincides. Given D = 1 m and d = 3 mm.
Solution
╬╗ = 560 nm = 560├Ś10ŌłÆ9 m;
╬╗2 = 420 nm = 420├Ś10ŌłÆ9 m;
D = 1 m;d = 3 mm = 3├Ś10ŌłÆ3 m
For a given y, n and ╬╗ are inversely proportional.
Let nth order bright fringe of ╬╗1 coincides with (n+1)th order bright fringe of ╬╗2.

Thus, the 3rd bright fringe of ╬╗1 and 4th bright fringe of ╬╗2 coincide at the least distance y.
The least distance from the central fringe where the bright fringes of the two wavelengths coincides is, yn = n [(╬╗D)/d]
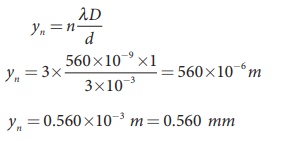
EXAMPLE Q
Find the minimum thickness of a film of refractive index 1.25, which will strongly reflect the light of wavelength 589 nm. Also find the minimum thickness of the film to be anti-reflecting.
Solution
╬╗ = 589 nm = 589├Ś10ŌłÆ9 m
For the film to have strong reflection, the reflected waves should interfere constructively. The least optical path difference introduced by the film should be ╬╗/2. The optical path difference between the waves reflected from the two surfaces of the film is 2┬Ąd. Thus, for strong reflection, 2┬Ąd = ╬╗/2 [As given in equation 6.145. with n = 1]
Rewriting, d = ╬╗/4╬╝
Substituting, d = [589├Ś109] / [4├Ś1.25] = 117.8├Ś10ŌłÆ9
d = 117.8├Ś10ŌłÆ9 = 117.8 nm
For the film to be anti-reflecting, the reflected rays should interfere destructively. The least optical path difference introduced by the film should be ╬╗. The optical path difference between the waves reflected from the two surfaces of the film is 2┬Ąd. For strong reflection, 2┬Ąd = ╬╗ [As given in equation 6.146. with n = 1].
Rewriting, d = ╬╗/2╬╝
Substituting, d = [589├Ś109] / [2├Ś1.25] = 235.6├Ś10ŌłÆ9
d = 235.6├Ś10ŌłÆ9 = 235.6 nm
Diffraction - Numerical Problems Questions with Answers, Solution
EXAMPLE Q
Light of wavelength 500 nm passes through a slit of 0.2 mm wide. The diffraction pattern is formed on a screen 60 cm away. Determine the,
(i) angular spread of central maximum
(ii) the distance between the central maximum and the second minimum.
Solution
╬╗ = 500 nm = 500├Ś10-9 m; a = 0.2 mm = 0.2├Ś10-3 m; D = 60 cm = 60├Ś10-2 m
(i) Equation for diffraction minimum is, a sin ╬Ė = n╬╗
The central maximum is spread up to the first minimum. Hence, n = 1
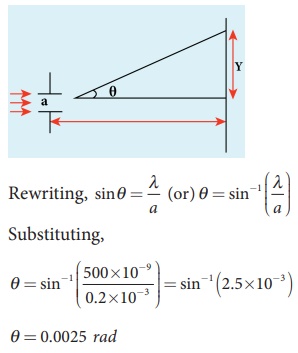
(ii) To find the value of y1 for central maximum, which is spread up to first minimum with (n = 1) is, a sin ╬Ė = ╬╗

To find the value of y2 for second minimum with (n = 2) is, a sin ╬Ė = 2╬╗
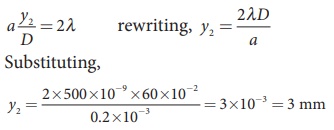
The distance between the central maximum and second minimum is, y2 ŌĆō y1
y2 ŌĆō y1 = 3 mm ŌĆō 1.5 mm = 1.5 mm

Note: The above calculation shows that in the diffraction pattern caused by single slit, the width of each maximum is equal with central maximum as the double that of others. But the bright and dark fringes are not of equal width.
EXAMPLE Q
A monochromatic light of wavelength 5000 ├ģ passes through a single slit producing diffraction pattern for the central maximum as shown in the figure. Determine the width of the slit.
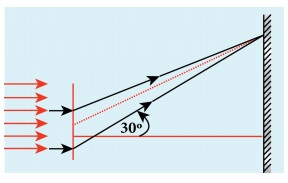
Solution
╬╗ = 5000 ├ģ = 5000├Ś10-10 m; sin 30┬║ = 0.5; n = 1; a =?
Equation for diffraction minimum is, asin ╬Ė = n╬╗
The central maximum is spread up to the first minimum. Hence, n = 1
Rewriting, a = ╬╗ / Sin╬Ė
Substituting, a = 5000├Ś10ŌłÆ10 / 0.5
a = 1├Ś10ŌłÆ6 m = 0.001├Ś10ŌłÆ3m = 0.001mm
EXAMPLE Q
Calculate the distance for which ray optics is good approximation for an aperture of 5 mm and wavelength 500 nm.
Solution
a = 5 mm = 5 ├Ś 10-3 m;
╬╗ = 500nm = 500├Ś10ŌłÆ9 m; z = ?
Equation for FresnelŌĆÖs distance, z = a2/2╬╗
Substituting,
z = [5 ├Ś 10-3]2 / 2├Ś500├Ś10ŌłÆ9
z = 25 m
EXAMPLE Q
A diffraction grating consisting of 4000 slits per centimeter is illuminated with a monochromatic light that produces the second order diffraction at an angle of 30┬░. What is the wavelength of the light used?
Solution
Number of lines per cm = 4000; m = 2;
╬Ė = 30┬░; ╬╗ = ?
Number of lines per unit length,
N = 4000 / 1├Ś10ŌłÆ2 = 4├Ś105
Equation for diffraction maximum in grating is, sin╬Ė = Nm╬╗
Rewriting, ╬╗ = sin╬Ė / Nm
Substituting,
╬╗ = sin 30┬║ / 4├Ś105├Ś2 = 0.5 / 4├Ś105├Ś2
= 1 / [2├Ś4├Ś105 ├Ś2] = 1 / [16├Ś105]
╬╗ = 6250├Ś10ŌłÆ10 m = 6250 Ao
EXAMPLE Q
A monochromatic light of wavelength of 500 nm strikes a grating and produces fourth order bright line at an angle of 30┬░. Find the number of slits per centimeter.
Solution
╬╗ = 500 nm = 500├Ś10-9 m; m = 4;
╬Ė = 30┬░; number of lines per cm = ?
Equation for diffraction maximum in grating is, sin ╬Ė = Nm ╬╗
Rewriting, N = sin╬Ė / m╬╗
Substituting,
N = 0.5 / 4├Ś500├Ś10ŌłÆ9 = 1 / 2├Ś4├Ś500├Ś10ŌłÆ9
N = 2.5├Ś105 lines per meter
number of lines per centimeter = 2.5├Ś105 ├Ś10ŌłÆ2 = 2500 lines per centimetre
EXAMPLE Q
The optical telescope in the Vainu Bappu observatory at Kavalur has an objective lens of diameter 2.3 m. What is its angular resolution if the wavelength of light used is 589 nm?
Solution
a = 2.3 m; ╬╗ = 589 nm = 589├Ś10-9 m; ╬Ė = ?
The equation for angular resolution is,
╬Ė = 1.22 ╬╗ / a
Substituting,
╬Ė = 1.22├Ś589├Ś10ŌłÆ9 / 2.3 = 321.4├Ś10ŌłÆ9
╬Ė = 3.214├Ś10ŌłÆ7 rad Ōēł 0.0011'
Note: The angular resolution of human eye is approximately, 3├Ś10ŌłÆ4 rad Ōēł 1.03'.
Polarisation Techniques - Numerical Problems Questions with Answers, Solution
EXAMPLE Q
Two polaroids are kept with their transmission axes inclined at 30┬║. Unpolarised light of intensity I falls on the first polaroid. Find out the intensity of light emerging from the second polaroid.
Solution
As the intensity of the unpolarised light falling on the first polaroid is I, the intensity of polarized light emerging will be, I0 = ( I/2 ).
Let I ŌĆś be the intensity of light emerging from the second polaroid.
MalusŌĆÖ law, I ŌĆ▓ = I0 cos2 ╬Ė
Substituting,
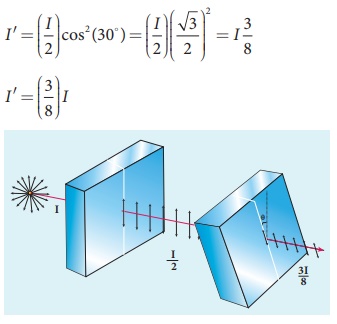
EXAMPLE Q
Two polaroids are kept crossed (transmission axes at 90┬║) to each other.
(i) What will be the intensity of the light coming out from the second polaroid when an unpolarised light of intensity I falls on the first polaroid?
(ii) What will be the intensity of light coming out from the second polaroid if a third polaroid is kept at 45┬║ inclination to both of them.
Solution
(i) As the intensity of the unpolarised light falling on the first polaroid is I, the intensity of polarized light emerging from it will be I0 = (I/2).
Let IŌĆś be the intensity of light emerging from the second polaroid.
MalusŌĆÖ law, I ŌĆ▓ = I0 cos2 ╬Ė
Here ╬Ė is 90┬║ as the transmission axes are perpendicular to each other.
Substituting,
I0 = ( I/2 ) cos2 (90┬║)= 0
[Ōł┤ cos(90┬║ )= 0]
No light comes out from the second polaroid.
(ii) Let the first polaroid be P1 and the second polaroid be P2. They are oriented at 90┬║. The third polaroid P3 is introduced between them at 45┬║. Let I ŌĆś be the intensity of light emerging from P3.
Angle between P1 and P3 is 45┬║. The intensity of light coming out from P3 is, I ŌĆ▓ = I0 cos2 ╬Ė
Substituting,

Angle between P3 and P2 is 45┬║. Let IŌĆØ is the intensity of light coming out from P2 I ŌĆ▓ŌĆ▓ = I ŌĆ▓ cos2 ╬Ė
Here, the intensity of polarized light existing between P3 and P2 is 1/4.
Substituting,

EXAMPLE Q
Find the polarizing angles for (i) glass of refractive index 1.5 and (ii) water of refractive index 1.33.
Solution
BrewsterŌĆÖs law, tanip = n
For glass, tanip = 1.5; ip = tanŌłÆ11.5; ip = 56.3┬║
Forwater, tanip = 1.33; ip = tanŌłÆ11.33; ip = 53.1┬║
EXAMPLE Q
What is the angle at which a glass plate of refractive index 1.65 is to be kept with respect to the horizontal surface so that an unpolarised light travelling horizontal after reflection from the glass plate is found to be plane polarised?
Solution
n = 1.65
BrewsterŌĆÖs law, tanip = n
tanip = 1.65; ip = tanŌłÆ11.65; ip = 58.80
The inclination with the horizontal surface is, (900 ŌłÆ58.80 ) = 31.20
Simple microscope - Numerical Problems Questions with Answers, Solution
EXAMPLE Q
A man with a near point of 25 cm reads a book with small print using a magnifying glass, a convex lens of focal length 5 cm. (a) What is the closest and the farthest distance at which he should keep the lens from the page so that he can read the book when viewing through the magnifying glass? (b) What is the maximum and the minimum angular magnification (magnifying power) possible using the above simple microscope?
Solution
D = 25 cm; f = 5 cm;
For closest object distance, u; the image distance, v is, ŌĆō25 cm. (near point focusing)
For farthest object distance, uŌĆÖ; the corresponding image distance, vŌĆÖ is, vŌĆÖ = Ōł× (normal focusing)
(a) To find closest image distance, lens equation, 1/v ŌĆō 1/u = 1/f
Rewriting for closest object distance, 1/u = 1/v - 1/f
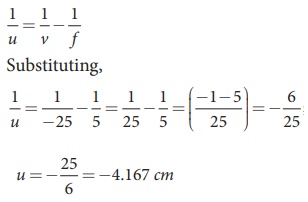
The closest distance at which the person should can keep the book is, u = ŌĆō4.167 cm
To find farthest object distance, lens equation is, 1/vŌĆÖ ŌĆō 1/uŌĆÖ = 1/fŌĆÖ
Rewriting for farthest object distance, 1/uŌĆÖ = 1/vŌĆÖ - 1/fŌĆÖ
Substituting, 1/uŌĆÖ = 1/Ōł× - 1/5; u = ŌłÆ5 cm
The farthest distance at which the person can keep the book is, uŌĆ▓ = ŌłÆ5 cm
(b) To find magnification in near point focusing, m = 1+ D/f = 1+ 25/5 = 6
To find magnification in normal focusing,
m = D/f = 25/5 = 5
Compound microscope - Numerical Problems Questions with Answers, Solution
EXAMPLE Q
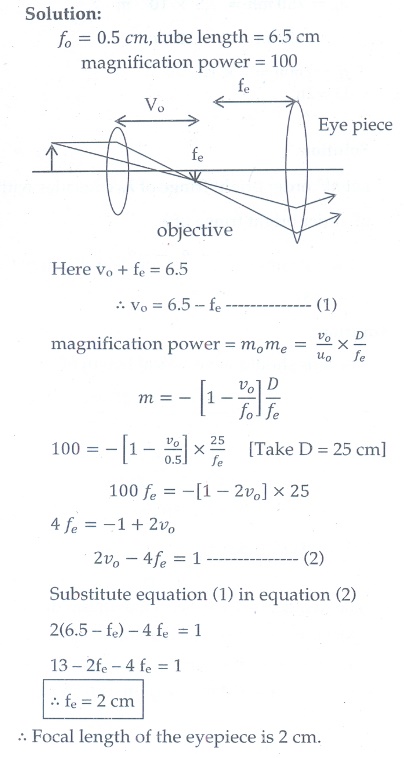
A microscope has an objective and eyepiece of focal lengths 5 cm and 50 cm respectively with tube length 30 cm. Find the magnification of the microscope in the (i) near point and (ii) normal focusing.
Solution
f0 = 5cm = 5├Ś10ŌłÆ2 m; fe = 50cm = 50├Ś10ŌłÆ2 m;
L = 30cm = 30├Ś10ŌłÆ2 m; D = 25cm = 25├Ś10ŌłÆ2 m
(i) The total magnification m in near point focusing is, m = mome
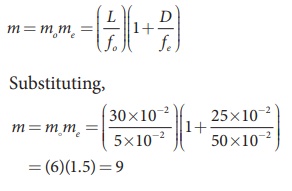
(ii) The total magnification m in normal focusing is, m = mome

Astronomical telescope - Numerical Problems Questions with Answers, Solution
EXAMPLE Q
A small telescope has an objective lens of focal length 125 cm and an eyepiece of focal length 2 cm. What is the magnification of the telescope? What is the separation between the objective and the eyepiece? Two stars separated by 1ŌĆÖ will appear at what separation when viewed through the telescope?
Solution
fo = 125 cm; fe = 2 cm; m = ?; L = ?; ╬Ėi = ?
Equation for magnification of telescope, m = fo/ fe
Substituting, m = 125/2 = 62.5
Equation for approximate length of telescope, L = fo+ fe
Substituting, L = 125+2 = 127 cm = 1.27 m
Equation for angular magnification, m = ╬Ėi/╬Ė0
Rewriting, ╬Ėi = m├Ś╬Ė0
Substituting,
╬Ėi = 62.5├Ś1ŌĆ▓ = 62.5ŌĆ▓ = 62.5/60 = 1.04┬║
Optical Instruments: The eye - Numerical Problems Questions with Answers, Solution
EXAMPLE Q
Calculate the power of the lens of the spectacles necessary to rectify the defect of nearsightedness for a person who could see clearly only up to a distance of 1.8 m.
Solution
The maximum distance the person could see is, x = 1.8 m.
The lens should have a focal length of, f = ŌĆōx m = ŌĆō1.8 m.
It is a concave or diverging lens.
The power of the lens is,
P = ŌłÆ 1/1.8 m
= ŌłÆ0.56 diopter
EXAMPLE Q
A person has farsightedness with the minimum distance he could see clearly is 75 cm. Calculate the power of the lens of the spectacles necessary to rectify the defect.
Solution
The minimum distance the person could see clearly is, y = 75 cm.
The lens should have a focal length of,
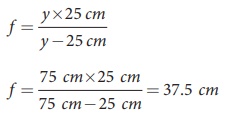
f = y├Ś25 cm / y-25 cm
f = [75 cm├Ś25 cm ] / [75 cm ŌłÆ25 cm] = 37.5 cm
It is a convex or converging lens.
The power of the lens is,
P = 1 / 0.375 m = 2.67 diopter
Numerical Problems
1. The ratio of maximum and minimum intensities in an interference pattern is 36:1. What is the ratio of the amplitudes of the two interfering waves?
[Ans: 7:5]

2. In YoungŌĆÖs double slit experiment, 62 fringes are seen in visible region for sodium light of wavelength 5893 ├ģ. If violet light of wavelength 4359 ├ģ is used in place of sodium light, then what is the number of fringes seen? [Ans: 84]

3. Light of wavelength 600 nm that falls on a pair of slits producing interference pattern on a screen in which the bright fringes are separated by 7.2 mm. What must be the wavelength of another light which produces bright fringes separated by 8.1 mm with the same apparatus?
[Ans: 675 nm]

4. A beam of light of wavelength 600 nm from a distant source falls on a single slit 1 mm wide and the resulting diffraction pattern is observed on a screen 2 m away. What is the distance between the first dark fringe on either side of the central bright fringe?
[Ans: 2.4 mm]

5. Light of wavelength of 5000 ├ģ produces diffraction pattern of the single slit of width 2.5 ┬Ąm. What is the maximum order of diffraction possible?
[Ans: 5]

6. I0 is the intensity of light existing between two cross Polaroids kept with their axes perpendicular to each other. A third polaroid is introduced between them. What must be the angle between the axes of first and the newly introduced polaroid to ge the maximum light from the whol arrangement?
[Ans: 45┬░]

7. An unpolarised light of intensity 32 Wm-2 passes through three Polaroids such that the axes of the first and the last Polaroids are at 90┬░. What is the angle between the axes of the first and middle Polaroids so that the emerging light has an intensity of only 3 Wm-┬▓?
[Ans: 30┬░]

8. The reflected light is found to be plane polarised when an unpolarized light falls on a denser medium at 60┬░ with the normal. Find the angle of refraction and critical angle of incidence for total internal reflection in the denser to rarer medium reflection.
[Ans: 30┬░, 35.15┬░]

9. The near point and the far point for a person are 50 cm and 500 cm, respectively. Calculate the power of the lens the person should wear to read a book held in hand at 25 cm. What maximum distance is clearly visible for the person with this lens on the eye?
[Ans: 2D, 45.45 cm]

10. A compound microscope has a magnifying power of 100 when the image is formed at infinity. The objective has a focal length of 0.5 cm and the tube length is 6.5 cm. What is the focal length of the eyepiece.
[Ans: 2 cm]
Related Topics