Polarisation Techniques

Polarisation Techniques

The unpolarised light can be polarised by several techniques. Here, we are discussing the following four methods,

(i) polarisation by selective absorption

(ii) polarisation by reflection

(iii) polarisation by double refraction

(iv) polarisation by scattering.

1. Polarisation by selective absorption

Selective absorption is the property of a material which transmits waves whose electric fields vibrate in a plane parallel to a certain direction of orientation and absorbs all other waves. The polaroids or polarisers are thin commercial sheets which make use of the property of selective absorption to produce an intense beam of plane polarised light. Selective absorption is also called as dichroism.

In 1932, an American scientist Edwin Land developed polarisers in the form of sheets. Tourmaline is a natural polarising material. Polaroids are also made artificially. It was discovered that small needle shaped crystals of quinine iodosulphate have the property of polarising light. A number of these crystals with their axes parallel to one another packed in between two transparent plastic sheets serve as a good polaroid. Recently new types of polaroids are prepared in which thin film of polyvinyl alcohol is used. These are colourless crystals which transmit more light, and give better polarisation. Polaroids have many applications as the one shown in Figure 6.73.

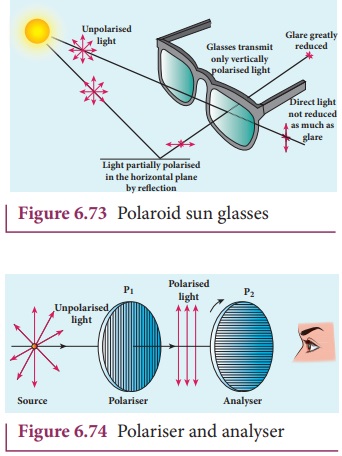
Polariser and analyser

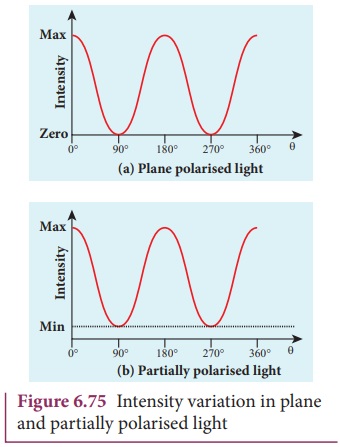
Let us consider an unpolarised beam of light. The vibrations can be in all possible directions all of them being perpendicular to the direction of propagation as shown in Figure 6.74. When this light passes through polaroid P₁ the vibrations are restricted to only one plane. The emergent beam can be further passed through another polaroid P₂. If the polaroid P₂ is rotated about the ray of light as axis, for a particular position of P₂ the intensity is maximum. When the polaroid P₂ is rotated from this position the intensity starts decreasing. There is complete extinction of the light when P₂ is rotated through 90º. On further rotation of P₂ the light reappears and the intensity increases and becomes a maximum for a further rotation through 90 º. The light  coming out from polaroid P₁ is said to be plane polarised. The Polaroid (here P₁) which plane polarises the unpolarised light passing through it is called a polariser. The polaroid (here P₂) which is used to examine whether a beam of light is polarised or not is called an analyser.

If the intensity of the unpolarised light is I then the intensity of plane polarised light will be (I/2). The other half of intensity is restricted by the polariser.

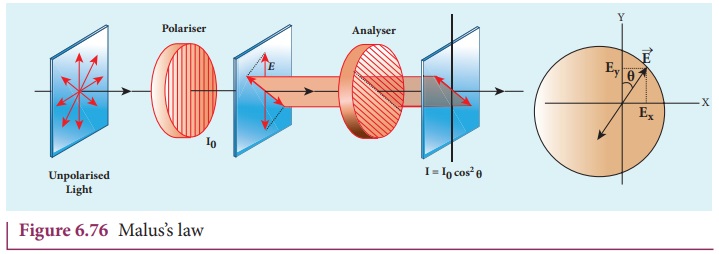
Plane and partially polarised light

In plane polarised light the intensity varies from maximum to zero for every rotation of 90º of the analyser as shown in Figure 6.75(a). This is because the vibrations are allowed in one axis and completely restricted in the perpendicular axis. On the other hand, if the intensity of light varies between maximum and minimum for every rotation of 90º of the analyser, the light is said to be partially polarised light as shown in Figure 6.75(b). This is because the light is not fully restricted in that particular axis which shows a minimum intensity.

Malus’ law

When a plane polarised light is seen through an analyser, the intensity of transmitted light varies as the analyser is rotated through an angle perpendicular to the incident direction. In 1809, French Physicist E.N Malus discovered that when a beam of plane polarised light of intensity I₀ is incident on an analyser, the light transmitted of intensity I from the analyser varies directly as the square of the cosine of the angle θ between the transmission axis of polariser and analyser as shown in Figure 6.76. This is known as Malus’ law.

I = I₀ cos² θ (6.167)

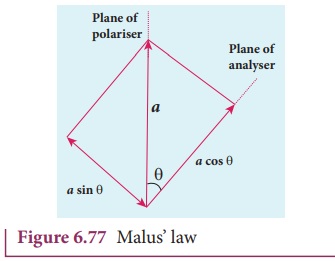
The proof of Malus’s law is as follows. Let us consider the plane of polariser and analyser are inclined to each other at an angle θ is as shown in Figure 6.77. Let I₀ be the intensity and a be the amplitude of the electric vector transmitted by the polariser. The amplitude a of the incident light has two rectangular components, acosθ and asinθ which are the parallel and perpendicular components to the axis of transmission of the analyser.

Only the component acosθ will be transmitted by the analyser. The intensity of light transmitted from the analyser is proportional to the square of the component of the amplitude transmitted by the analyser.

I ∝ (a cosθ)²

I =k(a cosθ)²

Where k is constant of proportionality.

I =ka² cos² θ

I = I₀ cos² θ

Where, I₀ = ka² is the maximum intensity of light transmitted from the analyser.

The following are few special cases.

Case (i) When θ = 0º, cos 0 º  = 1, I = I₀

When the transmission axis of polarizer is along that of the analyser, the intensity of light transmitted from the analyser is equal to the incident light that falls on it from the polariser.

Case (ii) When θ = 90º, cos 90º = 0, I = 0

When the transmission axes of polarizer and analyser are perpendicular to each other, the intensity of light transmitted from the analyser is zero.

EXAMPLE 6.37

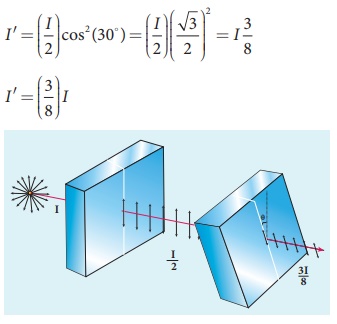
Two polaroids are kept with their transmission axes inclined at 30º. Unpolarised light of intensity I falls on the first polaroid. Find out the intensity of light emerging from the second polaroid.

Solution

As the intensity of the unpolarised light falling on the first polaroid is I, the intensity of polarized light emerging will be, I₀ = ( I/2 ).

Let I ‘ be the intensity of light emerging from the second polaroid.

Malus’ law, I ′ = I₀ cos² θ

Substituting,

EXAMPLE 6.38

Two polaroids are kept crossed (transmission axes at 90º) to each other.

(i) What will be the intensity of the light coming out from the second polaroid when an unpolarised light of intensity I falls on the first polaroid?

(ii) What will be the intensity of light coming out from the second polaroid if a third polaroid is kept at 45º inclination to both of them.

Solution

(i) As the intensity of the unpolarised light falling on the first polaroid is I, the intensity of polarized light emerging from it will be I₀ = (I/2).

Let I‘ be the intensity of light emerging from the second polaroid.

Malus’ law, I ′ = I₀ cos² θ

Here θ is 90º as the transmission axes are perpendicular to each other.

Substituting,

I₀ = ( I/2 ) cos² (90º)= 0

[∴ cos(90º )= 0]

No light comes out from the second polaroid.

(ii) Let the first polaroid be P₁ and the second polaroid be P₂. They are oriented at 90º. The third polaroid P₃ is introduced between them at 45º. Let I ‘ be the intensity of light emerging from P₃.

Angle between P₁ and P₃ is 45º. The intensity of light coming out from P₃ is, I ′ = I₀ cos² θ

Substituting,

Angle between P₃ and P₂ is 45º. Let I” is the intensity of light coming out from P₂ I ′′ = I ′ cos² θ

Here, the intensity of polarized light existing between P₃ and P₂ is 1/4.

Substituting,

Uses of polaroids

• Polaroids are used in goggles and cameras to avoid glare of light.

• Polaroids are useful in three dimensional motion pictures i.e., in holography.

• Polaroids are used to improve contrast in old oil paintings.

• Polaroids are used in optical stress analysis.

• Polaroids are used as window glasses to control the intensity of incoming light.

• Polarised laser beam acts as needle to read/write in compact discs (CDs).

• Polaroids produce polarised lights to be used in liquid crystal display (LCD).

2. Polarisation by reflection

The simplest method of producing plane polarised light is by reflection. Consider a beam of unpolarised light AB is incident at any angle on the reflecting glass surface XY.

Vibrations in AB which are parallel to the plane of the diagram are shown by arrows. The vibrations which are perpendicular to the plane of the diagram and parallel to the reflecting surface are shown by dots in Figure 6.78. A part of the light is reflected along BC, and the rest is refracted along BD. On examining the reflected beam BC with an analyser, it is found that the ray is partially plane polarised. When the light is allowed to be incident at a particular angle the reflected beam is found to be plane polarised. The angle of incidence at which the reflected beam is plane polarised is called polarising angle i_p.

Brewster’s Law

In 1808, Malus discovered that when ordinary light is incident on the surface of a transparent medium, the reflected light is partially plane polarised. The extent of polarisation depends on the angle of incidence. For a particular angle of incidence, the reflected light is found to be plane polarised. The angle of incidence at which a beam of unpolarised light falling on a transparent surface is reflected as a beam of plane polarised light is called polarising angle or Brewster’s angle. It is denoted by i_p.

Further, the British Physicist, Sir. David Brewster found that at the incidence of polarising angle, the reflected and transmitted rays are perpendicular to each other. Suppose, i_p is the polarising angle and r_p is the corresponding angle of refraction. Then from Figure 6.82,

i_p + 90⁰ + r_p = 180⁰ (6.168)

r_p = 90⁰ −i_p (6.169)

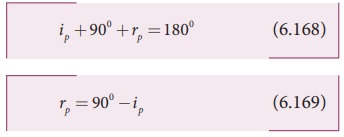
From Snell’s law, the refractive index of the transparent medium is,

where n is the refractive index of the medium with respect to air.

Substituting the value of r_p from Equation 6.163, we get,

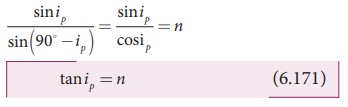
This relation is known as Brewster’s law. The law states that the tangent of the polarising angle for a transparent medium is equal to its refractive index. The value of Brewster’s angle depends on the nature of the transparent refracting medium and the wavelength of light used.

EXAMPLE 6.39

Find the polarizing angles for (i) glass of refractive index 1.5 and (ii) water of refractive index 1.33.

Solution

Brewster’s law, tani_p = n

For glass, tani_p = 1.5; i_p = tan⁻¹1.5; i_p = 56.3º

Forwater, tani_p = 1.33; i_p = tan⁻¹1.33; i_p = 53.1º

Pile of plates

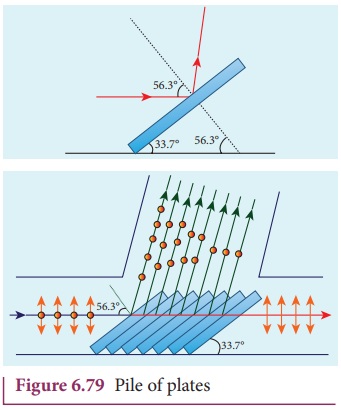
The phenomenon of polarisation by reflection is used in the construction of pile of plates. It consists of a number of glass plates placed one over the other in a tube as shown in Figure 6.79. The plates are inclined at an angle of 33.7º(90º -56.3º ) to the axis of the tube. A beam of unpolarised light is allowed to fall on the pile of plates along the axis of the tube. So, the angle of incidence of light will be at 56.3º which is the polarising angle for glass. The vibrations perpendicular to the plane of incidence are reflected at each surface and those parallel to it are transmitted. The larger the number of surfaces, the greater is the intensity of the reflected plane polarised light. The pile of plates is used as a polarizer and also as an analyser.

EXAMPLE 6.40

What is the angle at which a glass plate of refractive index 1.65 is to be kept with respect to the horizontal surface so that an unpolarised light travelling horizontal after reflection from the glass plate is found to be plane polarised?

Solution

n = 1.65

Brewster’s law, tani_p = n

tani_p = 1.65; i_p = tan⁻¹1.65; i_p = 58.8⁰

The inclination with the horizontal surface is, (90⁰ −58.8⁰ ) = 31.2⁰

3. Polarisation by double refraction

Erasmus Bartholinus, a Danish physicist discovered that when a ray of unpolarised light is incident on a calcite crystal, two refracted rays are produced. Hence, two images of a single object are formed. This phenomenon is called double refraction as shown in Figure 6.80. Double refraction is also called birefringence. This phenomenon  is also exhibited by several other crystals like quartz, mica etc.

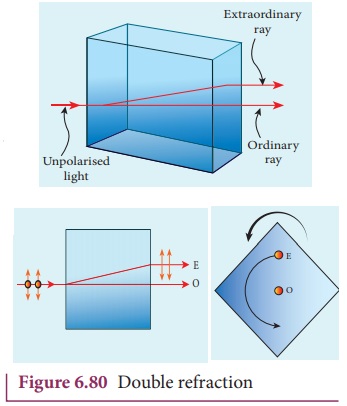
When an ink dot on a sheet of paper is viewed through a calcite crystal, two images will be seen. On rotating the crystal, one image remains stationary, while the other rotates around the first. The stationary image is known as the ordinary image O, produced by the refracted rays which obey the laws of refraction, called as ordinary rays. The other image is extraordinary image E, produced by the refracted rays which do not obey the laws of refraction, called as extraordinary rays. The extraordinary ray is found to be plane polarised. Inside a double refracting crystal the ordinary ray travels with same velocity in all directions and the extra ordinary ray travels with different velocities along different directions. A point source inside a refracting crystal produces spherical wavefront corresponding to ordinary ray and elliptical wavefront corresponding to extraordinary ray. Inside the crystal, there is a particular direction in which both the rays travel with same velocity. This direction is called optic axis. Along the optic axis, the refractive index is same for both the rays and there is no double refraction along this direction.

Types of optically active crystals

Crystals like calcite, quartz, tourmaline and ice having only one optic axis are called uniaxial crystals.

Crystals like mica, topaz, selenite and aragonite having two optic axes are called biaxial crystals.

Nicol prism

Nicol prism is an optical device incorporated in optical instruments both for producing and analysing plane polarised light. The construction of a Nicol prism is based on the phenomenon of Double refraction and was designed by William Nicol in 1828.

One of the most common forms of the Nicol prism is made by taking a calcite crystal which is a double refracting crystal with its length three times its breadth. As shown in Figure 6.81, ABCD represents the principal section of a calcite crystal. It is cut into two halves along the diagonal so that their face angles are 72º and 108º. The two halves are joined together by a layer of canada balsam, a transparent cement.

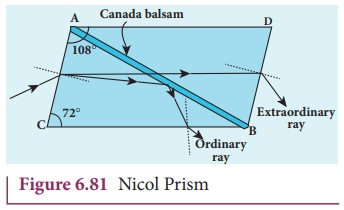
Let us consider a ray of unpolarised light from monochromatic source such as a sodium vapour lamp is incident on the face AC of the Nicol prism. Double refraction takes place and the ray is split into ordinary and extraordinary rays. They travel with different velocities. The refractive index of the crystal for the ordinary ray (monochromatic sodium light) is 1.658 and for extraordinary ray is 1.486. The refractive index of canada balsam is 1.523. Canada balsam does not polarise light.

The ordinary ray is total internally reflected at the layer of canada balsam and is prevented from emerging from the other face. The extraordinary ray alone is transmitted through the crystal which is plane polarised.

Uses of Nicol prism

• It produces plane polarised light and functions as a polariser

• It can also be used to analyse the plane polarised light i.e used at an analyser.

Drawbacks of Nicol prism

• Its cost is very high due to scarity of large and flawless calcite crystals

• Due to extraordinary ray passing obliquely through it, the emergent ray is always displaced a little to one side.

• The effective field of view is quite limited

• Light emerging out of it is not uniformly plane polarised.

4. Polarisation by scattering

The light from a clear blue portion of the sky shows a rise and fall of intensity when viewed through a polaroid which is rotated. This is because of sunlight, which has changed its direction (having been scattered) on encountering the molecules of the earth’s atmosphere. As Figure 6.81 shows, the incident sunlight is unpolarised. The electric field of light interact with the electrons present in the air molecules.

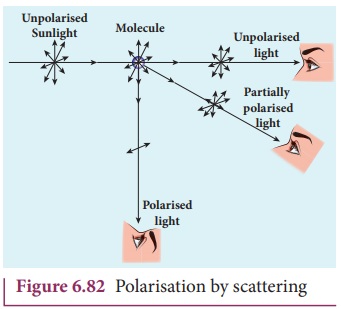
Under the influence of the electric field of the incident wave the electrons in the molecules acquire components of motion in both these directions. We have shown an observer looking at 90° to the direction of the sun. Clearly, charges accelerating parallel do not radiate energy towards this observer since their acceleration has no transverse component. The radiation scattered by the molecule is therefore  polarized perpendicular to the plane of the Figure 6.82. This explains the reason for polarisation of sunlight by scattering.