Chapter: 12th Physics : UNIT 7 : Wave Optics
Diffraction at single slit
Diffraction at single slit
Let a parallel beam of light fall normally on a single slit AB of width a as shown in Figure 6.63. The diffracted beam falls on a screen kept at a distance. The center of the slit is C. A straight line through C perpendicular to the plane of slit meets the center of the screen at O. We would like to find the intensity at any point P on the screen. The lines joining P to the different points on the slit can be treated as parallel lines, making an angle θ with the normal CO.
All the waves start parallel to each other from different points of the slit and interfere at point P and other points to give the resultant intensities. The point P is in the geometrically shadowed region, up to which the central maximum is spread due to diffraction as shown Figure 6.63. We need to give the condition for the point P to be of various minima.
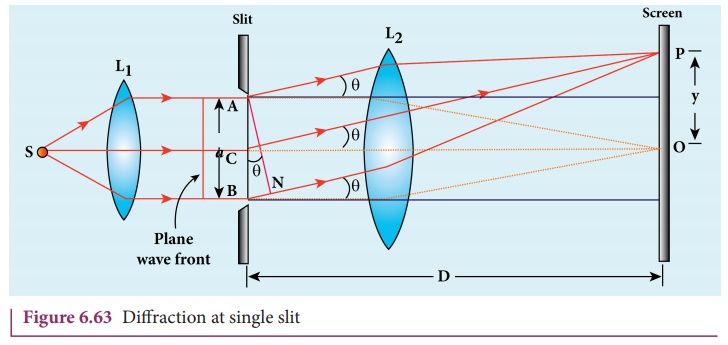
The basic idea is to divide the slit into much smaller even number of parts. Then, add their contributions at P with the proper path difference to show that destructive interference takes place at that point to make it minimum. To explain maximum, the slit is divided into odd number of parts.
Condition for P to be first minimum
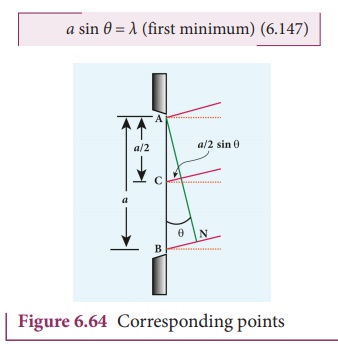
Let us divide the slit AB into two half ’s AC and CB. Now the width of AC is (a/2). We have different points on the slit which are separated by the same width (here a/2) called corresponding points as shown in Figure 6.64.
The path difference of light waves from different corresponding points meeting at point P and interfere destructively to make it first minimum. The path difference δ between waves from these corresponding points is, δ = a/2 sinθ
The condition for P to be first minimum, a/2 sinθ = λ/2
Condition for P to be second minimum
Let us divide the slit AB into four equal parts. Now, the width of each part is a/4. We have several corresponding points on the slit which are separated by the same width a/4. The path difference δ between waves from these corresponding points is, δ = a/4 sinθ.
The condition for P to be second minimum, a/4 sinθ = λ/2
a sin θ = 2λ (second minimum) (6.148)
Condition for P to be third order minimum
The same way the slit is divided in to six equal parts to explain the condition for P to be third minimum is, a/6 sinθ = λ/2
a sin θ = 3λ (third minimum) (6.149)
Condition for P to be nthorder minimum
Dividing the slit into 2n number of (even number of) equal parts makes the light produced by one of the corresponding points to be cancelled by its counterpart. Thus, the condition for nth order minimum is a/2n sinθ = λ/2
a sin θ = nλ (nth minimum) (6.150)
Condition for maxima
For points of maxima, the slit is to be divided in to odd number of equal parts so that one part remains un-cancelled making the point P appear bright.
The condition for first maximum is,
In the same way, condition for nth maximum is,
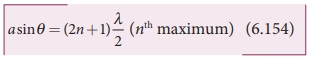
where, n = 0, 1, 2, 3, . . . , is the order of diffraction maximum.
The central maximum is called 0th order maximum. The points of the maximum intensity lie nearly midway between the successive minima.
Here, sinθ gives the angular spread of the diffraction. The position of the minimum or maximum in terms of y may be expressed by replacing sinθ approximated by tanθ, as θ is small, sinθ = tanθ y/D
Where, y is the position of the minimum from the center of the screen and D is the distance between single slit and the screen.
EXAMPLE 6.31
Light of wavelength 500 nm passes through a slit of 0.2 mm wide. The diffraction pattern is formed on a screen 60 cm away. Determine the,
(i) angular spread of central maximum
(ii) the distance between the central maximum and the second minimum.
Solution
λ = 500 nm = 500×10-9 m; a = 0.2 mm = 0.2×10-3 m; D = 60 cm = 60×10-2 m
(i) Equation for diffraction minimum is, a sin θ = nλ
The central maximum is spread up to the first minimum. Hence, n = 1
(ii) To find the value of y1 for central maximum, which is spread up to first minimum with (n = 1) is, a sin θ = λ
To find the value of y2 for second minimum with (n = 2) is, a sin θ = 2λ
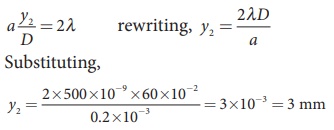
The distance between the central maximum and second minimum is, y2 – y1
y2 – y1 = 3 mm – 1.5 mm = 1.5 mm
Note: The above calculation shows that in the diffraction pattern caused by single slit, the width of each maximum is equal with central maximum as the double that of others. But the bright and dark fringes are not of equal width.
EXAMPLE 6.32
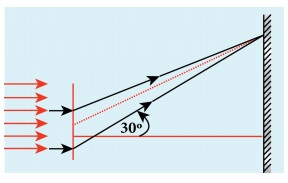
A monochromatic light of wavelength 5000 Ã… passes through a single slit producing diffraction pattern for the central maximum as shown in the figure. Determine the width of the slit.
Solution
λ = 5000 Å = 5000×10-10 m; sin 30º = 0.5; n = 1; a =?
Equation for diffraction minimum is, asin θ = nλ
The central maximum is spread up to the first minimum. Hence, n = 1
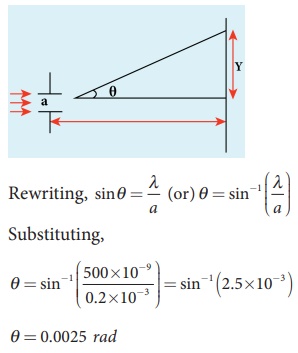
Rewriting, a = λ / Sinθ
Substituting, a = 5000×10−10 / 0.5
a = 1×10−6 m = 0.001×10−3m = 0.001mm
Discussion on first minimum
Let us consider the condition for first minimum with (n = 1). a sin θ = λ
The first minimum has an angular spread of, sinθ = λ/a
Now, we have special cases to discuss on the above condition.
(i) When a < λ, the diffraction is not possible, because sinθ can never be greater than 1.
(ii) When a ≥ λ, the diffraction is possible.
◗ For a = λ, sinθ = 1 i.e, θ = 90º. That means the first minimum is at 90º. Hence, the central maximum spreads fully in to the geometrically shadowed region leading to bending of the diffracted light to 90º.
◗ For a >> λ, sinθ << 1 i.e, the first minimum will fall within the width of the slit itself. The diffraction will not be noticed at all.
(iii) When a > λ and also comparable, say a = 2λ, sinθ = λ/a = λ/2λ = 1/2; then θ = 30º. These are practical cases where diffraction could be observed effectively.
Related Topics