Diffraction in grating

Diffraction in grating

Grating has multiple slits with equal widths of size comparable to the wavelength of diffracting light. Grating is a plane sheet of transparent material on which opaque rulings are made with a fine diamond pointer. The modern commercial grating contains about 6000 lines per centimetre. The rulings act as obstacles having a definite width b and the transparent space between the rulings act as slit of width a. The combined width of a ruling and a slit is called grating element (e = a + b). Points on successive slits separated by a distance equal to the grating element are called corresponding points.

Interference

• Superposition of two waves

• Superposition of waves from two coherent sources.

• Equally spaced fringes.

• Intensity of all the bright fringes is almost same

• Large number of fringes are obtained

Diffraction

• Bending of waves around edges

• Superposition wavefronts emitted from various points of the same wavefront.

• Unequally spaced fringes

• Intensity falls rapidly for higher orders

• Less number of fringes are obtained

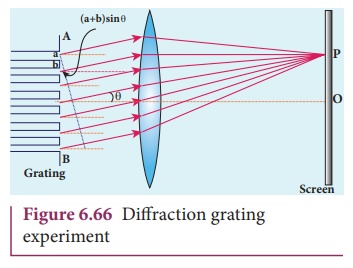
A plane transmission grating is represented by AB in Figure 6.66. Let a plane wavefront of monochromatic light with wave length Î» be incident normally on the grating. As the slits size is comparable to that of wavelength, the incident light diffracts at the grating.

A diffraction pattern is obtained on the screen when the diffracted waves are focused on a screen using a convex lens. Let us consider a point P at an angle Î¸ with the normal drawn from the center of the grating to the screen. The path difference Î´ between the diffracted waves from one pair of corresponding points is,

δ = (a + b) sinθ                (6.156)

This path difference is the same for any pair of corresponding points. The point P will be bright, when

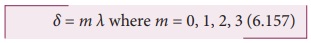
δ = m λ where m = 0, 1, 2, 3             (6.157)

Combining the above two equations, we get,

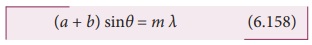
(a + b) sinθ = m λ             (6.158)

Here, m is called order of diffraction.

Condition for zero order maximum, m = 0

For (a + b) sinθ = 0, the position, Î¸ = 0. sinθ = 0 and m = 0. This is called zero order diffraction or central maximum.

Condition for first order maximum, m = 1

If (a + b) sinθ1 = Î», the diffracted light meet at an angle Î¸1 to the incident direction and the first order maximum is obtained.

Condition for second order maximum, m = 2

Similarly, (a + b) sinθ2 = 2λ forms the second order maximum at the angular position Î¸2.

Condition for higher order maximum

On either side of central maxima different higher orders of diffraction maxima are formed at different angular positions.

If we take,

Then, N gives the number of grating elements or rulings drawn per unit width of the grating. Normally, this number N is specified on the grating itself. Now, the equation becomes,

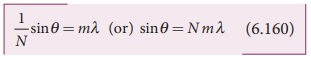
The students should remember that in a single slit experiment the formula, a sinθ = nλ is condition for minimum with n as order of minimum. But, the formula in diffraction grating, sinθ = Nmλ is condition for maxima with m as the order of diffraction.

EXAMPLE 6.34

A diffraction grating consisting of 4000 slits per centimeter is illuminated with a monochromatic light that produces the second order diffraction at an angle of 30°. What is the wavelength of the light used?

Solution

Number of lines per cm = 4000; m = 2;

θ = 30°; Î» = ?

Number of lines per unit length,

N = 4000 / 1×10−2 = 4×105

Equation for diffraction maximum in grating is, sinθ = Nmλ

Rewriting, λ = sinθ / Nm

Substituting,

λ = sin 30º / 4×105×2 =  0.5 / 4×105×2

= 1 / [2×4×105 Ã—2] = 1 / [16×105]

λ = 6250×10−10 m = 6250 Ao

EXAMPLE 6.35

A monochromatic light of wavelength of 500 nm strikes a grating and produces fourth order bright line at an angle of 30°. Find the number of slits per centimeter.

Solution

λ = 500 nm = 500×10-9 m; m = 4;

θ = 30°; number of lines per cm = ?

Equation for diffraction maximum in grating is, sin Î¸ = Nm λ

Rewriting, N = sinθ / mλ

Substituting,

N = 0.5 / 4×500×10−9 = 1 / 2×4×500×10−9

N = 2.5×105 lines per meter

number of lines per centimeter = 2.5×105 Ã—10−2 = 2500 lines per centimetre