The eye

The eye

Eye is a natural optical instrument given by God to the human beings. The internal structure and the Physics aspect of the functioning of different parts of human eye are discussed already in (X Physics Unit-2). As the eye lens is flexible, its focal length can be changed to some extent. When the eye is fully relaxed, the focal length is maximum and when it is strained the focal length is minimum. The image must be formed on the retina for a clear vision. The diameter of eye for a normal adult is about 2.5 cm. Hence, the image-distance, in other words, the distance between eye lens and retina is fixed always at 2.5 cm for a normal eye. 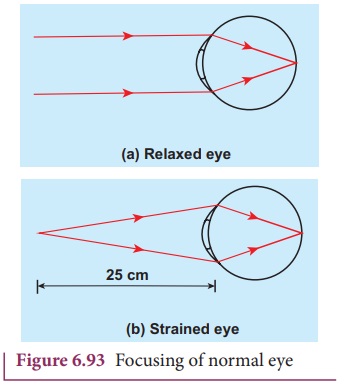We can just discuss the optical functioning of eye without giving importance to the refractive indices of the two liquids, aqueous humor and virtuous humor present in the eye A person with normal vision can see objects kept at infinity in the relaxed condition with maximum focal length f_max of the eye as shown in Figure 6.93(a). Also at a distance of 25 cm in the strained condition  with minimum focal length f_min of the eye as shown in Figure 6.93(b).

Let us find f_max and f_min of human eye from the lens equation given below.

When the object is at infinity, u = –∞, and v = 2.5 cm (distance between eye lens and retina), the eye can see the object in relaxed condition with f_max. Substituting these values in the lens equation gives,

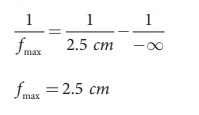
When the object is at near point, u = –25 cm, and v = 2.5 cm, the eye can see the object in strained condition with f_min. Substituting these values in the lens equation gives,

See, the small variation of f_max − f_min = 0.23 cm of the focal length of eye lens makes objects visible from infinity to near point for a normal person. Now, we can discuss some common defects of vision in the eye.

Nearsightedness (myopia)

A person suffering from nearsightedness or myopia cannot see distant objects clearly. This may result because the lens has too short focal length due to thickening of the lens or larger diameter of the eyeball than usual. These people have difficulty in relaxing their eye more than what is needed to overcome this difficulty. Thus, they need correcting lens.

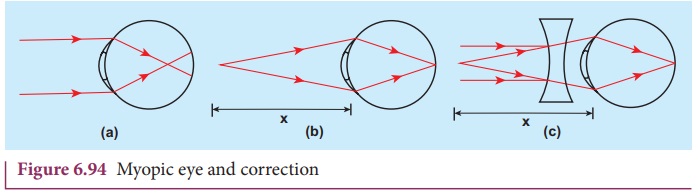
The parallel rays coming from the distant object get focused before reaching the retina as shown in Figure 6.94(a). But, these persons can see objects which are nearer. Let x be the maximum distance up to which a person with nearsightedness can see as shown in Figure 6.94(b). To overcome this difficulty, the virtual image of the object at infinity should be formed at a distance x from the eye using a correcting lens as shown in Figure 6.93(c).

The focal length of the correcting lens for a myopic eye can be calculated using the lens equation.

Here, u = –∞, v = –x. Substituting thes values in the lens equation gives,

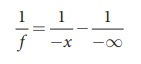
Focal length f of the correcting lens is,

 f = –x            (6.196)

The negative sign in the above result suggests that the lens should be a concave lens. Basically, the concave lens slightly diverges the parallel rays from infinity and makes them focus now at the retina which got earlier focused before reaching retina in the unaided condition.

Farsightedness (hypermetropia)

A person suffering from farsightedness or hypermetropia or hyperopia cannot clearly see objects close to the eye. It occurs when the eye lens has too long focal length due to thining of eye lens or shortening of the eyeball than normal. The least distance for clear vision for these people is appreciably more than 25 cm and the person has to keep the object inconveniently away from the eye. Thus, reading or viewing smaller things held in the hands is difficult for them. This kind of farsightedness arising due to aging is called presbyopia as the aged people cannot strain their eye more to reduce the focal length of the eye lens.

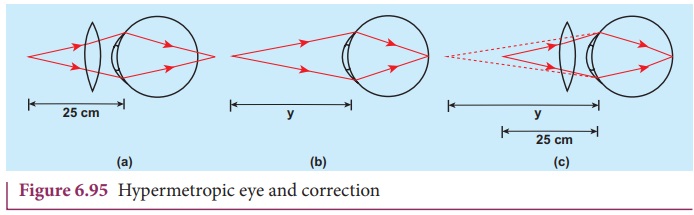
The rays coming from the object at near point get focused beyond the retina as shown in Figure 6.95(a). But, these persons can see objects which are far say, more than 25 cm. Let y be the minimum distance from the eye beyond which a person with farsightedness can see as shown in Figure 6.95(b). To overcome this difficulty, the virtual image of the object at y should be formed at a distance of 25 cm (near point) from the eye using a correcting lens as shown in Figure 6.95(c).

The focal length of the correcting lens for a hypermetropic eye can be calculated using the lens equation.

Here, u = –y, v = –25 cm. Substituting these values in the lens equation gives,

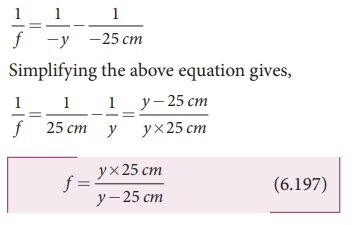
The focal length calculated using above formula will be positive as y is always greater than 25 cm. The positive sign of the focal length suggests that the lens should be a convex lens. In principle, the convex lens slightly converges the rays coming from beyond y and makes them focus now at the retina which got earlier focused beyond retina for the unaided eye.

Astigmatism

Astigmatism is the defect arising due to different curvatures along different planes in the eye lens. Astigmatic person cannot see all the directions equally well. The defect due to astigmatism is more serious than myopia and hyperopia. The remedy to astigmatism is using of lenses with different curvatures in different planes to rectify the defect. In general, these specially made glasses with different curvature for different planes are called as cylindrical lenses.

Due to aging people may develop combination of more than one defect. If it is the combination of nearsightedness and farsightedness then, such persons may need a converging glass for reading purpose and a diverging glass for seeing at a distance. Bifocal lenses and progressive lenses provide solution for these problems.

EXAMPLE 6.44

Calculate the power of the lens of the spectacles necessary to rectify the defect of nearsightedness for a person who could see clearly only up to a distance of 1.8 m.

Solution

The maximum distance the person could see is, x = 1.8 m.

The lens should have a focal length of, f = –x m = –1.8 m.

It is a concave or diverging lens.

The power of the lens is,

P = − 1/1.8 m

= −0.56 diopter

EXAMPLE 6.45

A person has farsightedness with the minimum distance he could see clearly is 75 cm. Calculate the power of the lens of the spectacles necessary to rectify the defect.

Solution

The minimum distance the person could see clearly is, y = 75 cm.

The lens should have a focal length of,

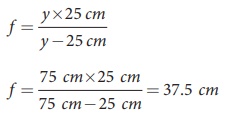
f = y×25 cm / y-25 cm

f = [75 cm×25 cm ] / [75 cm −25 cm] = 37.5 cm

It is a convex or converging lens.

The power of the lens is,

P = 1 / 0.375 m  = 2.67 diopter