Near point focusing, Normal focusing | Optical Instruments - Simple microscope | 12th Physics : UNIT 7 : Wave Optics
Chapter: 12th Physics : UNIT 7 : Wave Optics
Simple microscope
Simple microscope
A simple microscope is a single
magnifying (converging) lens of small focal length. The idea is to get an
erect, magnified and virtual image of the object. For this the object is placed
between F and P on one side of the lens and viewed from other side of the lens.
There are two magnifications to be discussed for two kinds of focussing.
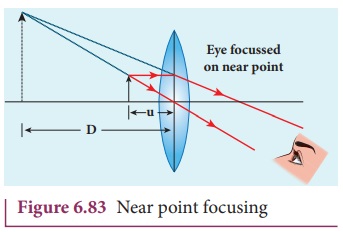
(1) Near point focusing ŌĆō The image is formed at near point, i.e. 25
cm for normal eye. This distance is also called as least distance D of distinct vision. In this position, the eye
feels comfortable but there is little strain on the eye. This is shown in
Figure 6.83
(2) Normal focusing ŌĆō The image is formed at infinity. In this position
the eye is most relaxed to view the image. This is shown in Figure 6.84(b).
Magnification in near point focusing
The near point focusing is shown in
Figure 6.83. Object distance u is
less than f. The image distance is
the near point D. The magnification m
is given by the relation,

With the help of lens equation, 1/v ŌĆō 1/u = 1/f the magnification can further be written as,

Substituting for v with sign convention, v = ŌĆōD

This is the magnification for near
point focusing.
Magnification in normal focusing (angular magnification)
The normal focusing is shown in
Figure 6.84(b). We will now find the magnification for the image formed at
infinity. If we take the ratio of height of image to height of object (m=hŌĆÖ/h) to find the magnification, we will
not get a practical relation, as the image will also be of infinite size when
the image is formed at infinity. Hence, we can practically use the angular
magnification. The angular magnification is defined as the ratio of angle ╬Ėi
subtended by the image with aided eye to the angle ╬Ė0 subtended by the object with unaided eye.
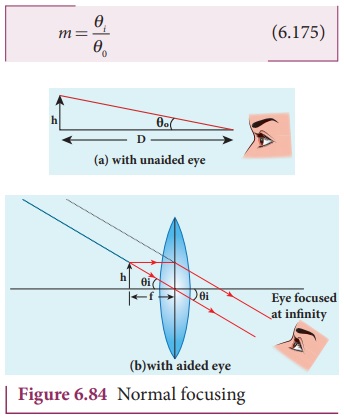
For unaided eye shown in Figure
6.84(a),

This is the magnification for normal
focusing.
The magnification for normal
focusing is one less than that for near point focusing. But, the viewing is
more comfortable in normal focusing than near point focusing. For large values of
D/f,
the difference in magnification is usually small. In subsequent discussions, we
shall only consider the normal focusing.
EXAMPLE 6.41
A man with a near point of 25 cm
reads a book with small print using a magnifying glass, a convex lens of focal
length 5 cm. (a) What is the closest and the farthest distance at which he
should keep the lens from the page so that he can read the book when viewing
through the magnifying glass? (b) What is the maximum and the minimum angular
magnification (magnifying power) possible using the above simple microscope?
Solution
D = 25 cm; f = 5 cm;
For closest object distance, u; the image distance, v is, ŌĆō25 cm. (near point focusing)
For farthest object distance, uŌĆÖ; the corresponding image distance, vŌĆÖ is, vŌĆÖ = Ōł× (normal focusing)
(a) To find closest image distance,
lens equation, 1/v ŌĆō 1/u = 1/f
Rewriting for closest object distance, 1/u = 1/v - 1/f
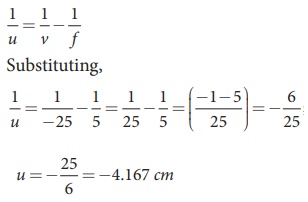
The closest distance at which the
person should can keep the book is, u =
ŌĆō4.167 cm
To find farthest object distance, lens
equation is, 1/vŌĆÖ ŌĆō 1/uŌĆÖ = 1/fŌĆÖ
Rewriting for farthest object
distance, 1/uŌĆÖ = 1/vŌĆÖ - 1/fŌĆÖ
Substituting, 1/uŌĆÖ = 1/Ōł× - 1/5; u
= ŌłÆ5 cm
The farthest distance at which the
person can keep the book is, uŌĆ▓ = ŌłÆ5 cm
(b) To find magnification in near
point
focusing, m =
1+ D/f = 1+ 25/5 = 6
To find magnification in normal
focusing,
m = D/f = 25/5 = 5
Resolving power of microscope
The diagram related to the calculation of resolution of
microscope is illustrated in Figure 6.85. A microscope is used to see the
details of the object under observation. The ability of microscope depends not
only in magnifying the object but also in resolving two points on the object
separated by a small distance dmin.
Smaller the value of dmin better
will be the resolving power of the microscope.
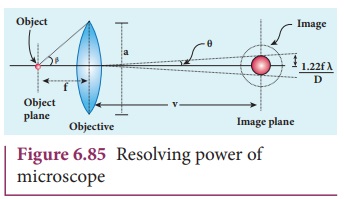
The radius of central maxima is already derived as equation
6.159,

In the place of focal length f
we have the image distance v. If
the difference between the two points on the object to be resolved is dmin, then the magnification m is,

To further reduce the value of dmin the optical path of the light is increased by
immersing the objective of the microscope in to a bath containing oil of
refractive index n.

Such an objective is called oil immersed objective. The term nsin╬▓ is called numerical
aperture NA.
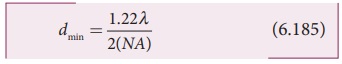
Related Topics