Interference with polychromatic light and in thin films

Interference with polychromatic light

When a polychromatic light (white light) is used in interference experiment, coloured fringes of varied thickness will be formed on the screen. This is because, different colours have different wavelengths. However, the central fringe or 0th fringe will always be bright and white in colour, because for all the colours falling at the point O will have no path difference. Hence, only constructive interference is possible at O for all the colours.

EXAMPLE 6.29

Two lights of wavelengths 560 nm and 420 nm are used in Young’s double slit experiment. Find the least distance from the central fringe where the bright fringe of the two wavelengths coincides. Given D = 1 m and d = 3 mm.

Solution

λ = 560 nm = 560×10−9 m;

λ2 = 420 nm = 420×10−9 m;

D = 1 m;d = 3 mm = 3×10−3 m

For a given y, n and Î» are inversely proportional.

Let nth order bright fringe of Î»1 coincides with (n+1)th order bright fringe of Î»2.

Thus, the 3rd bright fringe of Î»1 and 4th bright fringe of Î»2 coincide at the least distance y.

The least distance from the central fringe where the bright fringes of the two wavelengths coincides is, yn = n [(λD)/d]

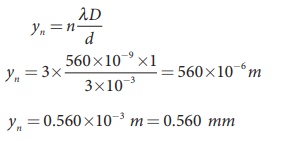
Dazzling colours are exhibited by thin films of oil spread on the surface of water and also by soap bubbles as shown in the figure. These colours are due to interference of white light undergoing multiple reflections from the top and the bottom surfaces of thin films. The colour depends upon the thickness of the film, refractive index of the film and also the angle of incidence of the light.

Interference in thin films

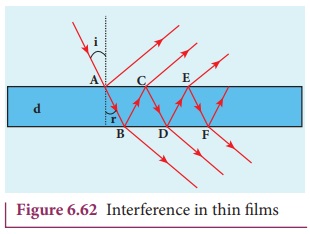
Let us consider a thin film of transparent material of refractive index Âµ (not to confuse with order of fringe n) and thickness d. A parallel beam of light is incident on the film at an angle i as shown in Figure 6.62. The wave is divided into two parts at the upper surface, one is reflected and the other is refracted. The refracted part, which enters into the film, again gets divided at the lower surface into two parts; one is transmitted out of the film and the other is reflected back in to the film. Reflected as well as refracted waves are sent by the film as multiple reflections take place inside the film. The interference is produced by both the reflected and transmitted light.

For transmitted light

The light transmitted may interfere to produce a resultant intensity. Let us consider the path difference between the two light waves transmitted from B and D. The two waves moved together and remained in phase up to B where splitting occurred. The extra path travelled by the wave transmitted from D is the path inside the film, BC + CD. If we approximate the incidence to be nearly normal (i = 0), then the points B and D are very close to each other. The extra distance travelled by the wave is approximately twice thickness of the film, BC + CD = 2d. As this extra path is traversed in a medium of refractive index Âµ, the optical path difference is, Î´ = 2µd.

The condition for constructive interference in transmitted ray is,

Similarly, the condition for destructive interference in transmitted ray is,

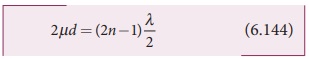
For reflected light

It is experimentally and theoretically proved that a wave while travelling in a rarer medium and getting reflected by a denser medium, undergoes a phase change of Ï€. Hence, an additional path difference of Î»/2 should be considered.

Let us consider the path difference between the light waves reflected by the upper surface at A and the other wave coming out at C after passing through the film. The additional path travelled by wave coming out from C is the path inside the film, AB + BC. For nearly normal incidence this distance could be approximated as, AB + BC = 2d. As this extra path is travelled in the medium of refractive index Âµ, the optical path difference is, Î´ = 2µd.

The condition for constructive interference for reflected ray is,

The additional path difference Î»/2 is due to the phase change of Ï€ in rarer to denser reflection taking place at A.

The condition for destructive interference for reflected ray is,

If the incidence is not nearly normal, but at an angle of incidence i which has an angle of refraction r, then the expression for path difference 2µd on the left hand side of the above equations are to be replaced with the expression, 2µd cos r.

EXAMPLE 6.30

Find the minimum thickness of a film of refractive index 1.25, which will strongly reflect the light of wavelength 589 nm. Also find the minimum thickness of the film to be anti-reflecting.

Solution

λ = 589 nm = 589×10−9 m

For the film to have strong reflection, the reflected waves should interfere constructively. The least optical path difference introduced by the film should be Î»/2. The optical path difference between the waves reflected from the two surfaces of the film is 2µd. Thus, for strong reflection, 2µd = Î»/2 [As given in equation 6.145. with n = 1]

Rewriting, d = λ/4μ

Substituting, d = [589×109] / [4×1.25] = 117.8×10−9

d = 117.8×10−9 = 117.8 nm

For the film to be anti-reflecting, the reflected rays should interfere destructively. The least optical path difference introduced by the film should be Î». The optical path difference between the waves reflected from the two surfaces of the film is 2µd. For strong reflection, 2µd = Î» [As given in equation 6.146. with n = 1].

Rewriting, d = Î»/2μ

Substituting, d = [589×109] / [2×1.25] = 235.6×10−9

d = 235.6×10−9 = 235.6 nm