Velocity of Rectilinear motion - The concept of derivative

The concept of derivative

Calculus grew out of four major problems that mathematicians were working on during the seventeenth century.

1) The tangent line problem

2) The velocity and acceleration problem

3) The minimum and maximum problem

4) The area problem

Velocity of Rectilinear motion

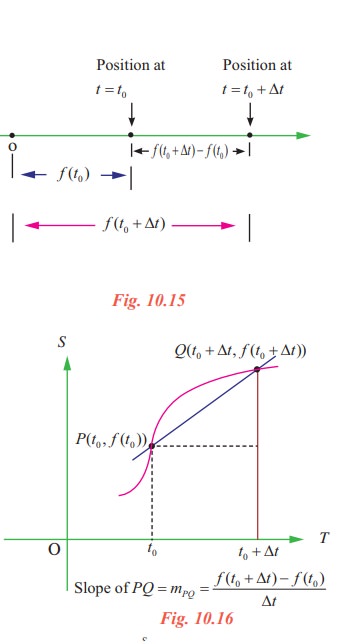
Suppose an object moves along a straight line according to an equation of motion s = f(t), where s is the displacement (directed distance) of the object from the origin at time t. The function f that describes the motion is called the position function of the object. In the time interval from t = t0 to t = t0 + ∆t, the change in position is f(t0 + ∆t) - f(t0). The average velocity over this time interval is

which is same as the slope of the secant line PQ in fig. 10.16.

In this time interval ∆t (from t0 to t0 + ∆t) the motion may be of entirely different types for the same distance covered (traversed). This is illustrated graphically by the fact that we can draw entirely different curves C1, C2, C3 ... between the points P and Q in the plane. These curves are the graphs of quite different motions in the given time intervals, all the motions having the same average velocity ∆s/∆t.

Now suppose we compute the average velocities over shorter and shorter time intervals [t0, t0 + ∆t]. In other words, we let ∆t approach 0. Then we define the velocity (or instantaneous velocity) v(t0) at time t = t0 as the limit of these average velocities.

This means that the velocity at time t = t0 is equal to the slope of the tangent line at P.

Illustration 10.2

The distance s travelled by a body falling freely in a vacuum and the time t of descent are variables. They depend on each other. This dependence is expressed by the law of the free fall:

s= 1/2 gt2  (absence of initial velocity), g is the gravitational constant.

It is clear from this that the velocity is completely defined by the instant t0. It is proportional to the time of motion (of the fall).