Implicit Differentiation

Implicit Differentiation

A function in which the dependent variable is expressed solely in terms of the independent variable x, namely, y = f(x), is said to be an explicit function. For instance, y = ½[ x3 −1] is an explicit function, whereas an equivalent equation 2 y − x3 + 2 = 0 is said to define the function implicitly or y is an implicit function of x.

Now, as we know, the equation

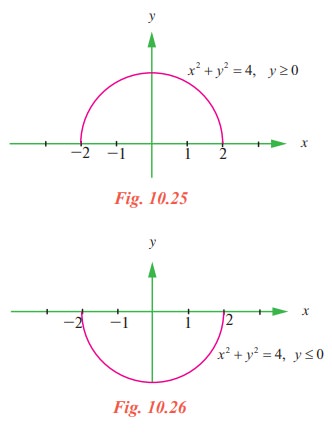
x 2 + y2  = 4 (1)

describes a a circle of radius 2 centered at the origin. Equation (1) is not a function since for any choice of x in the interval - 2 < x < 2 there correspond two values of y, namely

(2) represents the top half of the circle (1) and (3) represents the bottom half of the circle (1). By considering either the top half or bottom half, of the circle, we obtain a function. We say that (1) defines at least two implicit functions of x on the interval - 2 ≤ x ≤ 2.

Note that both equations

x2 + [ f (x)]2 = 4 and x2 + [ g(x)]2 = 4 are identities on the interval −2 ≤ x ≤ 2 .

In general, if an equation  F (x, y) = 0 defines a function f implicitly on some interval, then F (x, f (x)) = 0 is an identity on the interval. The graph of f is a portion (or all) of the graph of the equation F (x, y) = 0 .

A more complicated equation such as x4 + x2 y3 − y5 = 2x +1 may determine several implicit functions on a suitably restricted interval of the x-axis and yet it may not be possible to solve for y in terms of x. However, in some cases we can determine the derivative dy/dx by a process known as implicit differentiation. This process consists of differentiating both sides of an equation with respect to x, using the rules of differentiation and then solving for dy/dx . Since we think of y as being determined by the given equation as a differentiable function, the chain rule, in the form of the power rule for functions, gives the result.