The tangent line problem - The concept of derivative

The tangent line problem

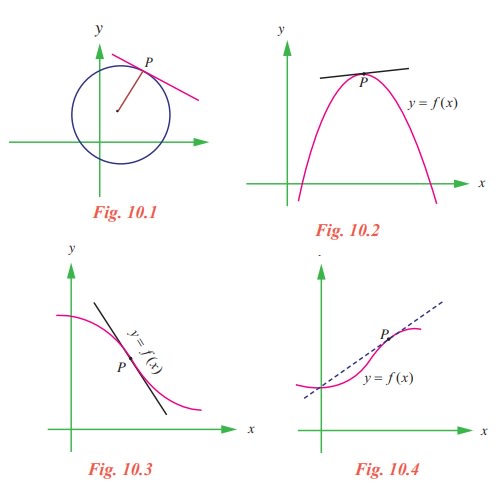
What does it mean to say that a line is tangent to a curve at a point? For a circle, the tangent line at a point P is the line that is perpendicular to the radial line at a point P, as shown in fig. 10.1.

For a general curve, however, the problem is more difficult, for example, how would you define the tangent lines shown in the following figures 10.2 to 10.4.

You might say that a line is tangent to a curve at a point P if it touches, but does not cross, the curve at point P. This definition would work for the first curve (Fig. 10.2), but not for the second (Fig. 10.3). Or you might say that a line is tangent to a curve if the line touches or intersects the curve exactly at one point. This definition would work for a circle but not for more general curves, as the third curve shows (Fig. 10.4).

Essentially, the problem of finding the tangent line at a point P boils down to the problem of finding the slope of the tangent line at point P. You can approximate this slope using a secant line through the point of tangency and a second point on the curve as in the following Fig. 10.5.

Let P(x0, f(x0)) be the point of tangency and Q(x0 + ∆x, f(x0 + ∆x)) be the second point.

The slope of the secant line through the two points is given by substitution into the slope formula

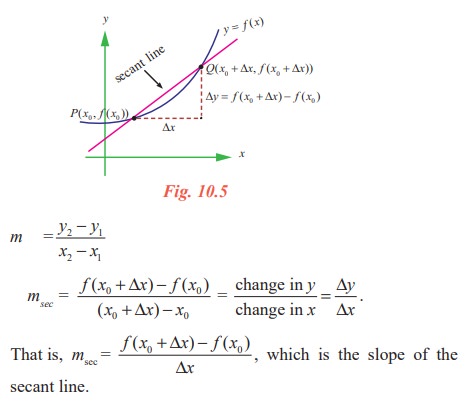
The right hand side of this equation is a difference quotient. The denominator ∆x is the change in x (increment in x), and the numerator ∆y = f(x0 + ∆x) - f(x0) is the change in y.

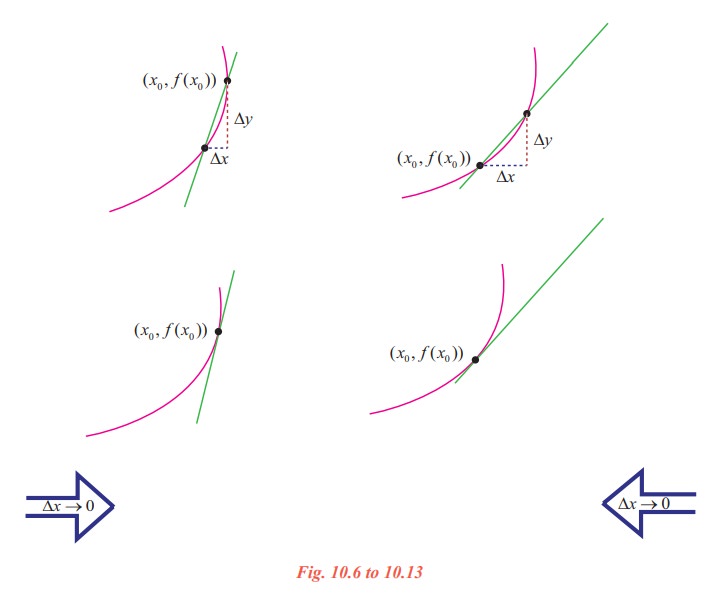
The beauty of this procedure is that you can obtain more and more accurate approximations of the slope of the tangent line by choosing points closer and closer to the point of tangency.

Tangent line approximation

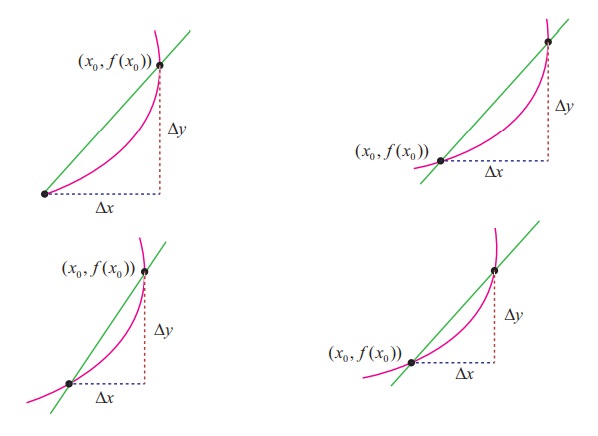
Illustration 10.1

Let us make an attempt to find the slope of the tangent line to the graph of f ( x) = x2at (1, 1). As a start, let us take ∆x = 0.1 and find the slope of the secant line through (1,1) and (1.1, (1.1)2 ).

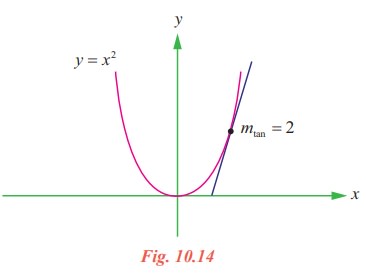
(i) f(1.1) = (1.1)2  = 1.21

(ii) ∆y = f(1.1) - f(1) = 1.21 - 1 = 0.21

(iii) ∆y/∆x = 0.21 / 0.1 = 2.1

Tabulate the successive values to the right and left of 1 as follows :

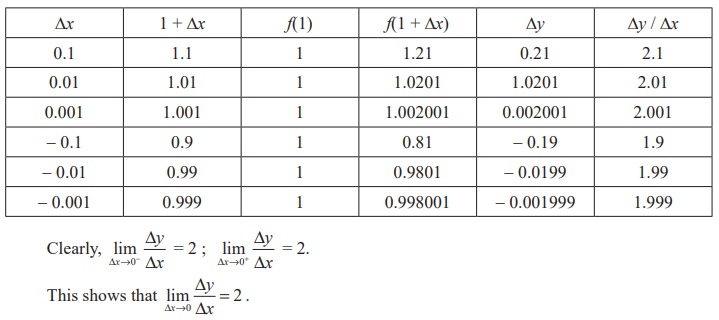
Thus the slope of the tangent line to the graph of y = x2 at (1, 1) is mtan = 2.

On the basis of the Fig.10.6 to 10.13, Illustration 10.1, and our intuition, we are prompted to say that if a graph of a function y = f(x) has a tangent line L at a point P, then L must be the line that is the limit of the secants PQ through P and Q as Q → P (∆x → 0). Moreover, the slope mtan of L should be the limiting value of the values msec as ∆x → 0. This is summarised as follows:

Definition 10.1 (Tangent line with slope m)

Let f be defined on an open interval containing x0, and if the limit

exists, then the line passing through (x0, f(x0)) with slope m is the tangent line to the graph of f at the point (x0, f(x0)).

The slope of the tangent line at (x0, f(x0)) is also called the slope of the curve at that point.

The definition implies that if a graph admits tangent line at a point (x0, f(x0)) then it is unique since a point and a slope determine a single line.

The conditions of the definition can be formulated in 4 steps :

(i) Evaluate f at x0 and x0 + ∆x : f(x0) and f(x0 + ∆x)

(ii) Compute ∆y : ∆y = f(x0 + ∆x) - f(x0)

(iii) Divide ∆y by ∆x (≠ 0) :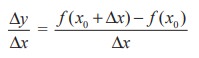

(iv) Compute the limit as ∆x→0 : mtan =

The computation of the slope of the graph in the Illustration 10.1 can be facilitated using the definitions.

(i) f(1) = 12 = 1. For any ∆x ≠ 0

f(1 + ∆x) = (1 + ∆x)2 = 1 + 2∆x + (∆x)2

(ii) ∆y = f(1 + ∆x) - f(1) = 2∆x + (∆x)2 = ∆x (2 + ∆x)

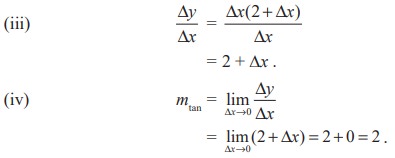
Example 10.1

Find the slope of the tangent line to the graph of f(x) = 7x + 5 at any point (x0, f(x0)).

Solution

Step (i) f(x0) = 7x0 + 5.

For any ∆x≠0 ,

f(x0 + ∆x) = 7(x0 + ∆x) + 5

= 7x0 + 7∆x + 5

Step (ii)

∆y = f(x0 + ∆x) - f(x0)

= (7x0 + 7∆x + 5) − (7x0 + 5)

= 7∆x

Step (iii)

∆y/∆x = 7

Thus, at any point on the graph of f(x) = 7x + 5, we have

Step (iv)

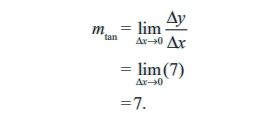
= 7.

Note that for a linear graph, ∆y/∆x  is a constant, depends neither on x0 nor on the increment ∆x.

Example 10.2

Find the slope of tangent line to the graph of f(x) = - 5x2 + 7x at (5, f(5)).

Solution

Step (i)

f(5) = - 5(5)2 + 7 × 5 = - 125 + 35 = - 90.

For any  ∆x≠ 0 ,

f(5 + ∆x) = - 5(5 + ∆x)2 + 7(5 + ∆x) = - 90 - 43∆x - 5(∆x)2.

Step (ii)

∆y = f(5 + ∆x) - f(5)

= - 90 - 43∆x - 5(∆x)2 + 90 = - 43∆x - 5(∆x)2

=  ∆x [- 43 - 5∆x].

Step (iii)

∆y/∆x = - 43 - 5∆x

Step (iv)