Chapter: 11th Mathematics : UNIT 10 : Differential Calculus: Differentiability and Methods of Differentiation
Differential Calculus- Differentiability and Methods of Differentiation
Differential Calculus- Differentiability and Methods of Differentiation
Introduction
In this chapter we discuss the concept of derivative and related concepts and develop tools necessary for solving real life problems. In this connection, let us look at the following problem of finding average velocity.
Almost everyone has an intuitive notion of speed or velocity as a rate at which a distance is covered in a certain length of time. When, say, a bus travels 60 km in one hour, the average velocity of the bus must have been 60 km/h. Of course, it is difficult to maintain this rate of 60 km/h for the entire trip because the bus slows down for towns and speeds up when it passes cars. In other words, the velocity changes with time. If a bus company’s schedule demands that the bus travel 60 km from one town to another in one hour, the driver knows instinctively that he must compensate for velocities or speeds greater than this at other points in the journey. Knowing that the average velocity is 60 km/h does not, however, answer the question: What is the velocity of the bus at a particular instant?

In general, this average velocity or average speed of a moving object is the time rate of change of position defined by
Vave = distance travelled / time of travel
Consider a runner who finishes a 10 km race in an elapsed time of 1 h 15 min (1.25 h). The runner’s average velocity or average speed for this race is
vave = 10/1.25 = 8
But suppose we now wish to determine the runner’s exact velocity v at the instant the runner is one-half into the race. If the distance run in the time interval from 0 h to 0.5 h is measured to be 5 km, then v = 5/0.5 = 10 .
Again this number is not a measure or necessarily such a good indicator, of the instantaneous rate v at which the runner is moving 0.5 h into the race. If we determine that rate at 0.6 h the runner is 5.7 km from the starting line, then the average velocity from 0 h to 0.6 h is
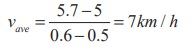
The latter number is a more realistic measure of the rate v. By “shrinking” the time interval between 0.5 h and the time that corresponds to a measured position close to 5 km, we expect to obtain even better approximations to the runner’s velocity at time 0.5 h.

This problem of finding velocities leads us to deal with the general problem of finding the derivative of a general mathematical model represented by the analytic equation, y = f ( x ) Consequently, we will move towards in achieving the following objectives and subsequently deal with the analysis of derivatives.
Related Topics