One sided derivatives (left hand and right hand derivatives) - The concept of derivative

One sided derivatives (left hand and right hand derivatives)

For a function y = f(x) defined in an open interval (a, b) containing the point x0, the left hand and right hand derivatives of f at x = x0 are respectively denoted by f ′(x0− ) and f ′(x0+ ), are defined as

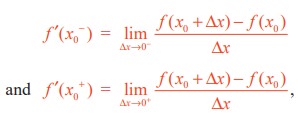, provided the limits exist.

That is, the function is differentiable from the left and right. As in the case of the existence of limits of a function at x0 , it follows that

Definition 10.3

A function f is said to be differentiable in the closed interval [ a , b] if it is differentiable on the open interval ( a , b) and at the end points a and b,

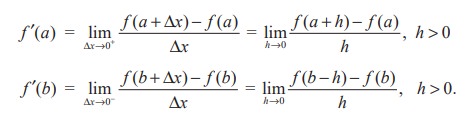
If f is differentiable at x = x0 , then 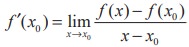, where x = x0 + ∆x and ∆x → 0 is equivalent to x → x0 . This alternative form is some times more convenient to be used in computations.

As a matter of convenience, if we let h = ∆x, then 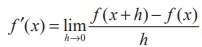, provided the limit exists.