Chapter: 11th Mathematics : UNIT 10 : Differential Calculus: Differentiability and Methods of Differentiation
Differentiation Rules
Differentiation Rules
If f is a real valued function of a real variable defined on an open interval I and if y = f(x) is a differentiable function of x, then
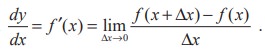
In general finding such direct derivatives using first principle is extremely laborious and difficult operation in the majority of cases. But if we know, once and for all, the derivatives of all the basic elementary functions, together with rules of differentiating the algebra of functions and functions of a function, we can find the derivative of any element – any function without carrying out limit process each time. Hence the operation of differentiation can be made automatic for the class of functions that concern us.
Now we divert our attention to the rules for differentiation of a sum, product and quotient.
Theorem 10.2
The derivative of the sum of two (or more) differentiable functions is equal to the sum of their derivatives. That is, if u and v are two differentiable functions then
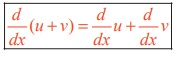
Proof
Let u and v be two real valued functions defined and differentiable on an open interval I ⊆ R.
Let y = u + v, then y = f(x) is a function defined on I, and by hypothesis

This can be extended to finite number of differentiable functions u1 ,u2 , ..., un and (u1+ u2+... un) = u1’+ u2’+... un’
Theorem 10.3
Let u and v be two differentiable functions. Then 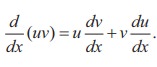
Proof
Let u and v be the given two differentiable functions so that

Similarly (uvw)′ = uvw′ + uv ′w + u ′vw .
This can be extended to a finite number of differentiable functions u1, u2, ... un, using induction :
(u1 .u 2 ..., u n )’ = u1u 2...u n −1u’n + u1u 2...u’n −1u n + + u’1u 2 un .
Theorem 10.4 (Quotient Rule)
Let u and v be two differentiable functions with v(x) ≠ 0. Then 
Proof
Let y = f (x) = u/v , u and v are differentiable functions of x and where v ( x) ≠ 0 .

Theorem 10.5 (Chain Rule / Composite Function Rule or Function of a Function Rule)
Let y = f(u) be a function of u and in turn let u = g(x) be a function of x so that y = f ( g ( x ) ) = ( fog )( x ).
Then 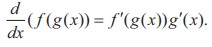
Proof
In the above function u = g(x) is known as the inner function and f is known as the outer function.
Note that, ultimately, y is a function of x.
Now ∆u = g(x + ∆x ) − g(x)

Thus, to differentiate a function of a function y = f ( g (x)) , we have to take the derivative of the outer function f regarding the argument g(x) = u, and multiply the derivative of the inner function g(x) with respect to the independent variable x. The variable u is known as intermediate argument.
Theorem 10.6
Let f(x) be a differentiable function and let y=k f ( x), k≠0. Then 
Proof

Related Topics