Differentiability and Continuity

Differentiability and Continuity

Illustration 10.3

Test the differentiability of the function f(x) = |x - 2| at x = 2.

Solution

We know that this function is continuous at x = 2.

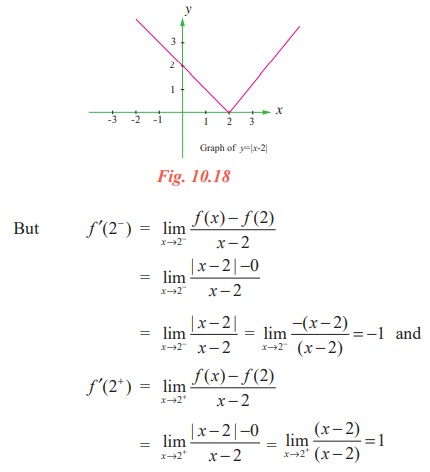
Since the one sided derivatives f ′(2− ) and f ′(2+ ) are not equal, f ′ (2) does not exist. That is, f is not differentiable at x = 2. At all other points, the function is differentiable.

If x0 ≠ 2 is any other point then

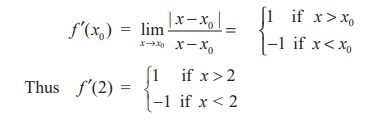
The fact that f ′ (2) does not exist is reflected geometrically in the fact that the curve y = |x - 2| does not have a tangent line at (2, 0). Note that the curve has a sharp edge at (2, 0).

Illustration 10.4

Examine the differentiability of f (x ) = x1/3 at x = 0.

Solution

Let f (x ) = x1/3. Clearly, there is no hole (or break) in the graph of this function and hence it is continuous at all points of its domain.

Let us check whether f ′(0) exists.

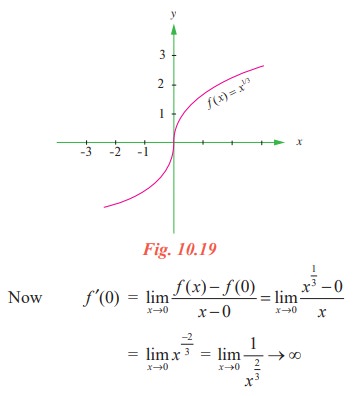
Therefore, the function is not differentiable at x = 0. From the Fig. 10.19, further we conclude that the tangent line is vertical at x = 0. So f is not differentiable at x = 0.

If a function is continuous at a point, then it is not necessary that the function is differentiable at that point.

What can you say about the differentiability of this function at other points?

Illustration 10.5

Therefore f ′ (0) does not exist.

Here we observe that the graph of f has a jump at x = 0. That is x = 0 is a jump discontinuity.

The above illustrations and examples can be summarised to have the following conclusions.

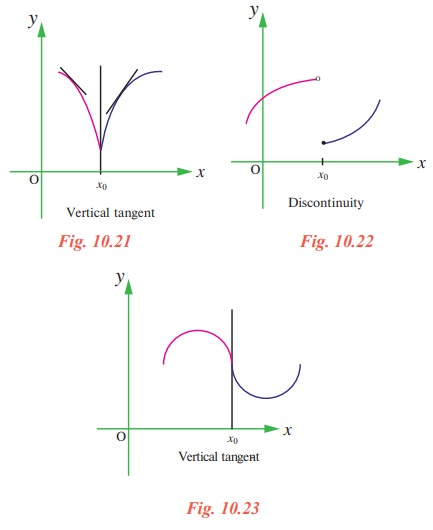
A function f is not differentiable at a point x0 belonging to the domain of f if one of the following situations holds:

(i) f has a vertical tangent at x0.

(ii)The graph of f comes to a point at x0 (either a sharp edge ∨ or a sharp peak ∧ )

(iii) f is discontinuous at x0.

A function fails to be differentiable under the following situations :

We have seen in illustration 10.3 and 10.4, the function f(x) = |x-2| and f(x) = x1/3 are respectively continuous at x = 2 and x = 0 but not differentiable there, whereas in Example 10.3 and Illustration 10.5, the functions 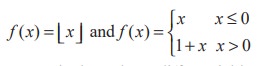are respectively not continuous at any integer x = n and x = 0 respectively and not differentiable too. The above argument can be condensed and encapsuled to state: Discontinuity implies non-differentiability.

Theorem 10.1 (Differentiability implies continuity)

If f is differentiable at a point x = x0, then f is continuous at x0.

Proof

Let f(x) be a differentiable function on an interval (a, b) containing the point x0. Then

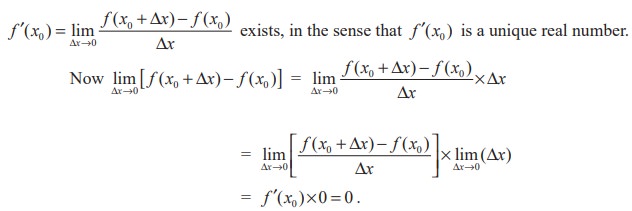
This implies, f is continuous at x = x0.

Derivatives from first principle

The process of finding the derivative of a function using the conditions stated in the definition of derivatives is known as derivatives from first principle.

EXERCISE 10.1

(1) Find the derivatives of the following functions using first principle.

(i) f (x) = 6 (ii) f(x) = - 4x + 7 (iii) f(x) = - x2 + 2

(2) Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?

(3) Determine whether the following function is differentiable at the indicated values.

(i) f(x) = x | x | at x = 0

(ii) f(x) = | x 2 - 1 | at x =1

(iii) f(x) = |x| + |x - 1| at x = 0, 1

(iv) f (x ) = sin | x | at x = 0

(4) Show that the following functions are not differentiable at the indicated value of x.

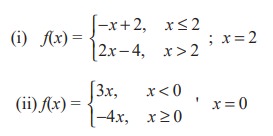
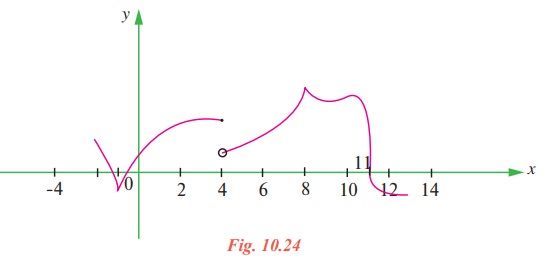
(5) The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.

(6) If f(x) = |x + 100| + x2, test whether f ′(−100) exists.

(7) Examine the differentiability of functions in  R by drawing the diagrams.

(i) | sin x |  (ii) | cos x | .