Chapter: 11th Mathematics : UNIT 10 : Differential Calculus: Differentiability and Methods of Differentiation
Derivatives of basic elementary functions - Differentiation Rules
Derivatives of basic elementary functions
We shall now find the derivatives of all the basic elementary functions; we start with the constant function.
(1) The derivative of a constant function is zero.
Let y = f(x) = k, k is a constant.
Then f(x +∆x) = k and
f(x + ∆x) - f(x) = k - k = 0.

(2) The power function y = xn, n > 0 is an integer.
Let f(x) = xn.
Then, f(x+ ∆x) = (x + ∆x)n and
f(x + ∆x) - f(x) = (x + ∆x)n - xn.

(3) Derivative of the logarithmic function
The natural logarithm of x is denoted by loge x or logx or ln x
Let y = f (x) = log x
Now f (x + ∆x) = log (x + ∆x) and
f(x + ∆x) - f(x) = log (x + ∆x) - log x

(4) Derivative of the exponential function
Let y = ax
Then f (x + ∆x) - f (x) = ax +Δx− ax
= ax (a ∆x−1) and

(5) The derivatives of the Trigonometric functions
(i) The sine function, sinx.
Let y = f (x ) = sin x .
Then f (x + ∆x) = sin(x + ∆x) and

(ii) The cosine function, cos x

(iii) The tangent function, tan x
Let y = f (x) = tan x .

(iv) The secant function, sec x

(v) The cosecant function, cosec x
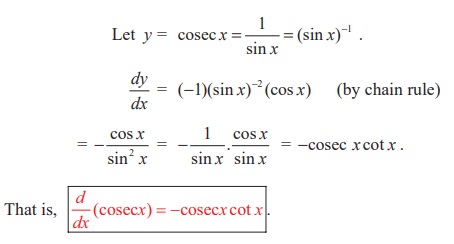
(vi) The cotangent function, cot x

(6) The derivatives of the inverse trigonometric functions
(i) The derivative of arcsin x or sin−1 x
Let y= f (x) = sin−1 x .
Then y + ∆y= f (x + ∆x ) = sin−1 (x + ∆x)
This implies, x= sin y and
x + ∆x= sin (y + ∆y).

(ii) The derivative of arccos x or cos−1x
We know the identity :

(iii) The derivative of arctan x or tan−1 x
Let y = f (x ) = tan−1 x . ... (1)
This implies, y + ∆y= f(x + ∆x) = tan−1 (x + ∆x) ... (2)
x= tan y and
x+ ∆x = tan (y + ∆y)
This implies, ∆x = tan (y + ∆y) - tan y

(iv) The derivative of arccot x or cot−1 x

(v) The derivative of arcsec x or
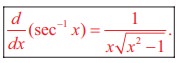
(vi) The derivative of arccosec x or
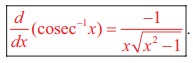
The proofs of (v) and (vi) are left as exercises.

EXERCISE 10.2
Find the derivatives of the following functions with respect to corresponding independent variables:
(1) f(x) = x - 3 sinx
(2) y = sin x + cos x
(3) f(x) = x sin x
(4) y = cos x - 2 tan x
(5) g(t) = t3cos t
(6) g(t) = 4 sec t + tan t
(7) y = ex sin x
(8) y = tanx /x
(9) y = sin x / [1+ cos x]
(10) y = x / [sin x + cos x]
(11) y = tan x −1 / sec x
(12) y = sin x / x2
(13) y = tan θ(sin θ + cos θ)
(14) y = cosec x . cot x
(15) y = x sin x cos x
(16) y = e-x. log x
(17) y = (x2 +5) log(1+x)e-3x
(18) y = sin x°
(19) y = log10 x
(20) Draw the function f '(x) if f (x) = 2x2 − 5x + 3
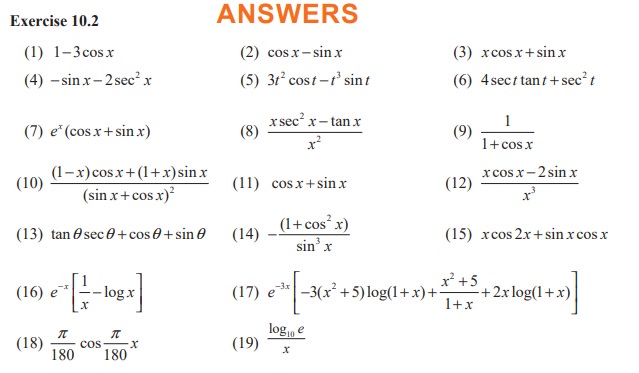
Related Topics