Exercise 10.5: Choose the correct answer

Differentiability and Methods of Differentiation - Differential Calculus (Mathematics)

Choose the correct or the most suitable answer from the given four alternatives.

(1)  d/ dx (2/π sin x° ) or 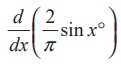 is 

(1) π/180 . cos x° 

(2) 1/90 . cos x° 

(3) π/90 . cos x° 

(4) 2/ π . cos x°

Ans: (2)

Solution

(2) If y = f (x² + 2) and f '(3) = 5, then dy/dx at x = 1 is 

(1) 5 

(2) 25 

(3) 15 

(4) 10

Ans: (4)

Solution

(3) If y = 1/4  u⁴ , u = 2/3  x³ + 5, then dy/dx is 

(1) 1/ 27 x² (2x³ +15)³ 

(2) 2/27 x (2x³ + 5)³ 

(3) 2/ 27  x² (2x³ +15)³ 

(4) 2/27  x (2x³ + 5)³ 

Ans: (3)

Solution

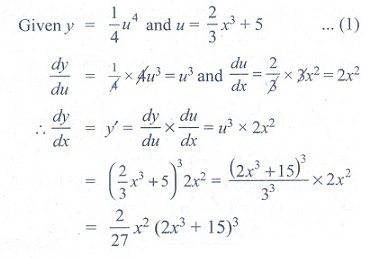
(4) If f (x) = x² − 3x , then the points at which f (x) = f '(x) are

(1) both positive integers 

(2) both negative integers

(3) both irrational 

(4) one rational and another irrational

Ans: (3)

Solution

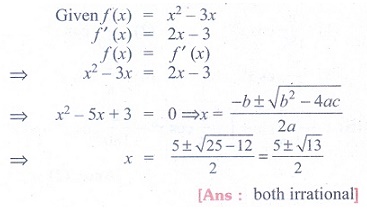
(5) If y = 1/ a − z , then dz/ dy is 

(1) (a − z)² 

(2) −( z − a)² 

(3) (z + a)² 

(4) − ( z + a)²

Ans: (1)

Solution

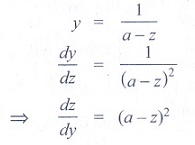
(6) If y = cos(sin x²), then dy/dx at x = √[π/2] is 

(1) - 2 

(2) 2 

(3) −2 √[π/2]

(4) 0

Ans: (4)

Solution

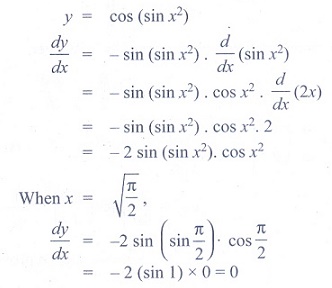
(7) If y = mx + c and f (0) = f '(0) = 1, then f (2) is

 (1) 1 

(2) 2 

(3) 3 

(4) - 3 

Ans: (3)

Solution

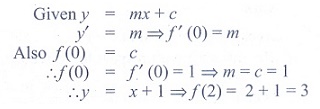
(8) If f (x) = x tan⁻¹x , then f '(1) is 

(1) 1+ π/4 

(2) 1/2 + π/4 

(3) 1/2 – π/4 

(4) 2 

Ans: (2)

Solution

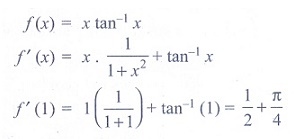
(9) d/ dx (e^{x +5logx}) is 

(1) e^x .x⁴ (x + 5) 

(2) e^x .x (x + 5) 

(3) e^x + 5/x

(4) e^x -  5/x

Ans: (1)

Solution

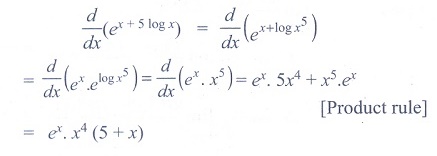
(10) If the derivative of (ax − 5)e^3x at x = 0 is -13, then the value of a is 

(1) 8 

(2) - 2 

(3) 5 

(4) 2 

Ans: (4)

Solution

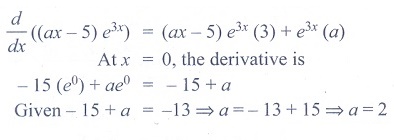
(11) 

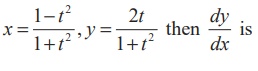
(1) −y /x

(2) y/x

(3) – x/y 

(4) x/y

Ans: (3)

Solution

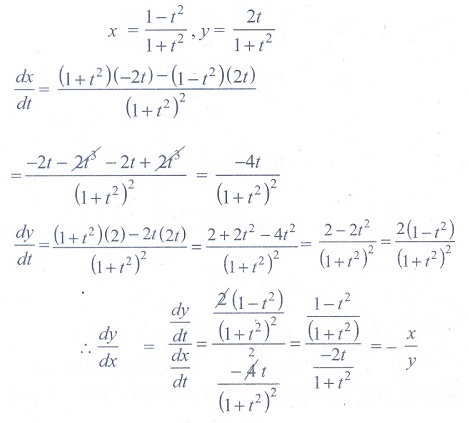
(12) If x = asinθ and y = bcosθ , then d²y/ d²x is 

(1) a/ b² sec²θ 

(2) – b/a sec²θ 

(3) –b/a² sec³θ 

(4) −b²/a²  sec³θ

Ans: (3)

Solution

(13) The differential coefficient of log₁₀x with respect to log_x10 is 

 (1) 1 

(2) −(log₁₀x)² 

(3) (log_x10)²

(4) x² /100

Ans: (2)

Solution

(14) If f (x) = x + 2, then f '( f (x)) at x = 4 is 

(1) 8 

(2) 1 

(3) 4 

(4) 5 

Ans: (2)

Solution

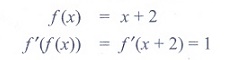
(15) If y = (1− x)²/ x² , then dy/ dx is 

(1) 2/x² + 2/x³ 

(2) −2/x² + 2/x³ 

(3) −2/x² − 2/x³ 

(4) −2/x² + 2/x³ 

Ans: (4)

Solution

(16) If pv = 81, then dp/dv at v = 9 is 

(1) 1 

(2) - 1 

(3) 2 

(4) -2 

Ans: (2)

Solution

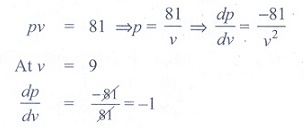
(17) If  f (x ) = , then the right hand derivative of f(x) at x = 2 is

(1) 0 

(2) 2 

(3) 3 

(4) 4 

Ans: (3)

Solution

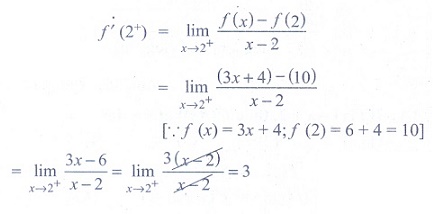
(18) It is given that f '(a) exists, then lim _{x →a} [xf (a ) − af (x)]/[ x − a] is 

(1) f (a ) − af '(a) 

(2) f '(a) 

(3) − f '(a) 

(4) f (a ) + af '(a)

Ans: (1)

Solution

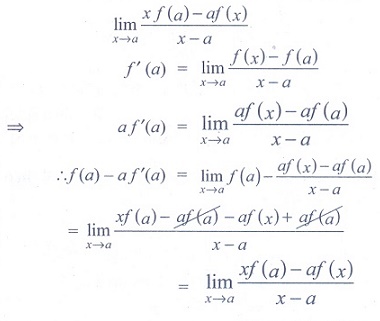
(19) If 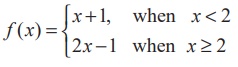 , then f '(2) is 

 (1) 0 

(2) 1 

(3) 2 

(4) does not exist

Ans: (4)

Solution

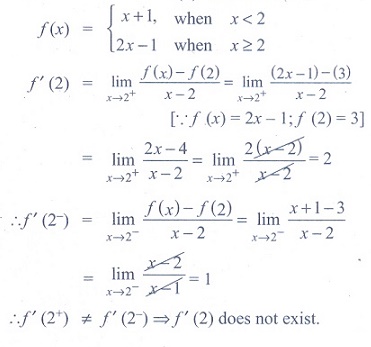
(20) If g (x) = (x² + 2x + 3) f (x) and f (0) = 5 and 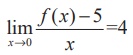, then g '(0) is

(1) 20 

(2) 14 

(3) 18 

(4) 12 

Ans: (2)

 (21) If , then at x = 3, f '(x) is 

(1) 1 

(2) - 1 

(3) 0 

(4) does not exist

Ans: (4)

Solution

(22) The derivative of f (x) = x | x | at x = −3 is 

(1) 6 

(2) - 6 

(3) does not exist 

(4) 0

Ans: (1)

Solution

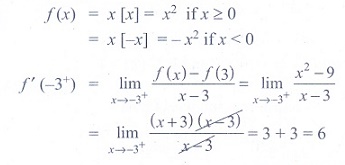
(23) If f (x) = 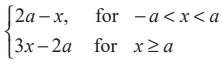, then which one of the following is true?

(1) f(x) is not differentiable at x = a 

(2) f(x) is discontinuous at x = a

 (3) f(x) is continuous for all x in R

(4) f(x) is differentiable for all x ≥ a

Ans: (1)

Solution

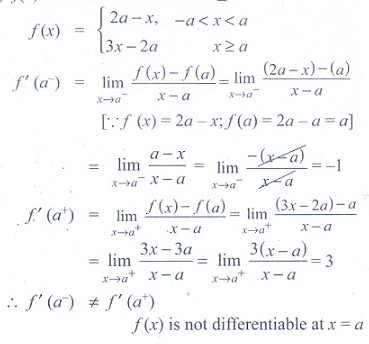
(24) If f (x) =  is differentiable at x = 1, then

 (1) a = 1/2 , b = −3/2 

(2) a = −1/2 , b = 3/2 

(3) a = − 1/2 , b = − 3/2 

(4) a = 1/2 , b = 3/2 

Ans: (3)

Solution

(25) The number of points in R in which the function f (x) =| x − 1| + | x − 3| + sin x is not differentiable, is 

(1) 3 

(2) 2 

(3) 1 

(4) 4 

Ans: (2)

Solution