The derivative of a Function - The concept of derivative

The derivative of a Function

We have now arrived at a crucial point in the study of calculus. The limit used to define the slope of a tangent line or the instantaneous velocity of a freely falling body is also used to define one of the two fundamental operations of calculus – differentiation.

Definition 10.2

Let f be defined on an open interval  I ⊆ R containing the point x0, and suppose that 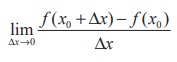exists. Then f is said to be differentiable at x0 and the derivative of f at x0, denoted by  f ′(x0 ) , is given by

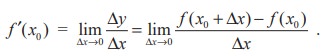
For all x for which this limit exists,

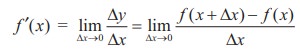
is a function of x.

Be sure you see that the derivative of a function of x is also a function of x. This “new” function gives the slope of the tangent line to the graph of f at the point (x, f(x)), provided the graph has a tangent line at this point.

The process of finding the derivative of a function is called differentiation. A function is differentiable at x if its derivative exists at x and is differentiable on an open interval (a, b) if it is differentiable at every point in (a, b).

In addition to f ′(x) , which is read as ‘f prime of x’ or ‘f dash of x’, other notations are used to denote the derivative of y = f(x). The most common notations are

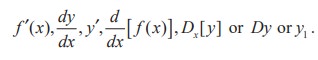
Herer d/dx or D is the differential operator.

The notation dy/dx is read as “derivative of y with respect to x” or simply “dy - dx”, or we should rather read it as “Dee y Dee x” or “Dee Dee x of y”. But it is cautioned that we should not regard dy/dx as the quotient dy ÷ dx and should not refer it as “dy by dx”. The symbol dy/dx is known as Leibnitz symbol.