Solved Example Problems| Mathematics - Higher order Derivatives | 11th Mathematics : UNIT 10 : Differential Calculus: Differentiability and Methods of Differentiation
Chapter: 11th Mathematics : UNIT 10 : Differential Calculus: Differentiability and Methods of Differentiation
Higher order Derivatives
Higher order Derivatives
If s = s(t) is the position function (displacement) of an object that moves in a straight line, we know that its first derivative has the simple physical interpretation as the velocity v(t) of the object as a function of time :
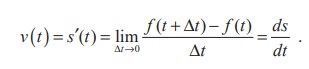
The instantaneous rate of change of velocity with respect to time is called the acceleration a(t) of the object. Then, the acceleration function is the derivative of the velocity function and is therefore the second derivative of the position function:
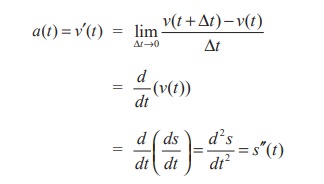
Thus, if f is a differentiable function of x, then its first derivative f ′(x) = 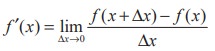 has a very simple geometrical interpretation as the slope of a tangent to the graph of y = f(x). Since f ′ is also a function of x, f ′ may have a derivative of its own, and if it exists, denoted by ( f ′)′ = f ′′ is,
has a very simple geometrical interpretation as the slope of a tangent to the graph of y = f(x). Since f ′ is also a function of x, f ′ may have a derivative of its own, and if it exists, denoted by ( f ′)′ = f ′′ is,
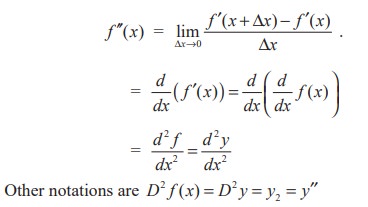
We can interpret a second derivative as a rate of change of a rate of change. But its geometrical interpretation is not so simple. However, there is a close connection exists between the second derivative f ′′(x) and the radius of curvature of the graph of y = f (x) which you will learn in higher classes.
Similarly, if f ′′ exists, it might or might not be differentiable. If it is, then the derivative of f ′′ is called third derivative of f and is denoted by

We can interpret the third derivative physically in case when the function is the position function f(t) of an object that moves along a straight line. Because s′′′ = (s′′)′ = a′(t) , the third derivative of the position function is the derivative of the acceleration function and is called the jerk:
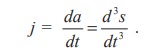
Thus, jerk is the rate of change of acceleration.
It is aptly named because a large jerk means a sudden change in acceleration, which causes an abrupt movement in a vehicle.
Example 10.31
Find y′, y′′ and y′′′ if y = x3 − 6x2 − 5x + 3.
Solution
We have, y = x3 − 6x2 − 5x + 3 and
y′= 3x2 − 12x – 5
y′′= 6x – 12
y′′′ = 6.
Example 10.32
Find y′′′ if y = 1/x .
Solution
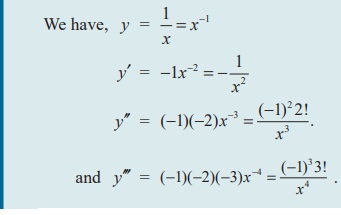
Example 10.33
Find f ′′ if f(x) = x cos x.
Solution
We have, f(x) = x cos x.
Now f ′(x) = - x sin x + cos x, and
f ′′(x) = - (x cos x + sin x) - sin x
= - x cos x - 2 sin x.
Example 10.34
Find y′′ if x4 + y4 = 16 .
Solution
We have x4 + y4 = 16 .
Differentiating implicitly, 4x3 + 4 y3 y′ = 0
Solving for y′ gives
y′ = x3/y3
To find y′′ we differentiate this expression for y′ using the quotient rule and remembering that y is a function of x.
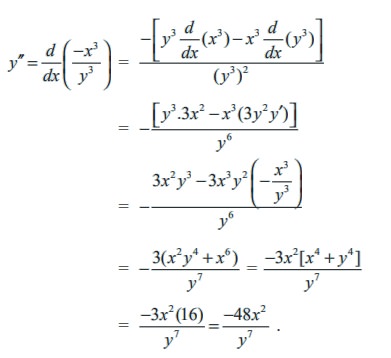
Example 10.35
Find the second order derivative if x and y are given by
x = a cos t
y = a sin t.
Solution
Differentiating the function implicitly with respect to x, we get

Example 10.36

EXERCISE 10.4
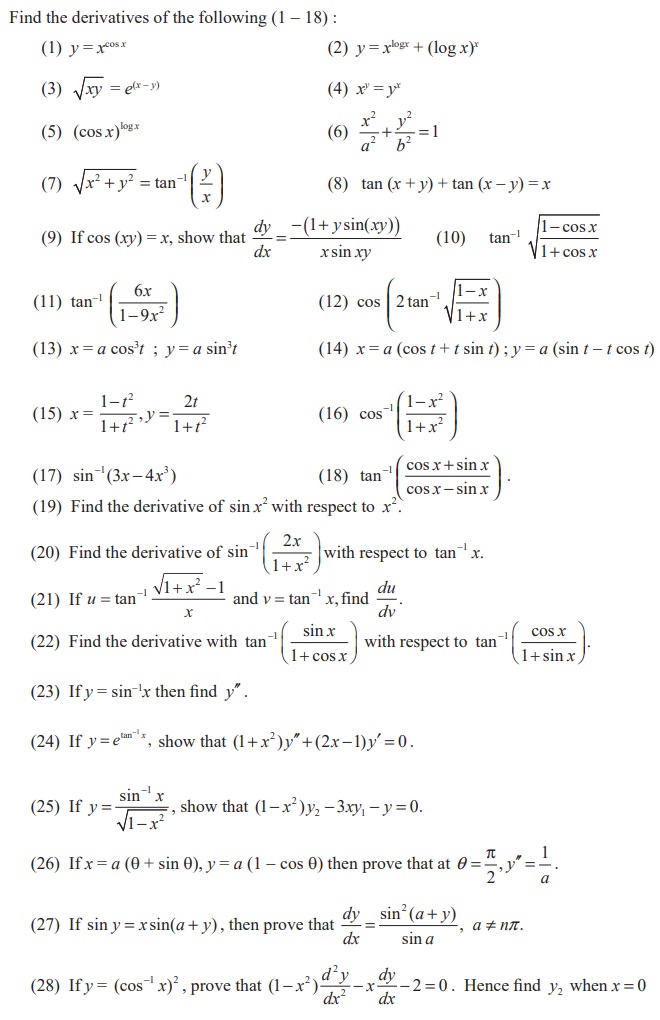

Related Topics