Derivatives of variables defined by parametric equations

Derivatives of variables defined by parametric equations

Consider the equations x = f(t), y = g(t).

These equations give a functional relationship between the variables x and y. Given the value of t in some domain [a, b], we can find x and y.

If two variables x and y are defined separately as a function of an intermediating (auxiliary) variable t, then the specification of a functional relationship between x and y is described as parametric and the auxiliary variable is known as parameter.

The operation of finding the direct connection between x and y without the presence of the auxiliary variable t is called elimination of the parameter. The question as to why should we deal with parametric equations is that two or more variables are reduced to a single variable, t.

For example, the equation of a circle with centre (0, 0) and radius r is x2 + y2 = r2 This equation describes the relationship between x and y and the equations

x = r cos t ; y = r sin t are parametric equations.

Conversely, if we eliminate t, we get x2 + y2 = r2

If we regard x as a function of y, then the derivative of x with respect to y is,

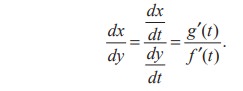
In the case of the circle, then dy/dx is the slope of the tangent to the circle namely