Logarithmic Differentiation

Logarithmic Differentiation

By using the rules for differentiation and the table of derivatives of the basic elementary functions, we can now find automatically the derivatives of any elementary function, except for one type, the simplest representative of which is the function y = xx. Such functions are described as power-exponential and include, in general, any function written as a power whose base and index both depend on the independent variable.

In order to find by the general rules the derivative of the power-exponential function y = xx, we take logarithms on both sides to get

log y = x log x, x > 0

Since this is an identity, the derivative of the left-hand side must be equal to the derivative of the right, we obtain by differentiating with respect to x (keeping in mind the fact that the left hand side is a function of function) :

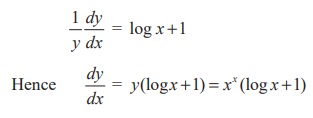
The operation consists of first taking the logarithm of the function f(x) (to base e) then differentiating is called logarithmic differentiation and its result

is called the logarithmic derivative of f(x).

The advantage in this method is that the calculation of derivatives of complicated functions involving products, quotients or powers can often be simplified by taking logarithms.

Steps in Logarithmic Differentiation

(1) Take natural logarithm on both sides of an equation y = f(x) and use the law of logarithms to simplify.

(2) Differentiate implicitly with respect to x.

(3) Solve the resulting equation for y′ .

In general there are four cases for exponents and bases.