Van der Waals Equation

Van der Waals Equation

J. D. Van der Waals made the first mathematical analysis of real gases. His treatment provides us an interpretation of real gas behaviour at the molecular level. He modified the ideal gas equation PV = nRT by introducing two correction factors, namely, pressure correction and volume correction.

Pressure Correction:

The pressure of a gas is directly proportional to the force created by the bombardment of molecules on the walls of the container. The speed of a molecule moving towards the wall of the container is reduced by the attractive forces exerted by its neighbours. Hence, the measured gas pressure is lower than the ideal pressure of the gas. Hence, van der Waals introduced a correction term to this effect.

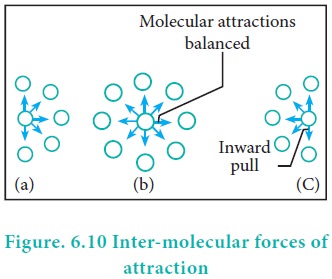
Van der Waals found out the forces of attraction experienced by a molecule near the wall are directly proportional to the square of the density of the gas.

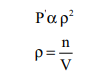
where n is the number of moles of gas and V is the volume of the container

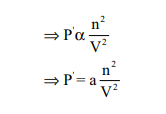
where a is proportionality constant and depends on the nature of gas

Therefore, 

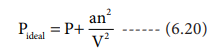
Volume Correction

As every individual molecule of a gas occupies a certain volume, the actual volume is less than the volume of the container, V. Van der Waals introduced a correction factor V' to this effect. Let us calculate the correction term by considering gas molecules as spheres.

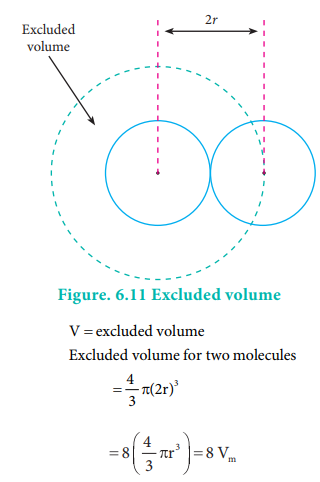
where vm  is a volume of a single molecule Excludeed volume for single molecule

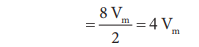
Excluded volume for n molecule = n(4Vm) = nb

Where b is van der waals constant whch is equal to 4 Vm

V' = nb 

Videal = V - nb  .... (6.21)

Replacing the corrected pressure and volume in the ideal gas equation PV=nRT we get the van der Waals equation of state for real gases as below,

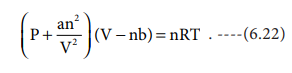
The constants a and b are van der Waals constants and their values vary with the nature of the gas. It is an approximate formula for the non-ideal gas.