Chapter: 11th Chemistry : UNIT 6 : Gaseous State
Derivation of critical constants from van der Waals constant
Derivation of critical constants from van der Waals constant:
The van der Waals equation for n moles is
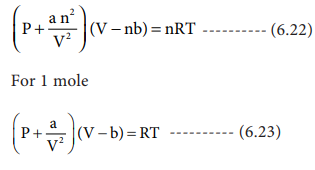
From the equation we can derive the values of critical constants Pc, Vc and Tc in terms of a and b, the van der Waals constants, On expanding the above equation
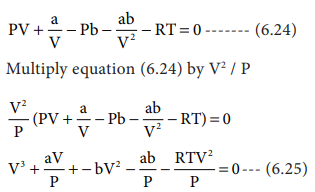
When the above equation is rearranged in powers of V
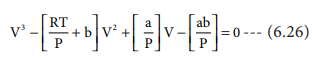
The equation (6.26) is a cubic equation in V. On solving this equation, we will get three solutions. At the critical point all these three solutions of V are equal to the critical volume VC. The pressure and temperature becomes Pc and Tc respectively
V = VC
V – VC = 0
(V – VC)3 = 0
V3 - 3VCV3 + 3VC2V - VC3 = 0 .......(6.27)
As equation (6.26) is identical with equation (6.27), we can equate the coefficients of V2, V and constant terms in (6.26) and (6.27).
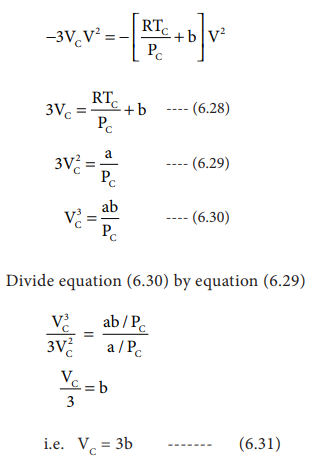
i.e. VC = 3b ------- (6.31)
when equation (6.31) is substituted in (6.29)
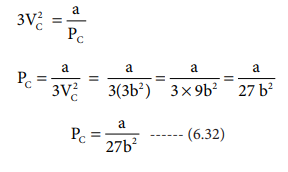
substituting the values of Vc and Pc in equation (6.28),
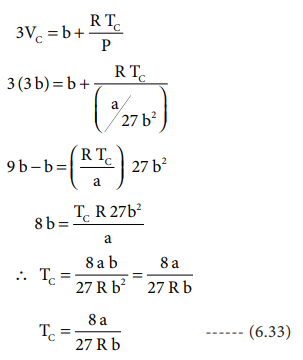
The critical constants can be calculated using the values of van der waals constant of a gas and vice versa.
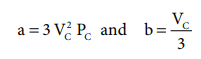
Related Topics