Chapter: 11th Chemistry : UNIT 6 : Gaseous State
Pressure-Volume isotherms of Carbon dioxide
Pressure-Volume
isotherms of Carbon dioxide
Andrew's isotherm
Thomas Andrew gave the first complete data on
pressure-volume-temperature of a substance in the gaseous and liquid states. He
plotted isotherms of carbon dioxide at different temperatures which is shown in
Figure. 6.12. From the plots we can infer the following.
At low temperature isotherms, for example, at 130 C as the
pressure increases, the volume decreases along AB and is a gas until the point
B is reached. At B, a liquid separates along the line BC, both the liquid and
gas co-exist and the pressure remains constant. At C, the gas is completely
converted into liquid. If the pressure is higher than at C, only the liquid is
compressed so, there is no significant change in the volume. The successive
isotherms shows similar trend with the shorter flat region. i.e. The volume range
in which the liquid and gas coexist becomes shorter. At the temperature of 31.1
0C the length of the shorter portion is reduced to zero at point P. In other
words, the CO2 gas is liquefied completely at this point. This
temperature is known as the liquefaction temperature or critical temperature of
CO2. At this point the pressure is 73 atm. Above this temperature CO2
remains as a gas at all pressure values. It is then proved that many real gases
behave in a similar manner to carbon dioxide.
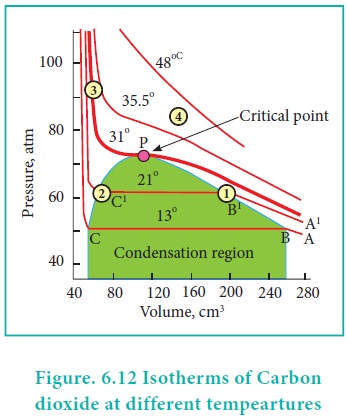
Though the nature of isotherm remains similar, the critical temperature, the corresponding pressure and volume are characteristics of a particular gas.
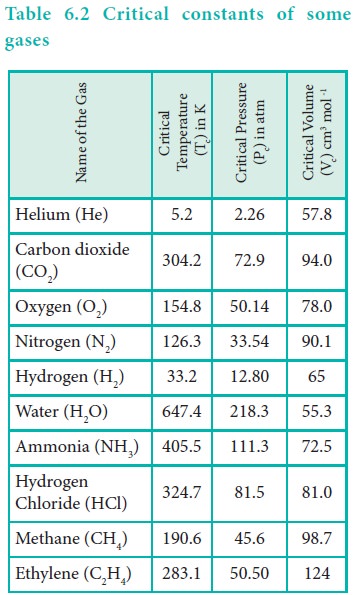
Now we can define the critical constants as follows.
Critical temperature (Tc) of a gas is defined as the temperature
above which it cannot be liquefied even at high pressure. Critical pressure (Pc)
of a gas is defined as the minimum pressure required to liquefy 1 mole of a gas
at its critical temperature. Critical volume (Vc) is defined as the
volume occupied by 1 mole of a gas at its critical temperature and critical
pressure. The critical constants of some common gases are given in Table 6.2
Derivation of critical constants from van der Waals constant:
The van der Waals equation for n moles is
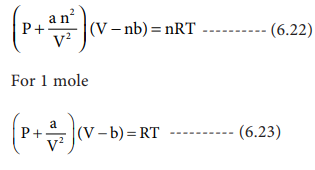
From the equation we can derive the values of critical
constants Pc, Vc and Tc in terms of a and b,
the van der Waals constants, On expanding the above equation
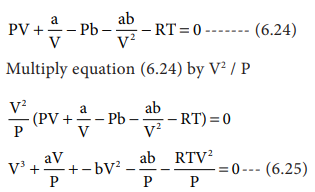
When the above equation is rearranged in powers of V
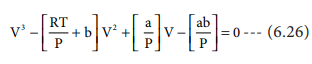
The equation (6.26) is a cubic equation in V. On solving
this equation, we will get three solutions. At the critical point all these
three solutions of V are equal to the critical volume VC. The
pressure and temperature becomes Pc and Tc respectively
V = VC
V – VC = 0
(V – VC)3 = 0
V3
- 3VCV3 + 3VC2V - VC3
= 0 .......(6.27)
As equation (6.26) is identical with equation (6.27), we
can equate the coefficients of V2, V and constant terms in (6.26)
and (6.27).
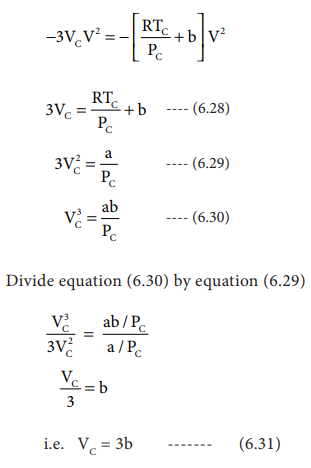
i.e. VC = 3b ------- (6.31)
when equation (6.31) is substituted in (6.29)

substituting the values of Vc and Pc
in equation (6.28),

The critical constants can be calculated using the values
of van der waals constant of a gas and vice versa.
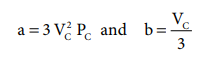
Related Topics