Brief Questions and Answers: Gaseous State (Chemistry)

Gaseous State (Chemistry)

Brief Questions and Answers

26. State Boyle's law.

At a given temperature, the volume occupied by a fixed mass of the gas is inversely proportional to its pressure

Boyle's law can be written as, V ∝ 1 / P

 (or) V = K (1/P)

 (or) PV = K

Q. A balloon filled with air at room temperature and cooled to a much lower temperature can be used as a model for Charle’s law 

27. Name two items that can serve as a model for Gay Lusaac’ law and explain.

1) Candle experiment (Air contains 1/5 of oxygen experiment)

2) Boiled Egg in a bottle experiment

28. Give the mathematical expression that relates gas volume and moles. Describe in words what the mathematical expression means.

● The mathematical expression that relates gas volume and moles is V ∝ n

● This mathematical expression is Avagadro hypothesis.(Avagadro Law). It states that, equal volume of all gases under the same conditions of temperature and pressure contains equal number of molecules.

29. What are ideal gases? In what way real gases differ from ideal gases.

● A gas which obeys the general gas equation (PV = nRT) under all conditions of temperature and pressure is called an ideal gas.

● The real gases differ from ideal gas only at high temperature and low pressure.

30. Can a Van der Waals gas with a=0 be liquefied? explain.

● Generally 'a' value is a measure of magnitude of the intermolecular force of attraction

● Since, a = 0 means, there is no intermolecular force of attraction exist between the gas molecules.

● So, Vander Waal gas with a = 0 cannot be liquefied.

31. Suppose there is a tiny sticky area on the wall of a container of gas. Molecules hitting this area stick there permanently. Is the pressure greater or less than on the ordinary area of walls?

● The pressure of the gas will be greater than on the ordinary area of walls.

● As per the postulates of kinetic theory of gases, pressure exerted by the gas is due to collision of its molecules on the wall of the container.

32. Explain the following observations

a) Aerated water bottles are kept under water during summer

b) Liquid ammonia bottle is cooled before opening the seal

c) The tyre of an automobile is inflated to slightly lesser pressure in summer than in winter

d) The size of a weather balloon becomes larger and larger as it ascends up into larger altitude

a) Aerated water bottles are kept under water during summer:

● Aerated water contains air/CO₂ dissolved in water (H₂O).

● The solubility of gas decreases with rise in temperature. (Henry's Law)

● Thus, amount of free gas in the bottle increases in summer, which may result in increase in pressure and ultimately explosion.

● To aviod this, they are kept under cold water.

b) Liquid ammonia bottle is cooled before opening the seal:

● At room temperature, the vapour pressure of liquid ammonia is very high.

● On cooling, the vapour pressure decreases (Gay Lussac's Law applies)

● Therefore, the liquid ammonia will not splash out of the bottle.

c) The tyre of an automobile is inflated to slightly lesser pressure in summer than in winter:

● In summer, due to high temperature, the average kinetic energy of air molecules inside the tube increases.

● Hence, the pressure on wall of the tube increases leads to burst of tyre.

● To aviod burst of tyre, it is better to have lesser pressure while inflate air in summer than in winter.

d) The size of a weather balloon becomes larger and larger as it ascends up into larger altitude:

● As we go to higher altitude, the atmospheric pressure decreases.

● Thus, the pressure outside the balloon decreases.

● To maintain equilibrium with external pressure, the gas inside expands to decrease its pressure. Hence, the size of the balloon increases.

33. Give suitable explanation for the following facts about gases.

a) Gases don’t settle at the bottom of a container

b) Gases diffuse through all the space available to them 

a) Gases don't settle at the bottom of a container:

● Gases are very less denser and also negligible intermolecular force of attraction between the particles of the gas. So, they are all free to move separately.

b) Gases diffuse through all the space available to them:

● The molecules in gases are far apart from each other due to negligible force of attraction between them.

● Hence, they have greater kinetic energy.

● So, particles move very fast and colloide with one another causing them to diffuse until they are evenly distributed throughout available space.

34. Suggest why there is no hydrogen (H2) in our atmosphere. Why does the moon have no atmosphere?

● Hydrogen is the lightest gas in the atmosphere. So, it rises up than the other gases which are heavier. More over hydrogen highly reactive towards oxygen. So, a major portion of hydrogen reacts and very less amount of it is present in the upper level of the atmosphere.

● Moon has no atmosphere because ‘g' value is small. The molecules of the atmospheric gases on surface of moon have greater thermal velocity (escape velocity than moon). That is why all the gaseous molecules have escaped and there is no atmosphere.

35. Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if

a) it is compressed to a smaller volume at constant temperature.

b) the temperature is raised at while keeping the volume constant

c) more gas is introduced into the same volume and at the same temperature

a) It is compressed to a smaller volume at constant temperature.

Gases deviates from ideal behavior because each molecule occupies definite volume.

b) The temperature is raised at while keeping the volume constant

As temperature is raised, kinetic energy of the molecule is greater. Hence, gas approaches ideal behavior.

c) More gas is introduced into the same volume and at the same temperature

More gas is introduced into the container, there is no room for the molecules to move around. So, each molecule occupies a definite volume. Hence, gas deviates from ideal behaviour.

36. Which of the following gases would you expect to deviate from ideal behaviour under conditions of low temperature F2, Cl2, or Br2? Explain.

Bromine deviates from ideal behaviour at low temperature. Because, molar mass of bromine is greater than chlorine and fluorine. So, kinetic energy of the molecules is less. Hence, it deviates from ideal behaviour.

37. Distinguish between diffusion and effusion.

Diffusion

The property of gas which involves the movement of the gas molecules through an another gas is called diffusion

Effusion

Effusion is another process in which gas escapes from a container through a very small hole.

38. Aerosol cans carry clear warning of heating of the can. Why?

Aersol can carry clear warning of heat of the can because of the high pressure that can develop upon heating. Hence, can will burst (or) explode if there is any residual hydrocarbon (or) if there is a naked flame nearby.

Q. When the driver of an automobile applies brake, the passengers are pushed toward the front of the car but a helium balloon is pushed toward back of the car. Upon forward acceleration the passengers are pushed toward the front of the car. Why? 

39. Would it be easier to drink water with a straw on the top of Mount Everest?

At the top of Mount Everest, air pressure is low. Hence, water is not pushed up the straw through your mouth. So, it is not easier to drink water.

40. Write the Van der Waals equation for a real gas. Explain the correction term for pressure and volume

The Vander Waals equation for real gas is

(P + [an²/V²] ) (V – nb) = nRT

Pressure Correction: For an ideal gas equation, P_idealV_ideal = nRT. But for a real gas the measured pressure is smaller than P_ideal due to attractive forces between real gas molecules. Therefore to make the pressure equivalent to P_ideal . We have to add some correction term to the measured pressure. The quantity

an² / V² is called Pressure Correction

Volume Correction: For an ideal gas P_ideal V_ideal = nRT. But for a real gas the measured volume is larger than V_ideal because real gas molecule occupies a definite volume. Therefore, to make the volume equivalent V_ideal some correction term must be subtracted from the measured volume. The quantity nb is called Volume Correction 

41. Derive the values of critical constants in terms of vander waals constants. [or] Derive the values of van der Waals equation constants in terms of critical constants.

The van der Waals equation for n moles is

 (P + [an²/V²]) (V – nb) = nRT      ............. (1)

For 1 mole

(P + [a/V²]) (V – b) = RT       ............. (2)

From the equation we can derive the values of critical constants Pc, Vc and Tc in terms of a and b, the van der Waals constants, On expanding the above equation

PV+ a/V − Pb − ab/V² − RT = 0      .... ...(3)

Multiply equation (3) by V² / P

V²/P (PV + a/V − Pb – ab/V² – RT ) = 0

V³ + aV/P – bV² – ab/P – RTV²/P = 0 ……..(4)

When the above equation is rearranged in powers of V

V³ + ([RT / P ] + b)V² + [a / p ]V – [ab / P ] = 0 ……..(5)

The equation (5) is a cubic equation in V. On solving this equation, we will get three solutions.

At the critical point all these three solutions of V are equal to the critical volume Vc. The pressure and temperature becomes Pc and Tc respectively

i.e., V = V_C

V − V_C = 0

(V − V_C)³ = 0

V³ − 3V_CV² + 3V_C²V − V_C³ = 0  ………..(6)

As equation (5) is identical with equation (6), we can equate the coefficients of V² , V and constant terms in (5) and (6).

−3VcV² = [ RT_c/P_c + b ] V²

3V_c = RT_c/P_c + b …………… (7)

3V_c² = a / V_c  …………… (8)

V_c³ = ab / P_c  ………..(9)

Divide equation (9) by equation (8)

V_c / 3V = ab/P_c / a/P

V_c³ / 3 = b

i.e. V _c = 3b ………………. (10)

when equation (10) is substituted in (8)

3V_c² = a/P_c

P_c = a/3V_c² = a / 3(3b²) = a / 3×9b² = a / 27b²

P_c = a / 27b² ………… (11)

Substituting the values of V_c and P_c, in equation (7),

3V_C = b + [ RT_C / P_C ]

3(3b) = b + [ RT_C 27b² / a]

RT_C 27b² / a = 9b − b

T_C = 8ba / 27Rb²

T_C = 8a / 27Rb ……………. (12)

The critical constants can be calculated using the values of van der waals constant of a gas and vice versa.

a = 3 V²_C P_C ;

b = V_c / 3

42. Why do astronauts have to wear protective suits when they are on the surface of moon?

On the surface of moon, there is no oxygen to breathe, no air pressure, extremely cold and filled with dangerous radiation. To avoid these difficulty, astronauts have to wear protective suit.

43. When ammonia combines with HCl, NH4Cl is formed as white dense fumes. Why do more fumes appear near HCl?

Ammonia diffuses faster than HCl due its lower molar mass. (According to Graham Law of diffusion) That why more fumes near HCl.

44. A sample of gas at 15 °C at 1 atm. has a volume of 2.58 dm3. When the temperature is raised to 38 °C at 1 atm does the volume of the gas increase? If so, calculate the final volume.

Answer:

T₁ = 15°C + 273

T₂ = 38 + 273

T₁ = 288 K

T₂ = 311 K

V₁ = 2.58 dm³

V₂ = ?

 (P = 1 atm constant)

Solution:

V₁ / T₁ = V₂ / T₂

V₂ = V₁/T₁ × T₂ = [2.58 dm³ / 288 K ] × 311 K

V₂ = 2.78 dm³

ie., volume increased from 2.58 dm³ to 2.78 dm³

45. A sample of gas has a volume of 8.5 dm3 at an unknown temperature. When the sample is submerged in ice water at 0 °C, its volume gets reduced to 6.37 dm3. What is its initial temperature?

Answer:

Given

V₁ = 8.5 dm³

V₂ = 6.37 dm³

T₁ = ?

T₂ = 0°

C = 273 K

Solution:

V₁ / T₁ = V₂ / T₂

V₁ × (T₂ / V₂) = T₁

= T₁

⇒ 8.5 dm³ × ( 273 K / 6.37 dm³ )

⇒ T₁ = 364.28 K

46. Of two samples of nitrogen gas, sample A contains 1.5 moles of nitrogen in a vessel of volume of 37.6 dm3 at 298K, and the sample B is in a vessel of volume 16.5 dm3 at 298K. Calculate the number of moles in sample B.

Answer:

Given

n_A = 1.5 mol

n_B = ?

V_A = 37.6 dm³

V_B = 16.5 dm³

(T = 298K constant)

Solution :

V_A / n_A = V_B / n_B

n_B = (n_A / V_A) V_B

= (1.5 mol / 37.6 dm³ ) × 16.5 dm³ = 0.66 mol

47. Sulphur hexafluoride is a colourless, odourless gas; calculate the pressure exerted by 1.82 moles of the gas in a steel vessel of volume 5.43 dm3 at 69.5 °C, assuming ideal gas behaviour

Answer:

[Alternative Answer] Answers are in doubt

Given:

n = 1.82 mole

V = 5.43 dm³

T = 69.5 + 273 = 342.5

P = ?

PV = nRT

Solution:

P = nRT / V

P = [1.82 × 0.0821 × 342.5] / 5.43

P = 9.425 atm

48. Argon is an inert gas used in light bulbs to retard the vaporization of the tungsten filament. A certain light bulb containing argon at 1.2 atm and 18°C is heated to 85°C at constant volume. Calculate its final pressure in atm.

Answer:

Given:

P₁ = 1.2 atm

T₁ = 18°C + 273 = 291K

T₂ = 85°C + 273 = 358 K

P₂ = ?

Solution:

P₁ / T₁ = P₂ / T₂

P₂ = (P₁/T₁ ) × T₂

= (1.2 atm / 291K) × 358 K

P₂ = 1.48 atm

49. A small bubble rises from the bottom of a lake where the temperature and pressure are 6°C and 4 atm. to the water surface, where the temperature is 25°C and pressure is 1 atm. Calculate the final volume in (mL) of the bubble, if its initial volume is 1.5 mL.

Answer:

Solution:

T₁ = 6°C + 273 = 279 K

P₁ = 4 atm

V₁ = 1.5 ml

T₂ = 25° C + 273 = 298 K

P₂ = 1 atm

V₂ = ?

P₁V₁ / T₁ = P₂V₂ / T₂

V₂ = [ P₁V₁ / T₁ ] × [T₂ / P₂]

= [ 4 atm × 1.5 ml × 298 K ] / [ 279 K × 1 atm ]

V₂ = 6.41 mol

50. Hydrochloric acid is treated with a metal to produce hydrogen gas. Suppose a student carries out this reaction and collects a volume of 154.4 × 10-3 dm3 of a gas at a pressure of 742 mm of Hg at a temperature of 298 K. What mass of hydrogen gas (in mg) did the student collect?

Answer:

Given:

V = 154.4 × 10⁻³ dm³,

P = 742 mm of Hg

T = 298 K

m = ?

n = PV / RT

= [ 742 mm Hg × 154.4 × 10⁻³L ] / [ 62 mm Hg LK⁻¹mol ⁻¹  × 298 K ]

= 0.006 mol

n = mass / Molar mass

Mass = n × Molar mass

= 0.006 × 2.016

= 0.0121g = 12.1 mg

51. It takes 192 sec for an unknown gas to diffuse through a porous wall and 84 sec for N2 gas to effuse at the same temperature and pressure. What is the molar mass of the unknown gas?

Answer:

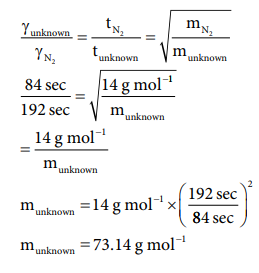
[Answers are in doubt ]

(84 / 192)² = 28 g mol⁻¹ / m_unknown

m_unknown = 28g mol⁻¹ × (192 sec / 84 sec )²

m_unknown = 146.28 mol⁻¹

52. A tank contains a mixture of 52.5 g of oxygen and 65.1 g of CO2 at 300 K the total pressure in the tanks is 9.21 atm. Calculate the partial pressure (in atm.) of each gas in the mixture.

Answer:

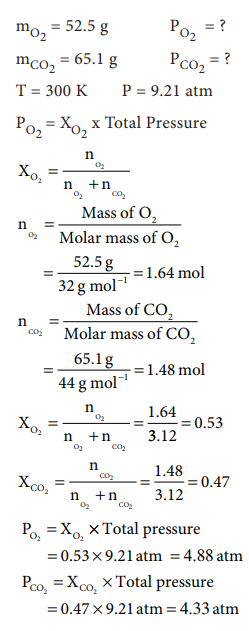
54. A combustible gas is stored in a metal tank at a pressure of 2.98 atm at 25 °C. The tank can withstand a maximum pressure of 12 atm after which it will explode. The building in which the tank has been stored catches fire. Now predict whether the tank will blow up first or start melting? (Melting point of the metal = 1100 K).

Answer:

Pressure of the gas in the tank at its melting point

T₁ = 298K;

P₁ = 2.98 atm ; 

T₂ = 1100 K;

P₂ = ?

Solution:

P₁/T₁ = P₂/T₂

⇒ P₂ = P₁ × (T₂ / T₁)

= (2.98 atm × 1100 K ) / 298 K = 11 atm

At 1100 K the pressure of the gas inside the tank will become 11 atm. Given that tank can withstand a maximum pressure of 12 atm, the tank will start melting first.