Chapter: Artificial Intelligence
Uninformed Search Strategies
UNINFORMED SEARCH STRATEGIES
ŌĆó
Uninformed strategies use only
the information available in the problem definition
ŌĆō Also known as blind searching
ŌĆō Uninformed search methods:
ŌĆó
Breadth-first search
ŌĆó
Uniform-cost search
ŌĆó
Depth-first search
ŌĆó
Depth-limited search
ŌĆó
Iterative deepening search
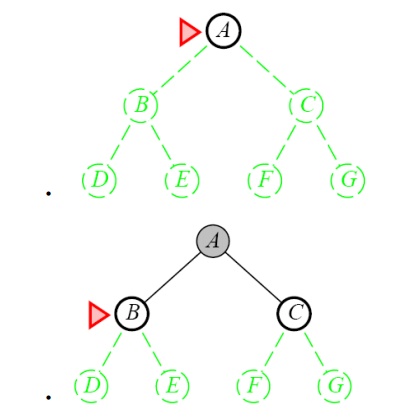
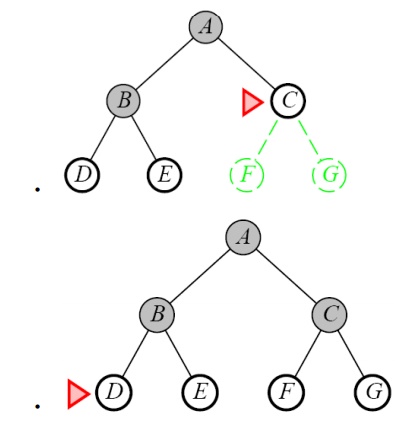
BREADTH-
FIRSTSEARCH
Definition:
The root
node is expanded first, and then all the nodes generated by the node are
expanded.
ŌĆó
Expand the shallowest
unexpanded node
ŌĆó
Place all new successors at the end of a FIFO queue
Implementation:
Properties of Breadth-First Search
ŌĆó
Complete
ŌĆō Yes if b (max branching factor) is finite
ŌĆó
Time
ŌĆō 1 + b + b2 + ŌĆ” + bd +
b(bd-1) = O(bd+1)
ŌĆō exponential in d
ŌĆó
Space
ŌĆō O(bd+1)
ŌĆō Keeps every node in memory
ŌĆō This is
the big problem; an agent that generates nodes at 10 MB/sec will produce
860 MB in
24 hours
ŌĆó
Optimal
ŌĆō Yes (if cost is 1 per step); not optimal in
general
Lessons from Breadth First Search
The
memory requirements are a bigger problem for breadth-first search than is
execution time
ŌĆó
Exponential-complexity search problems cannot be
solved by uniformed methods for any but the smallest instances
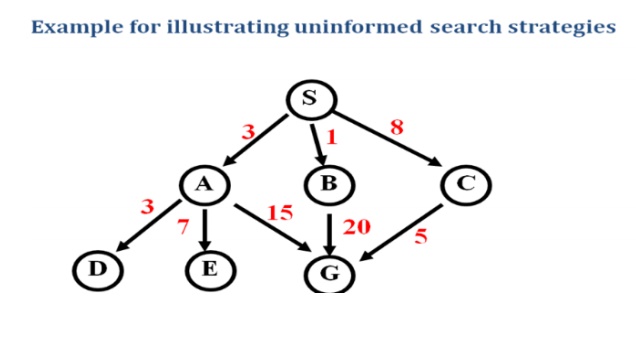
Ex: Route finding problem
Given:
Task: Find the route from S to G using BFS.
Step1:
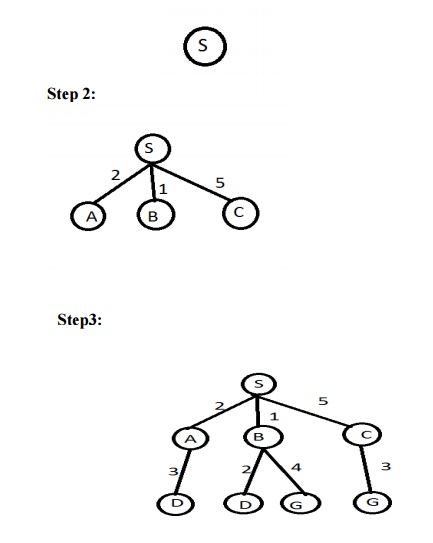

Answer : The path in the 2nd depth level that is SBG (or ) SCG.
Time complexity

DEPTH-FIRST SEARCH OR BACK TRACKING SEARCHING
Definition:
Expand
one node to the depth of the tree. If dead end occurs, backtracking is done to
the next immediate previous node for the nodes to be expanded
ŌĆó
Expand the deepest
unexpanded node
ŌĆó
Unexplored successors are placed on a stack until
fully explored
ŌĆó
Enqueue nodes on nodes in LIFO (last-in, first-out)
order. That is, nodes used as a stack data structure to order nodes.
ŌĆó
It has modest memory requirement.
ŌĆó
It needs to store only a single path from the root
to a leaf node, along with remaining unexpanded sibling nodes for each node on
a path
ŌĆó
Back track uses less memory.
Implementation:
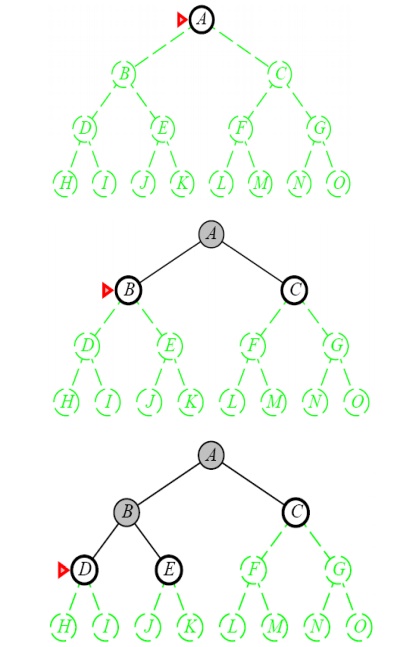
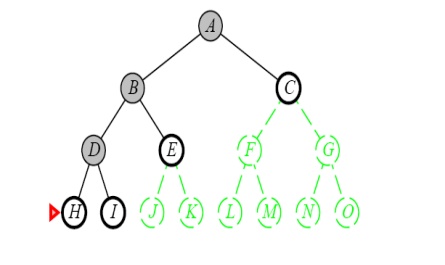
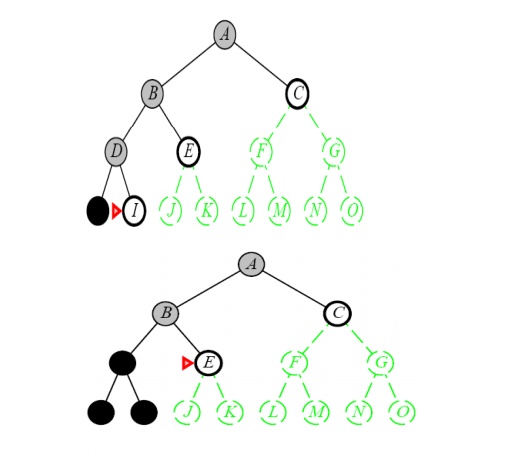
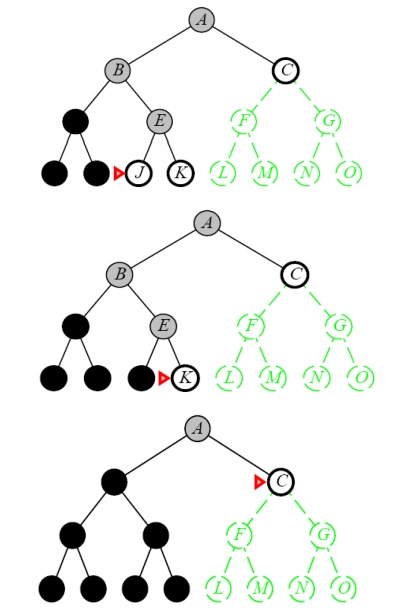
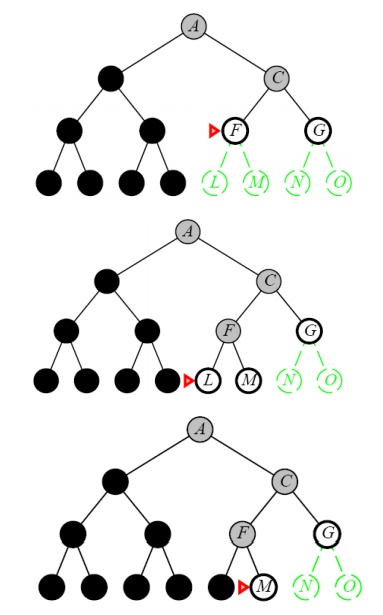
Properties of Depth-First Search
ŌĆó
Complete
ŌĆō No: fails in infinite-depth spaces, spaces
with loops
ŌĆó
Modify to avoid repeated spaces along path
ŌĆō Yes: in finite spaces
ŌĆó
Time
ŌĆō O(bm)
ŌĆō Not great if m is much larger than d
ŌĆō But if the solutions are dense, this may be
faster than breadth-first search
ŌĆó
Space
ŌĆō O(bm)ŌĆ”linear space
ŌĆó
Optimal
ŌĆō No
ŌĆó
When search hits a dead-end, can only back up one
level at a time even if the ŌĆ£problemŌĆØ occurs because of a bad operator choice
near the top of the tree. Hence, only does ŌĆ£chronological backtrackingŌĆØ
Advantage:
ŌĆó
If more than one solution exists or no of levels is
high then dfs is best because exploration is done only a small portion of the
white space.
Disadvantage:
ŌĆó
No guaranteed to find solution.
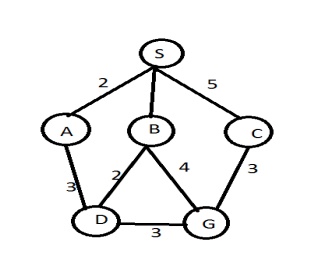
Example: Route finding problem
Given problem:
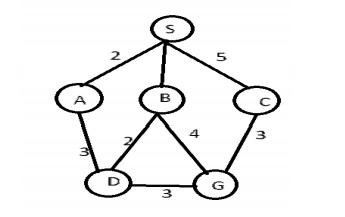
Task: Find a route between A to B
Step 1:
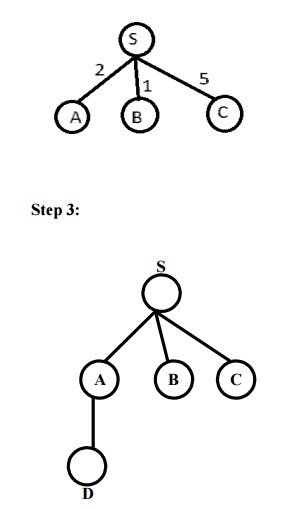
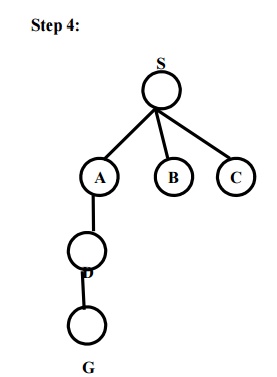
Answer: Path in 3rd level is SADG
DEPTH-LIMITED SEARCH
A cut off (Maximum level of the depth) is introduced in this search technique to overcome the disadvantage of Depth First Sea rch. The cut off value depends on the number o f states.DLS can be implemented as a simple modification to the general tree search algo rithm or the recursive DFS algorithm.DLS im poses a fixed depth limit on a dfs.
A variation of depth-first searc h that uses a
depth limit
ŌĆō Alleviates the problem of unbounded trees
ŌĆō Search to a predet ermined depth l (ŌĆ£ellŌĆØ)
ŌĆō Nodes at depth l h ave no successors
ŌĆó
Same as depth-first search if l = Ōł×
ŌĆó
Can terminate for failure and cutoff
ŌĆó
Two kinds of failure
Standard failure: indicates
no solution
Cut off: indicates no solution within the
depth limit

Properties of Depth-Limited Search
ŌĆó
Complete
ŌĆō Yes if l < d
ŌĆó
Time
ŌĆō N(IDS)=(d)b+(d-1)b┬▓+ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”..+(1)
ŌĆó
Space
ŌĆō O(bl)
ŌĆó
Optimal
ŌĆō No if l > d
Advantage:
ŌĆó
Cut off level is introduced in DFS Technique.
Disadvantage:
ŌĆó
No guarantee to find the optimal solution.
E.g.: Route finding problem
Given:
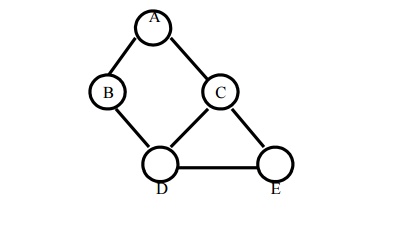
The
number of states in the given map is five. So it is possible to get the goal
state at the maximum depth of four. Therefore the cut off value is four.
Task: find a path from A to E.
Answer: Path = ABDE Depth=3
ITERATIVE DEEPENING SEARCH (OR) DEPTH-FIRST
ITERATIVE DEEPENING (DFID):
Definition:
ŌĆó
Iterative deepening depth-first search It is a
strategy that steps the issue of choosing the best path depth limit by trying
all possible depth limit
Uses
depth-first search
Finds the
best depth limit
Gradually increases the depth limit; 0, 1, 2, ŌĆ”
until a goal is found
Iterative Lengthening Search:
The idea
is to use increasing path-cost limit instead of increasing depth limits. The
resulting algorithm called iterative lengthening search.

Implementation:
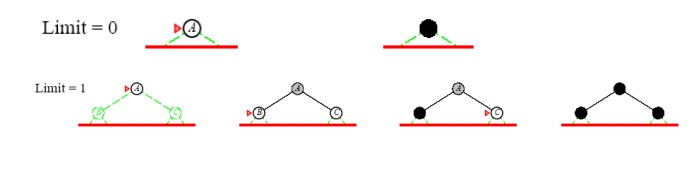
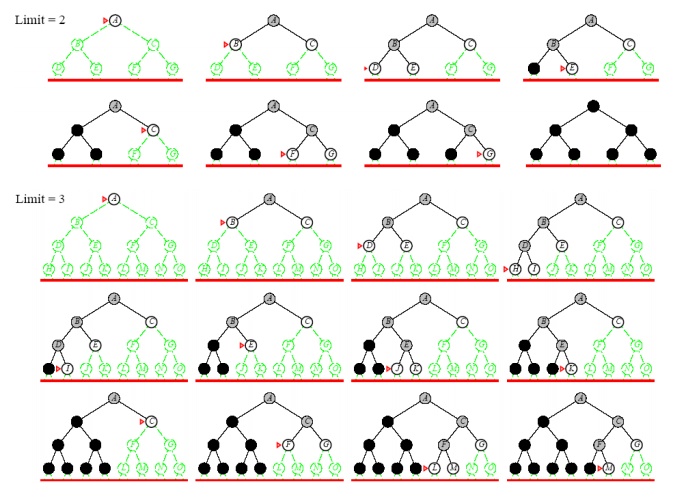
Properties of Iterative Deepening
Search:
ŌĆó
Complete
ŌĆō Yes
ŌĆó
Time : N(IDS)=(d)b+(d-1)b2+ŌĆ”ŌĆ”ŌĆ”ŌĆ”+(1)bd
ŌĆō O(bd)
ŌĆó
Space
ŌĆō O(bd)
ŌĆó
Optimal
ŌĆō Yes if step cost = 1
ŌĆō Can be modified to explore uniform cost tree
Advantages:
ŌĆó
This method is preferred for large state space and
when the depth of the search is not known.
ŌĆó
Memory requirements are modest.
ŌĆó
Like BFS it is complete
Disadvantages:
Many
states are expanded multiple times.
Lessons from Iterative Deepening Search
ŌĆó
If branching factor is b and solution is at depth
d, then nodes at depth d are generated once, nodes at depth d-1 are generated
twice, etc.
ŌĆō Hence bd + 2b(d-1) +
... + db <= bd / (1 - 1/b)2 = O(bd).
ŌĆō If b=4,
then worst case is 1.78 * 4d, i.e., 78% more nodes searched than
exist at depth d (in the worst case).
ŌĆó
Faster than BFS even though IDS generates repeated
states
ŌĆō BFS generates nodes up to level d+1
ŌĆō IDS only generates nodes up to level d
ŌĆó
In general, iterative deepening search is the
preferred uninformed search method when there is a large search space and the
depth of the solution is not known
Example: Route finding problem
Given:
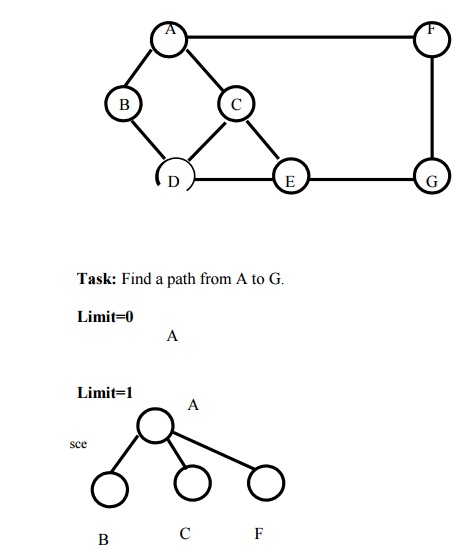
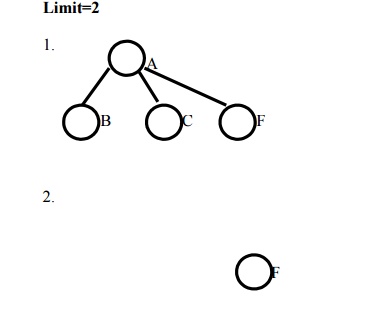
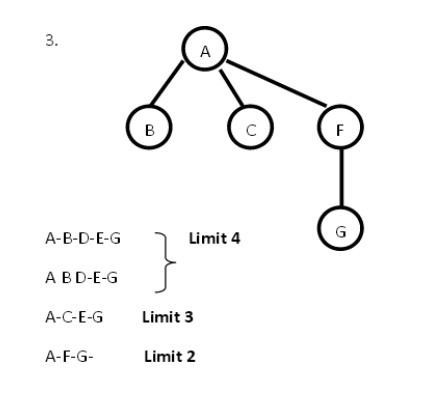
Answer: Since it is a IDS tree the lowest
depth limit (i.e.) A-F-G is selected as the solution path.
BI-DIRECTIONAL SEARCH
Definition:
It is a
strategy that simultaneously searches both the directions (i.e) forward from
the initial state and backward from the goal state and stops when the two
searches meet in the Middle.
ŌĆó
Alternate searching from the start state toward the
goal and from the goal state toward the start.
ŌĆó
Stop when the frontiers intersect.
ŌĆó
Works well only when there are unique start and
goal states.
ŌĆó
Requires the ability to generate ŌĆ£predecessorŌĆØ
states.
ŌĆó
Can (sometimes) lead to finding a solution more
quickly.
Properties of Bidirectional Search:
1.
Time Complexity: O(b d/2)
2.
Space Complexity: O(b d/2)
3.
Complete: Yes
4.
Optimal: Yes
Advantages:
Reduce
time complexity and space complexity
Disadvantages:
The space
requirement is the most significant weakness of bi-directional search.If two
searches do not meet at all, complexity arises in the search technique. In
backward search calculating predecessor is difficult task. If more than one
goal state exists then explicitly, multiple state searches are required.
COMPARING UNINFORMED SEARCH STRATEGIES
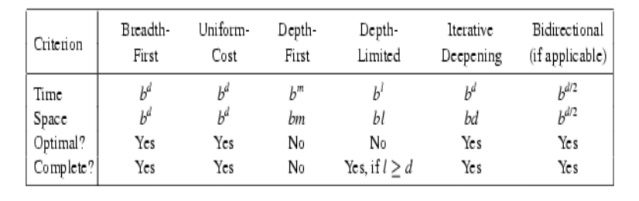
ŌĆó
Completeness
ŌĆō Will a solution always be found if one
exists?
ŌĆó
Time
ŌĆō How long does it take to find the solution?
ŌĆō Often
represented as the number of nodes searched
ŌĆó
Space
ŌĆō How much memory is needed to perform the
search?
ŌĆō Often represented as the maximum number of
nodes stored at once
ŌĆó
Optimal
ŌĆō Will the optimal (least cost) solution be
found?
ŌĆó
Time and
space complexity are measured in
ŌĆō b ŌĆō maximum branching factor of the search
tree
ŌĆō m ŌĆō maximum depth of the state space
ŌĆō d ŌĆō depth of the least cost solution
Related Topics